Xét các cặp tam giác sau đây, số cặp tam giác đồng dạng với nhau là:
(1) \(\Delta AEG\) và \(\Delta ABD\)
(2) \(\Delta ADF\) và \(\Delta ACE\)
(3) \(\Delta ABC\) và \(\Delta AEC\)
Trả lời bởi giáo viên
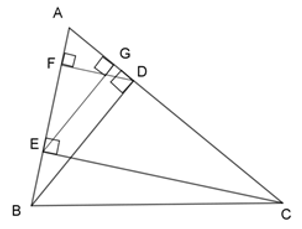
Xét \(\Delta ABD\) và \(\Delta AEG\), ta có:
\(BD \bot AC\) (BD là đường cao)
\(EG \bot AC\) (EG là đường cao)
\( \Rightarrow BD{\rm{//}}EG\)
Theo định lý Talet, ta có:
\(\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}\)
\( \Rightarrow \)\(\Delta \;AEG\backsim\Delta ABD\) (c - c -c) nên (1) đúng.
Tương tự ta cũng chứng minh được \(\Delta ADF \backsim \Delta ACE\) nên (2) đúng.
Dễ thấy (3) sai vì \(\dfrac{{AE}}{{AB}} \ne \dfrac{{AC}}{{AC}}\).
Vậy có hai cặp tam giác đồng dạng trong các cặp đã nêu.
Hướng dẫn giải:
+ Áp dụng định lý Talet để tìm ra tỉ lệ thức của các cạnh tỉ lệ trong \(2\) tam giác.
+ Từ đó suy ra 2 tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh.

