Hãy chọn câu sai. Hình chữ nhật có
Từ định nghĩa và tính chất hình chữ nhật ta có A, B, D đúng và C sai.
Tứ giác \(MNED\) là hình gì?
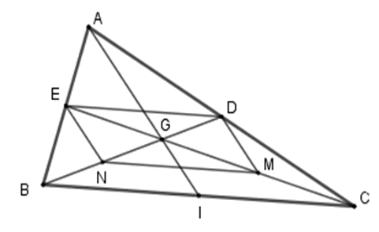
+ Xét tam giác \(ABC\) có \(E\) là trung điểm \(AB;\,D\) là trung điểm \(AC\) nên \(ED\) là đường trung bình của tam giác \(ABC \Rightarrow ED{\rm{//}}BC;\,ED = \dfrac{1}{2}BC\,\,\left( 1 \right)\) .
+ Xét tam giác \(GBC\) có \(N\) là trung điểm của \(GB;\,M\) là trung điểm \(GC\) nên \(MN\) là đường trung bình của tam giác \(GBC \Rightarrow MN{\rm{//}}BC;\,MN = \dfrac{1}{2}BC\,\,\left( 2 \right)\) .
Từ \(\left( 1 \right);\,\left( 2 \right)\, \Rightarrow MN{\rm{//}}ED;\,MN = ED\) nên tứ giác \(MNED\) là hình bình hành (dấu hiệu nhận biết).
Tứ giác $MNPQ$ là hình gì?
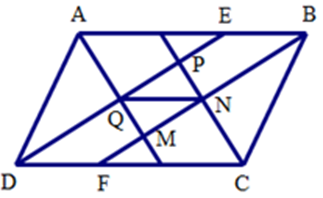
Ta có \(\widehat {QAD} + \widehat {QDA} = \dfrac{1}{2}\widehat {BAD} + \dfrac{1}{2}\widehat {ADC} = \dfrac{1}{2}\left( {\widehat {BAD} + \widehat {ADC}} \right)\) \( = \dfrac{1}{2}.180^\circ \) (do \(ABCD\) là hình bình hành)
Nên \(\widehat {QAD} + \widehat {QDA} = 90^\circ \Rightarrow \widehat {AQD} = 90^\circ \) (định lý tổng ba góc trong tam giác)
Nên \(AQ \bot DQ\). Suy ra \(\widehat {MQP} = {90^ \circ }\).
Tương tự : \(\widehat {NMQ} = \widehat {MNP} = {90^0}\)
Xét tứ giác MNPQ có \(\widehat {MQP} = \widehat {NMQ} = \widehat {MNP} = {90^0}\), do đó tứ giác $MNPQ$ là hình chữ nhật.
Hãy chọn câu sai:
+ Hình thang cân có một góc vuông là hình chữ nhật nên D đúng.
+ Hình bình hành có một góc vuông là hình chữ nhật nên B đúng.
+ Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật nên C đúng.
+ Hình thang có một góc vuông thì là hình thang vuông nên A sai.
Để \(MNED\) là hình chữ nhật thì tam giác \(ABC\) cần có điều kiện:
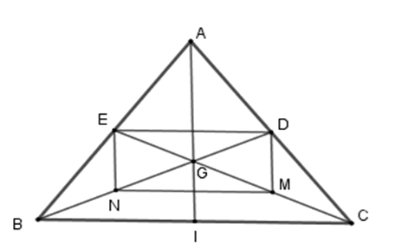
+ Xét tam giác \(ABG\) có \(EN\) là đường trung bình nên \(EN{\rm{//}}AG\) hay \(EN{\rm{//}}AI\).
+ Để hình bình hành \(MNED\) là hình chữ nhật thì \(\widehat {ENM} = 90^\circ \Rightarrow EN \bot MN\) . Mà \(MN{\rm{//}}BC\) (câu a) nên \(EN \bot BC\).
+ Lại có \(EN{\rm{//}}AI\) suy ra \(AI \bot BC\) .
Xét tam giác \(ABC\) có \(AI\) vừa là đường cao vừa là trung tuyến nên \(\Delta ABC\) cân tại \(A\) .
Tứ giác \(MNED\) là hình gì?

+ Xét tam giác \(ABC\) có \(E\) là trung điểm \(AB;\,D\) là trung điểm \(AC\) nên \(ED\) là đường trung bình của tam giác \(ABC \Rightarrow ED{\rm{//}}BC;\,ED = \dfrac{1}{2}BC\,\,\left( 1 \right)\) .
+ Xét tam giác \(GBC\) có \(N\) là trung điểm của \(GB;\,M\) là trung điểm \(GC\) nên \(MN\) là đường trung bình của tam giác \(GBC \Rightarrow MN{\rm{//}}BC;\,MN = \dfrac{1}{2}BC\,\,\left( 2 \right)\) .
Từ \(\left( 1 \right);\,\left( 2 \right)\, \Rightarrow MN{\rm{//}}ED;\,MN = ED\) nên tứ giác \(MNED\) là hình bình hành (dấu hiệu nhận biết).
Tứ giác \(MNED\) là hình gì?

+ Xét tam giác \(ABC\) có \(E\) là trung điểm \(AB;\,D\) là trung điểm \(AC\) nên \(ED\) là đường trung bình của tam giác \(ABC \Rightarrow ED{\rm{//}}BC;\,ED = \dfrac{1}{2}BC\,\,\left( 1 \right)\) .
+ Xét tam giác \(GBC\) có \(N\) là trung điểm của \(GB;\,M\) là trung điểm \(GC\) nên \(MN\) là đường trung bình của tam giác \(GBC \Rightarrow MN{\rm{//}}BC;\,MN = \dfrac{1}{2}BC\,\,\left( 2 \right)\) .
Từ \(\left( 1 \right);\,\left( 2 \right)\, \Rightarrow MN{\rm{//}}ED;\,MN = ED\) nên tứ giác \(MNED\) là hình bình hành (dấu hiệu nhận biết).
Tính độ dài đường chéo của hình chữ nhật$MNPQ$ theo \(a,\,b\) .
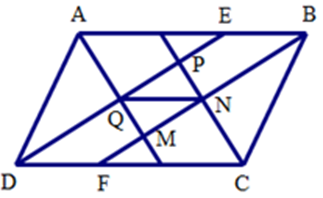
Gọi $E$ là giao điểm $PQ$ và $AB$ , $F$ là giao điểm của $MN$ và $CD$ . Tam giác $ADE$ có phân giác $AQ$ cũng là đường cao do đó tam giác cân tại $A$ , suy ra $DQ = QE = DE:2$ .
Tương tự tam giác $BCF$ cân tại$C$ , do đó $FN = BN = BF:2.$
Ta lại có $DEBF$ là hình bình hành (cặp cạnh đối song song), suy ra $DE = BF$ .
Suy ra $DQ = FN$ và $DQ$ //$FN$ . Vậy $DQNF$ là hình bình hành, từ đó $QN = DF = CD--CF$
Mà $CD = AB = a$ , $CF = CB = b$ , do đó: $QN = a-b$ .
Tứ giác $MNPQ$ là hình gì?

Ta có \(\widehat {QAD} + \widehat {QDA} = \dfrac{1}{2}\widehat {BAD} + \dfrac{1}{2}\widehat {ADC} = \dfrac{1}{2}\left( {\widehat {BAD} + \widehat {ADC}} \right)\) \( = \dfrac{1}{2}.180^\circ \) (do \(ABCD\) là hình bình hành)
Nên \(\widehat {QAD} + \widehat {QDA} = 90^\circ \Rightarrow \widehat {AQD} = 90^\circ \) (định lý tổng ba góc trong tam giác)
Nên \(AQ \bot DQ\). Suy ra \(\widehat {MQP} = {90^ \circ }\).
Tương tự : \(\widehat {NMQ} = \widehat {MNP} = {90^0}\)
Xét tứ giác MNPQ có \(\widehat {MQP} = \widehat {NMQ} = \widehat {MNP} = {90^0}\), do đó tứ giác $MNPQ$ là hình chữ nhật.
Tứ giác $MNPQ$ là hình gì?

Ta có \(\widehat {QAD} + \widehat {QDA} = \dfrac{1}{2}\widehat {BAD} + \dfrac{1}{2}\widehat {ADC} = \dfrac{1}{2}\left( {\widehat {BAD} + \widehat {ADC}} \right)\) \( = \dfrac{1}{2}.180^\circ \) (do \(ABCD\) là hình bình hành)
Nên \(\widehat {QAD} + \widehat {QDA} = 90^\circ \Rightarrow \widehat {AQD} = 90^\circ \) (định lý tổng ba góc trong tam giác)
Nên \(AQ \bot DQ\). Suy ra \(\widehat {MQP} = {90^ \circ }\).
Tương tự : \(\widehat {NMQ} = \widehat {MNP} = {90^0}\)
Xét tứ giác MNPQ có \(\widehat {MQP} = \widehat {NMQ} = \widehat {MNP} = {90^0}\), do đó tứ giác $MNPQ$ là hình chữ nhật.
Hãy chọn câu sai. Cho \(ABCD\) là hình chữ nhật có \(O\) là giao điểm hai đường chéo. Khi đó:
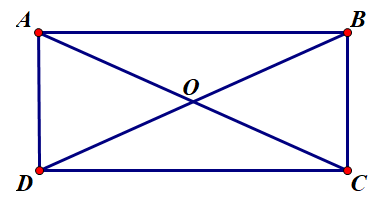
Vì \(ABCD\) là hình chữ nhật nên \(AB = DC;AD = BC;AC = BD\) và \(AC,BD\) cắt nhau tại trung điểm \(O\) của mỗi đường. Hay \(OA = OB = OC = OD\) nên A, B, C đúng, D sai.
Hãy chọn câu trả lời đúng. Hình thang cân \(ABCD\) là hình chữ nhật khi:
Hình thang cân có một góc vuông là hình chữ nhật nên hình thang cân \(ABCD\) có thêm \(\widehat {BCD} = 90^\circ \) thì nó sẽ là hình hữ nhật nên D đúng.
Chọn câu đúng: Cho tứ giác \(ABCD\) có:
Ta thấy: \(AD = BC,AD//BC,\,\widehat A = 90^\circ \) thì \(ABCD\) là hình bình hành có 1 góc vuông nên \(ABCD\) là hình chữ nhật.
Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng \(5\,cm\), \(12\,cm\) là:
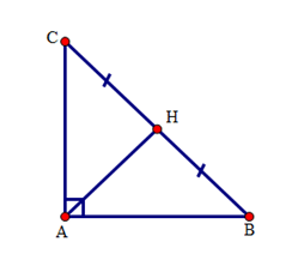
Áp dụng định lý Pytago cho tam giác \(ABC\) vuông tại \(A\) ta có:
\(B{C^2} = A{C^2} + A{B^2}\) hay \(B{C^2} = {5^2} + {12^2}\)\( \Rightarrow \)\(B{C^2} = 169\). Suy ra \(BC = 13\,\left( {cm} \right)\).
Do \(AH\) là đường trung tuyến ứng với cạnh huyền \(BC\) nên \(AH = BC:2 = 13:2 = 6,5\left( {cm} \right)\).
Cho tam giác \(ABC\) vuông cân tại \(A\), \(AC = 8\,cm\), điểm \(M\) thuộc cạnh \(BC\). Gọi \(D,E\) theo thứ tự là các chân đường vuông góc kẻ từ \(M\) đến \(AB,AC\). Chu vi của tứ giác \(ADME\) bằng:
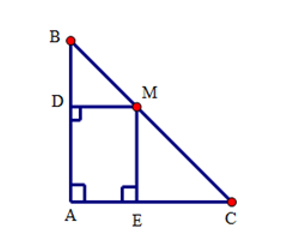
+ Xét tứ giác \(ADME\) có \(\widehat A = \widehat E = \widehat D = {90^ \circ }\) nên \(ADME\) là hình chữ nhật.
+ Xét tam giác \(DMB\) có \(\widehat B = {45^ \circ }\)(do tam giác \(ABC\) vuông cân) nên tam giác \(BDM\) vuông cân tại \(D\). Do đó \(DM = BD\).
+ Do \(ADME\) là hình chữ nhật nên chu vi \(ADME\) là:
\(\left( {AD + DM} \right). 2 = \left( {AD + BD} \right). 2 = 8. 2 = 16\left( {cm} \right)\).
Vậy chu vi \(ADME\) là \(16\,cm\).
Tính độ dài các cạnh \(AB,AL,AK\).
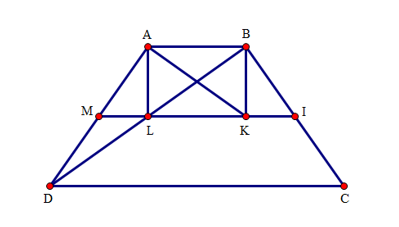
Theo câu trên ta có: \(AB = KL = {\rm{ }}6.\)
Áp dụng định lý Pitago cho tam giác vuông AML ta có:
\(A{L^2} = A{M^2} - M{L^2} = {5^2} - {3^2} = 16\)
Vậy \(AL = BK = 4.\)
Áp dụng định lý Pitago cho tam giác vuông AKL ta có:
\(A{K^2} = A{L^2} + L{K^2} = {4^2} + {6^2} = 16 + 36 = 52\).
Vậy \(AK = {\rm{ }}BL{\rm{ }} = \sqrt {52} \).
Vậy \(AB = 6;AL = 4;\,AK = \sqrt {52} \).
Tứ giác \(ABKL\) là hình gì?
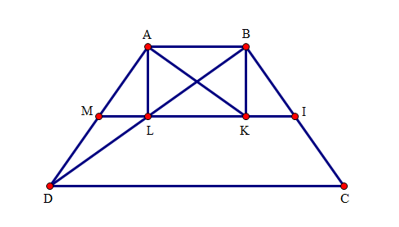
Xét tam giác ABD có : M, L lần lượt là trung điểm của AD, BD, do đó ML là đường trung bình của tam giác ABD. Suy ra \(ML//AB\) và \(ML = AB:2 = 3\). Vậy ML nằm trên đường trung bình MI của hình thang ABCD. (1)
Chứng minh tương tự ta có: IK là đường trung bình của tam giác ABC. Do đó, IK // AB và \(IK = AB:2 = 3.\) Vậy IK nằm trên đường trung bình MI của hình thang ABCD. (2)
Từ (1) và (2) suy ra: bốn điểm M, L, K, I nằm trên đường trung bình MI của hình thang ABCD.
Ta có: \(MI = \dfrac{1}{2}\left( {AB + CD} \right) = \dfrac{1}{2}\left( {6 + 18} \right) = 12\) (do MI là đường trung bình của hình thang ABCD)
Suy ra \(KL = MI-ML-KI = 12-3-3 = 6.\)
Xét tứ giác ABKL có: \(KL = AB\left( { = 6} \right);{\rm{ }}KL//AB.\) Do đó \(ABKL\) là hình bình hành.
Lại có: \(BL = \dfrac{1}{2}BD,AK = \dfrac{1}{2}AC\).
Mà \(AC = BD\) (đường chéo hình thang cân)
Suy ra \(AK = BL\).
Xét hình bình hành ABKL có \(AK = KL\) nên suy ra ABKL là hình chữ nhật.
Tứ giác \(ABKL\) là hình gì?

Xét tam giác ABD có : M, L lần lượt là trung điểm của AD, BD, do đó ML là đường trung bình của tam giác ABD. Suy ra \(ML//AB\) và \(ML = AB:2 = 3\). Vậy ML nằm trên đường trung bình MI của hình thang ABCD. (1)
Chứng minh tương tự ta có: IK là đường trung bình của tam giác ABC. Do đó, IK // AB và \(IK = AB:2 = 3.\) Vậy IK nằm trên đường trung bình MI của hình thang ABCD. (2)
Từ (1) và (2) suy ra: bốn điểm M, L, K, I nằm trên đường trung bình MI của hình thang ABCD.
Ta có: \(MI = \dfrac{1}{2}\left( {AB + CD} \right) = \dfrac{1}{2}\left( {6 + 18} \right) = 12\) (do MI là đường trung bình của hình thang ABCD)
Suy ra \(KL = MI-ML-KI = 12-3-3 = 6.\)
Xét tứ giác ABKL có: \(KL = AB\left( { = 6} \right);{\rm{ }}KL//AB.\) Do đó \(ABKL\) là hình bình hành.
Lại có: \(BL = \dfrac{1}{2}BD,AK = \dfrac{1}{2}AC\).
Mà \(AC = BD\) (đường chéo hình thang cân)
Suy ra \(AK = BL\).
Xét hình bình hành ABKL có \(AK = KL\) nên suy ra ABKL là hình chữ nhật.
Cho hình chữ nhật \(ABCD\) có \(AB = a;\,AD = b\). Cho \(M\), \(N\), \(P\), \(Q\) là các đỉnh của tứ giác \(MNPQ\) và lần lượt thuộc các cạnh \(AB\), \(BC\),\(CD,DA\). Tìm giá trị nhỏ nhất của chu vi tứ giác \(MNPQ\).
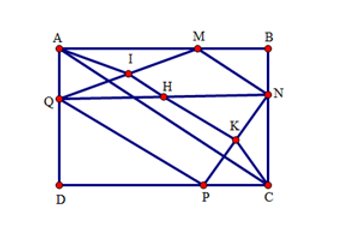
Gọi \(I,H,K\) lần lượt là trung điểm các đoạn \(QM,QN,PN\).
Xét tam giác \(AQM\) vuông tại \(A\) có \(AI\) là đường trung tuyến nên suy ra \(AI = \dfrac{1}{2}QM\).
\(IH\) là đường trung bình của tam giác \(QMN\) nên \(IH = \dfrac{1}{2}MN\), \(IH\) //\(MN\).
Tương tự: \(KC = \dfrac{1}{2}NP,HK = \dfrac{1}{2}PQ\), \(HK\) //\(PQ\).
Do đó \(AI{\rm{ }} + {\rm{ }}IH{\rm{ }} + {\rm{ }}HK{\rm{ }} + {\rm{ }}KC{\rm{ }} = \dfrac{1}{2}{P_{MNPQ}}\).
Mặt khác: nếu xét các điểm \(A,I,H,K,C\) ta có: \(AI{\rm{ }} + {\rm{ }}IH{\rm{ }} + {\rm{ }}HK{\rm{ }} + {\rm{ }}KC{\rm{ }} \ge AC\).
Do đó \({P_{MNPQ}} \ge 2AC\) (không đổi)
Dấu “=” xảy ra khi và chỉ khi \(A,I,H,K,C\) thẳng hàng theo thứ tự đó. Điều đó tương đương với \(MN\) //\(AC\) //\(QP\), \(QM\) //\(BD\) //\(NP\) hay \(MNPQ\) là hình bình hành.
Theo định lý Pytago cho tam giác \(ACB\) vuông tại \(A\) ta có:
\(A{C^2} = A{B^2} + B{C^2} = A{B^2} + A{D^2}\) \( = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \).
Vậy giá trị nhỏ nhất của chu vi \(MNPQ\) là \(2AC\) \( = 2\sqrt {{a^2} + {b^2}} \).
Tính độ dài nhỏ nhất của \(DE\) khi \(M\) di chuyển trên BC biết \(AB = 15cm;AC = 20cm.\)
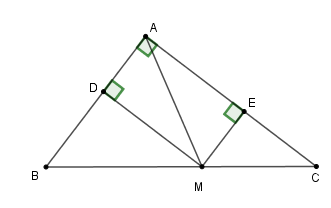
Theo \(DE\) nhỏ nhất khi \(M\) là hình chiếu của \(A\) trên \(BC.\) Khi đó \(DE = AM.\)
Xét tam giác \(ABC\), theo định lý Pyatgo ta có \(B{C^2} = A{B^2} + A{C^2} = 625 \Rightarrow BC = 25\).
Gọi \(BM = x\) thì \(MC = 25 - x\).
Xét tam giác \(AMB\) vuông tại \(M\), theo định lý Pytago ta có \(A{M^2} = A{B^2} - B{M^2} = {15^2} - {x^2} = 225 - {x^2}\) (1)
Xét tam giác \(AMC\) vuông tại \(M,\) theo định lý Pytago ta có \(A{M^2} = A{C^2} - M{C^2} = {20^2} - {\left( {25 - x} \right)^2}\) (2)
Từ (1) và (2) suy ra: \(225 - {x^2} = {20^2} - {\left( {25 - x} \right)^2}\)\( \Leftrightarrow 225 - {x^2} = 400 - \left( {625 - 50x + {x^2}} \right)\)\( \Leftrightarrow 50x = 450 \Leftrightarrow x = 9\).
Suy ra: \(A{M^2} = 225 - {x^2} = 225 - 81 = 144 \Rightarrow AM = 12\) suy ra \(DE = AM = 12cm\).
Vậy giá trị nhỏ nhất của \(DE\) là \(12cm.\)

