Trả lời bởi giáo viên
Đáp án đúng: a
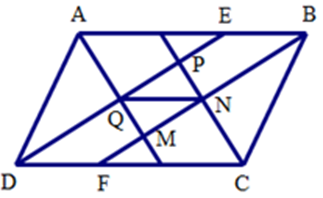
Ta có \(\widehat {QAD} + \widehat {QDA} = \dfrac{1}{2}\widehat {BAD} + \dfrac{1}{2}\widehat {ADC} = \dfrac{1}{2}\left( {\widehat {BAD} + \widehat {ADC}} \right)\) \( = \dfrac{1}{2}.180^\circ \) (do \(ABCD\) là hình bình hành)
Nên \(\widehat {QAD} + \widehat {QDA} = 90^\circ \Rightarrow \widehat {AQD} = 90^\circ \) (định lý tổng ba góc trong tam giác)
Nên \(AQ \bot DQ\). Suy ra \(\widehat {MQP} = {90^ \circ }\).
Tương tự : \(\widehat {NMQ} = \widehat {MNP} = {90^0}\)
Xét tứ giác MNPQ có \(\widehat {MQP} = \widehat {NMQ} = \widehat {MNP} = {90^0}\), do đó tứ giác $MNPQ$ là hình chữ nhật.
Hướng dẫn giải:
Ta chứng minh $QPNM$ là hình chữ nhật dựa vào dấu hiệu tứ giác có $3$ góc vuông là hình chữ nhật.

