Trả lời bởi giáo viên
Đáp án đúng: c
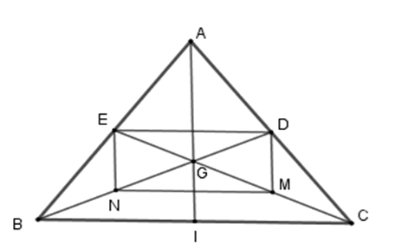
+ Xét tam giác \(ABG\) có \(EN\) là đường trung bình nên \(EN{\rm{//}}AG\) hay \(EN{\rm{//}}AI\).
+ Để hình bình hành \(MNED\) là hình chữ nhật thì \(\widehat {ENM} = 90^\circ \Rightarrow EN \bot MN\) . Mà \(MN{\rm{//}}BC\) (câu a) nên \(EN \bot BC\).
+ Lại có \(EN{\rm{//}}AI\) suy ra \(AI \bot BC\) .
Xét tam giác \(ABC\) có \(AI\) vừa là đường cao vừa là trung tuyến nên \(\Delta ABC\) cân tại \(A\) .
Hướng dẫn giải:
Bước 1: Chứng minh \(EN{\rm{//}}AI\) bằng tính chất đường trung bình.
Bước 2: Sử dụng dấu hiệu nhận biết “hình bình hành có một góc vuông là hình chữ nhật” để suy ra \(EN \bot NM\) .
Bước 3: Sử dụng quan hệ từ vuông góc đến song song để suy ra \(AI\) vừa là đường cao vừa là trung tuyến nên \(\Delta ABC\) cân tại \(A\) .

