Câu hỏi:
2 năm trước
Cho tam giác \(ABC\) vuông cân tại \(A\), \(AC = 8\,cm\), điểm \(M\) thuộc cạnh \(BC\). Gọi \(D,E\) theo thứ tự là các chân đường vuông góc kẻ từ \(M\) đến \(AB,AC\). Chu vi của tứ giác \(ADME\) bằng:
Trả lời bởi giáo viên
Đáp án đúng: a
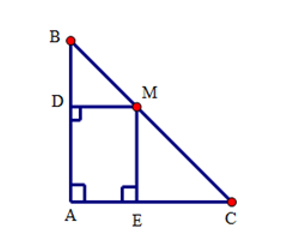
+ Xét tứ giác \(ADME\) có \(\widehat A = \widehat E = \widehat D = {90^ \circ }\) nên \(ADME\) là hình chữ nhật.
+ Xét tam giác \(DMB\) có \(\widehat B = {45^ \circ }\)(do tam giác \(ABC\) vuông cân) nên tam giác \(BDM\) vuông cân tại \(D\). Do đó \(DM = BD\).
+ Do \(ADME\) là hình chữ nhật nên chu vi \(ADME\) là:
\(\left( {AD + DM} \right). 2 = \left( {AD + BD} \right). 2 = 8. 2 = 16\left( {cm} \right)\).
Vậy chu vi \(ADME\) là \(16\,cm\).
Hướng dẫn giải:
Bước 1: Trước hết ta chứng minh \(ADME\) là hình chữ nhật dựa vào dấu hiệu tứ giác có \(3\) góc vuông là hình chữ nhật.
Bước 2: Chứng minh tam giác \(BDM\) vuông cân tại \(D\) để suy ra \(BD = DM\).
Bước 3: Tính chu vi \(ADME\) thông độ dài cạnh tam giác vuông cân.
