Cho hình chữ nhật \(ABCD\) có \(AB = a;\,AD = b\). Cho \(M\), \(N\), \(P\), \(Q\) là các đỉnh của tứ giác \(MNPQ\) và  lần lượt thuộc các cạnh \(AB\), \(BC\),\(CD,DA\). Tìm giá trị nhỏ nhất của chu vi tứ giác \(MNPQ\).

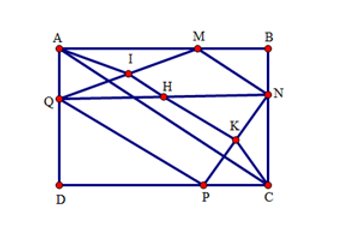
Gọi \(I,H,K\) lần lượt là trung điểm các đoạn \(QM,QN,PN\).

Xét tam giác \(AQM\) vuông tại \(A\) có \(AI\) là đường trung tuyến nên suy ra \(AI = \dfrac{1}{2}QM\).

\(IH\) là đường trung bình của tam giác \(QMN\) nên \(IH = \dfrac{1}{2}MN\), \(IH\) //\(MN\).

Tương tự: \(KC = \dfrac{1}{2}NP,HK = \dfrac{1}{2}PQ\), \(HK\) //\(PQ\).

Do đó \(AI{\rm{ }} + {\rm{ }}IH{\rm{ }} + {\rm{ }}HK{\rm{ }} + {\rm{ }}KC{\rm{ }} = \dfrac{1}{2}{P_{MNPQ}}\).

Mặt khác: nếu xét các điểm \(A,I,H,K,C\) ta có: \(AI{\rm{ }} + {\rm{ }}IH{\rm{ }} + {\rm{ }}HK{\rm{ }} + {\rm{ }}KC{\rm{ }} \ge AC\).

Do đó \({P_{MNPQ}} \ge 2AC\) (không đổi)

Dấu “=” xảy ra khi và chỉ khi \(A,I,H,K,C\) thẳng hàng theo thứ tự đó. Điều đó tương đương với \(MN\) //\(AC\) //\(QP\), \(QM\) //\(BD\) //\(NP\) hay \(MNPQ\) là hình bình hành.

Theo định lý Pytago cho tam giác \(ACB\) vuông tại \(A\) ta có:

\(A{C^2} = A{B^2} + B{C^2} = A{B^2} + A{D^2}\) \( = {a^2} + {b^2} \Rightarrow AC = \sqrt {{a^2} + {b^2}} \).

Vậy giá trị nhỏ nhất của chu vi \(MNPQ\) là \(2AC\) \( = 2\sqrt {{a^2} + {b^2}} \).