Tứ giác \(ABKL\) là hình gì?

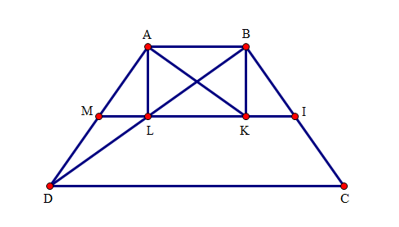
Xét tam giác ABD có : M, L lần lượt là trung điểm của AD, BD, do đó ML là đường trung bình của tam giác ABD. Suy ra \(ML//AB\) và \(ML = AB:2 = 3\). Vậy ML nằm trên đường trung bình MI của hình thang ABCD.  (1)

Chứng minh tương tự ta có: IK là đường trung bình của tam giác ABC. Do đó, IK // AB và \(IK = AB:2 = 3.\) Vậy IK nằm trên đường trung bình MI của hình thang ABCD. (2)

Từ (1) và (2) suy ra: bốn điểm M, L, K, I nằm trên đường trung bình MI của hình thang ABCD.

Ta có: \(MI = \dfrac{1}{2}\left( {AB + CD} \right) = \dfrac{1}{2}\left( {6 + 18} \right) = 12\) (do MI là đường trung bình của hình thang ABCD)

Suy ra \(KL = MI-ML-KI = 12-3-3 = 6.\)

Xét tứ giác ABKL có: \(KL = AB\left( { = 6} \right);{\rm{ }}KL//AB.\) Do đó \(ABKL\) là hình bình hành.

Lại có: \(BL = \dfrac{1}{2}BD,AK = \dfrac{1}{2}AC\).

Mà \(AC = BD\) (đường chéo hình thang cân)

Suy ra \(AK = BL\).

Xét hình bình hành ABKL có \(AK = KL\) nên suy ra ABKL là hình chữ nhật.