Dạng 1: Tính chu kì, tần số của con lắc lò xo
Sử dụng các công thức:
+ Tần số góc: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{g}{{\Delta {l_0}}}} = \frac{{2\pi }}{T} = 2\pi f\)
+ Chu kì: \(T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{\Delta {l_0}}}{g}} \)
+ Tần số: \(f = \frac{1}{{2\pi }}\sqrt {\frac{k}{m}} = \frac{1}{{2\pi }}\sqrt {\frac{g}{{\Delta {l_0}}}} \)
Với \(\Delta {l_0} = \frac{{mg}}{k}\) là độ biến dạng của lò xo khi vật ở vị trí cân bằng.
*Bài toán ghép vật
- Lò xo K gắn vật nặng m1 thì dao động với chu kì T1. Còn khi gắn vật nặng m2 thì dao động với chu kì T2. Chu kì dao động của vật khi gắn vật có khối lượng m = m1 + m2 là:
\({T^2} = T_1^2 + T_2^2\)
Tổng quát:
+ Chu kì dao động của vật khi gắn vật có khối lượng \(m = {m_1} + {m_2} + ... + {m_n}\) là:
\({T^2} = T_1^2 + T_2^2 + ... + T_n^2\)
+ Chu kì dao động của vật khi gắn vật có khối lượng m = a.m1 + b.m2 là:
\({T^2} = aT_1^2 + bT_2^2\)
- Lò xo K gắn vật nặng m1 thì dao động với chu kì f1. Còn khi gắn vật nặng m2 thì dao động với chu kì f2. Tần số dao động của vật khi gắn vật có khối lượng m = m1 + m2 là:
\(f = \frac{{{f_1}{f_2}}}{{\sqrt {f_1^2 + f_2^2} }}\)
Tổng quát:
+ Tần số dao động của vật khi gắn vật có khối lượng \(m = {m_1} + {m_2} + ... + {m_n}\) là:
\(\frac{1}{{{f^2}}} = \frac{1}{{f_1^2}} + \frac{1}{{f_2^2}} + ... + \frac{1}{{f_n^2}}\)
+ Tần số dao động của vật khi gắn vật có khối lượng m = a.m1 + b.m2 là:
\(\frac{1}{{{f^2}}} = \frac{{{a}}}{{f_1^2}} + \frac{{{b}}}{{f_2^2}}\)
Bài tập ví dụ:
Bài 1: Một con lắc lò xo nằm ngang có độ cứng k = 100 N/m được gắn vào vật nặng có khối lượng m = 0,1 kg. Kích thích cho vật dao động điều hòa, xác định chu kì của con lắc lò xo.
Hướng dẫn giải
Ta có:
\(\left\{ \begin{array}{l}m = 0,1kg\\k = 100N/m\end{array} \right. \Rightarrow T = 2\pi \sqrt {\frac{m}{k}} = 2\pi \sqrt {\frac{{0,1}}{{100}}} = 0,2 {\rm{s}}\)
Bài 2: Một lò xo có độ cứng là k. Khi gắn vậ m1 vào lò xo và cho dao động thì chu kì là 0,3 s. Khi gắn vật có khối lượng m2 vào lò xo trên và kích thích cho dao động thì nó dao động với chu kì là 0,4s. Hỏi nếu khi gắn vật có khối lượng m = 2m1 + 3m2 thì nó dao động với chu kì là bao nhiêu?
Hướng dẫn giải
Khi đó chu kì dao động của vật là:
\({T^2} = 2T_1^2 + 3T_2^2 \\\Leftrightarrow T = \sqrt {2T_1^2 + 3T_2^2} \\= \sqrt {2.0,{3^2} + 3.0,{4^2}} = 0,812s\)
Dạng 2: Chiều dài CLLX - lực đàn hồi, lực hồi phục của con lắc lò xo
1. Tính chiều dài của lò xo trong quá trình vật dao động
Gọi chiều dài tự nhiên của lò xo là l0.
- Khi con lắc lò xo nằm ngang:
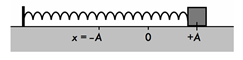
+ Lúc vật ở VTCB, lò xo không bị biến dạng,
+ Chiều dài cực đại của lò xo: \({l_{{\rm{max}}}} = {l_0} + A\)
+ Chiều dài cực tiểu của lò xo: \({l_{{\rm{min}}}} = {l_0} - A\)
+ Chiều dài ở li độ x: \(l = {l_0} + x\)
- Khi con lắc lò xo bố trí thẳng đứng hoặc nằm nghiêng một góc αvà treo ở dưới.
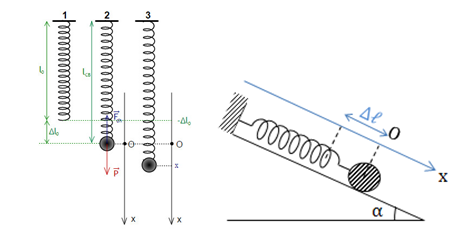
+ Độ biến dạng của lò xo khi vật ở VTCB:
- Con lắc lò xo treo thẳng đứng: \(\Delta {l_0} = \frac{{mg}}{k}\)
- Con lắc lò xo nằm nghiêng góc α: \(\Delta {l_0} = \frac{{mg\sin \alpha }}{k}\)
+ Chiều dài lò xo khi vật ở VTCB: \({l_{vtcb}} = {l_0} + \Delta l\)
+ Chiều dài ở li độ x: \(l = {l_0} + \Delta {l_0} + x\)
+ Chiều dài cực đại của lò xo: \({l_{{\rm{max}}}} = {l_0} + \Delta {l_0} + A\)
+ Chiều dài cực tiểu của lò xo: \({l_{{\rm{min}}}} = {l_0} + \Delta {l_0} - A\)
2. Lực kéo về
\(F{\rm{ }} = - {\rm{ }}kx{\rm{ }} = - {\rm{ }}m{\omega ^2}x\)
Đặc điểm:
* Là lực gây dao động cho vật.
* Luôn hướng về VTCB
* Biến thiên điều hoà cùng tần số với li độ
3. Lực đàn hồi - Lực hồi phục cực đại, cực tiểu.Có độ lớn \({F_{dh}} = {\rm{ }}k{x^*}\) (x* là độ biến dạng của lò xo)
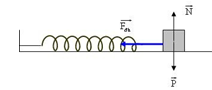
- Với con lắc lò xo nằm ngang thì lực kéo về và lực đàn hồi là một (vì tại VTCB lò xo không biến dạng)
- Với con lắc lò xo thẳng đứng hoặc đặt trên mặt phẳng nghiêng:
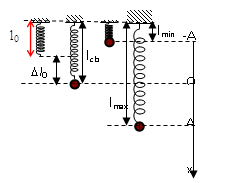
+ Độ lớn lực đàn hồi có biểu thức:
- \({F_{dh}} = {\rm{ }}k|\Delta {l_0} + {\rm{ }}x|\) với chiều dương hướng xuống
- \({F_{dh}} = k\left| {\Delta {l_0} - {\rm{ }}x} \right|\) với chiều dương hướng lên
+ Lực đàn hồi cực đại (lực kéo): \({F_{{\rm{max}}}} = k\left( {\Delta {l_0} + A} \right) = {F_{Km{\rm{ax}}}}\) (lúc vật ở vị trí thấp nhất)
+ Lực đàn hồi cực tiểu:
- Nếu\(A{\rm{ }} < \Delta {l_0} \to {F_{Min}} = {\rm{ }}k(\Delta {l_0} - {\rm{ }}A) = {F_{KMin}}\)
- Nếu \(A{\rm{ }} \ge \Delta {l_0} \to {F_{Min}} = 0\) (lúc vật đi qua vị trí lò xo không biến dạng)
+ Lực đẩy (lực nén) đàn hồi cực đại: ${F_{Nm{\rm{ax}}}} = k\left( {A - \Delta {l_0}} \right)$ (lúc vật ở vị trí cao nhất)
+ Lực đàn hồi, lực hồi phục:
- Lực đàn hồi:
\(\begin{array}{l}{F_{dh}} = k(\Delta l + x){\rm{ }}\\ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{F_{d{h_{{\rm{Max}}}}}} = k(\Delta l + A){\rm{ }}}\\{{F_{d{h_{\min }}}} = k(\Delta l - A){\rm{ khi }}\Delta l > A}\\{{F_{d{h_{\min }}}} = 0{\rm{ khi}}\Delta {\rm{l}} \le {\rm{A }}}\end{array}} \right.{\rm{ }}\end{array}\)
- Lực hồi phục: \({F_{hp}} = kx{\rm{ }} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{F_{h{p_{{\rm{Max}}}}}} = kA}\\{{F_{h{p_{\min }}}} = 0{\rm{ }}}\end{array}} \right.{\rm{ }}\)hay\({F_{hp}} = ma{\rm{ }} \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{F_{h{p_{{\rm{Max}}}}}} = m{\omega ^2}A}\\{{F_{h{p_{\min }}}} = 0{\rm{ }}}\end{array}} \right.\)
+ Lực hồi phục luôn hướng vào vị trí cân bằng.
Khi hệ dao động theo phương nằm ngang thì lực đàn hồi và lực hồi phục là như nhau ${F_{dh}} = {F_{hp}}$
Bài tập ví dụ: Một con lắc lò xo có chiều dài tự nhiên là 30 cm, độ cứng của lò xo là k = 10 N/m. Treo vật nặng có khối lượng m = 0,1 kg vào lò xo và kích thích cho lò xo dao động điều hòa theo phương thẳng đứng với biên độ A = 5cm. Xác định lực đàn hồi cực đại, cực tiểu của lò xo trong quá trình dao động của vật.
Hướng dẫn giải
Độ biến dạng của lò xo khi vật ở VTCB là:
\(\Delta {l_0} = \frac{{mg}}{k} = \frac{{0,1.10}}{{10}} = 0,1m\)
Lực đàn hồi cực đại:
\({F_{\max }} = k\left( {\Delta {l_0} + A} \right) = 10.\left( {0,1 + 0,05} \right) = 1,5N\)
Lực đàn hồi cực tiểu:
\({F_{\min }} = k\left( {\Delta l - A} \right) = 10.\left( {0,1 - 0,05} \right) = 0,5N\)
Dạng 3. Bài tập năng lượng của con lắc lò xo
Phương pháp
Cho một con lắc lò xo có độ cứng k, vật có khối lượng m, dao động điều hòa với phương trình : \(x = Ac{\rm{os(}}\omega {\rm{t + }}\varphi {\rm{)}}\) và có vận tốc: \(v = - A\omega \sin (\omega t + \varphi )\).
- Cơ năng: \(W = {W_d} + {W_t} = \dfrac{1}{2}m{v^2} + \dfrac{1}{2}k{x^2} = \dfrac{1}{2}m{\omega ^2}{A^2} = \dfrac{1}{2}k{A^2}\)
- Thế năng:
\(\begin{array}{l}{W_t} = \dfrac{1}{2}k{x^2} = \dfrac{1}{2}k{A^2}{\rm{co}}{{\rm{s}}^2}(\omega t + \varphi )\\ = W - {W_d} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}m{v^2}\end{array}\)
- Động năng:
\(\begin{array}{l}{W_d} = \dfrac{1}{2}m{v^2} = \dfrac{1}{2}m{\omega ^2}{A^2}{\sin ^2}(\omega t + \varphi )\\ = W - {W_t} = \dfrac{1}{2}k{A^2} - \dfrac{1}{2}k{x^2}\end{array}\)
- Đồ thị dao động:
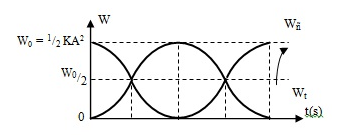
Nhận xét:
- Cơ năng được bảo toàn và tỉ lệ với bình phương biên độ.
- Vị trí thế năng cực đại thì động năng cực tiểu và ngược lại.
- Động năng và thế năng của vật biến thiên điều hòa với cùng tần số góc \(2ω\), tần số \(2f\) và chu kì \(\dfrac{T}{2}\).
- Trong 1 chu kì: có 4 lần động năng bằng thế năng. Khoảng thời gian ngắn nhất giữa hai lần động năng bằng thế năng là \(\dfrac{T}{4}\).
- Xác định vận tốc- li độ:
- Vận tốc: \({W_d} = \dfrac{1}{2}m{v^2} \to v = \pm \sqrt {\dfrac{{2{W_d}}}{m}} \)
- Li độ: \({W_t} = \dfrac{1}{2}k{x^2} \to x = \pm \sqrt {\dfrac{{2{W_t}}}{k}} \)
- Khi biết thế năng tại vị trí có li độ x gấp n lần động năng của vật: Wt = nWđ
\(\left\{ \begin{array}{l}{W_t} = n{W_d}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{n}{{n + 1}}W\\{W_d} = \dfrac{1}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm A\sqrt {\dfrac{n}{{n + 1}}} \\v = \pm \dfrac{{A\omega }}{{\sqrt {n + 1} }}\end{array} \right.\)
- Khi biết động năng tại vị trí có li độ x gấp n lần thế năng của vật: Wđ = nWt
\(\left\{ \begin{array}{l}{W_d} = n{W_t}\\W = {W_t} + {W_d}\end{array} \right. \to \left\{ \begin{array}{l}{W_t} = \dfrac{1}{{n + 1}}W\\{W_d} = \dfrac{n}{{n + 1}}W\end{array} \right. \to \left\{ \begin{array}{l}x = \pm \dfrac{A}{{\sqrt {n + 1} }}\\v = \pm A\omega \sqrt {\dfrac{n}{{n + 1}}} \end{array} \right.\)
Dạng 4. Tính thời gian lò xo nén hay giãn trong một chu kì
Phương pháp:
1. Con lắc lò xo nằm ngang:
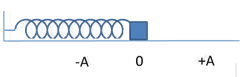
Thời gian lò xo giãn bằng thời gian lò xo nén
2. Con lắc lò xo treo thẳng đứng:
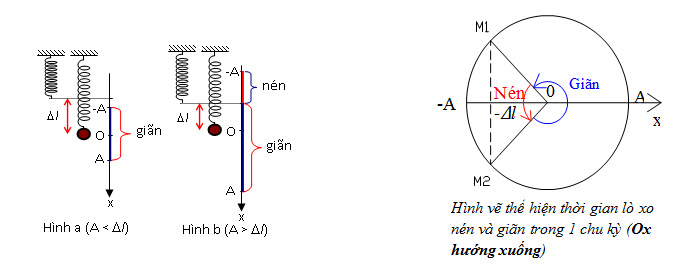
+ Khi \(A < \Delta {l_0}\) : Trong quá trình dao động, lò xo chỉ bị giãn mà không có nén => Thời gian lò xo giãn = T, thời gian lò xo nén = 0
+ Khi \(A > \Delta {l_0}\) :
- Thời gian lò xo nén 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\) đến \({x_2} = - A\) là : \(\Delta t = 2\frac{\alpha }{\omega }\) trong đó: \({\rm{cos}}\alpha {\rm{ = }}\frac{{\Delta {l_0}}}{A}\)
- Thời gian lò xo giãn 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\)đến \({x_2} = - A\) là: \(T - \Delta t\)
Trong một dao động (một chu kỳ) lò xo nén 2 lần và giãn 2 lần
3. Con lắc lò xo nằm nghiêng:
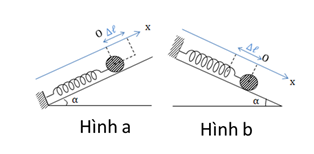
+ Khi \(A{\rm{ }} < \Delta {l_0}\) :
- Đầu cố định ở trên (Hình b): Trong quá trình dao động, lò xo chỉ bị giãn mà không có nén => Thời gian lò xo giãn = T, thời gian lò xo nén = 0
- Đầu cố định ở dưới (Hình a): Trong quá trình dao động, lò xo chỉ bị nén mà không có giãn => Thời gian lò xo giãn = 0, thời gian lò xo nén = T
+ Khi \(A{\rm{ }} > \Delta {l_0}\) :
- Thời gian lò xo nén 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\)đến \({x_2} = - A\)là : \(\Delta t = 2\frac{\alpha }{\omega }\) trong đó: \({\rm{cos}}\alpha {\rm{ = }}\frac{{\Delta {l_0}}}{A}\)
- Thời gian lò xo giãn 1 lần là thời gian ngắn nhất để vật đi từ vị trí \({x_1} = - \Delta {l_0}\)đến \({x_2} = - A\)là: T-∆t
Trong một dao động (một chu kỳ) lò xo nén 2 lần và giãn 2 lần
Dạng 5. Bài toán va chạm
1. Va chạm theo phương ngang

Vật m chuyển động với vận tốc v0 đến va chạm vào vật M đang đứng yên.
- Va chạm mềm: \(m{v_0} = (m + M)V \Rightarrow V = \frac{1}{{1 + \frac{M}{m}}}{v_0}\)
V: vận tốc của hệ hai vật M+m ở vị trí cân bằng
Nếu sau va chạm cả hai vật dao động điều hòa thì tần số và biên độ dao động của con lắc lò xo:
\(\omega = \sqrt {\frac{k}{{m + M}}} ,A = \frac{V}{\omega }\)
- Va chạm đàn hồi: \(\left\{ \begin{array}{l}m{v_0} = mv + MV\\\frac{1}{2}mv_0^2 = \frac{1}{2}m{v^2} + \frac{1}{2}M{V^2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}V = \frac{2}{{1 + \frac{M}{m}}}{v_0}\\v = \frac{{1 - \frac{M}{m}}}{{1 + \frac{M}{m}}}{v_0}\end{array} \right.\)
V: vận tốc của M ở vị trí cân bằng
Nếu sau va chạm M dao động điều hòa: \(\omega = \sqrt {\frac{k}{M}} ,A = \frac{V}{\omega }\)
2. Va chạm theo phương thẳng đứng
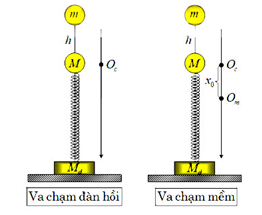
Tốc độ của m ngay trước va chạm: \({v_0} = \sqrt {2gh} \)
- Va chạm mềm:
+ Vị trí cân bằng mới thấp hơn vị trí cân bằng cũ đoạn \({x_0} = \frac{{mg}}{k}\)
+ Vận tốc của hệ sau va chạm: \(V = \frac{{m{v_0}}}{{m + M}}\)
+Biên độ sau va chạm: \(A = \sqrt {x_0^2 + \frac{{{V^2}}}{{{\omega ^2}}}} \)
- Xảy ra va chạm đúng lúc vật đến vị trí cao nhất thì sau va chạm: vật có li độ so với VTCB mới (A0+x0), biên độ mới \(A = \sqrt {{{({A_0} + {x_0})}^2} + \frac{{{V^2}}}{{{\omega ^2}}}} \)
- Xảy ra va chạm đúng lúc vật đến vị trí thấp nhất thì sau va chạm: vật có li độ so với VTCB mới (A0-x0), biên độ mới \(A = \sqrt {{{({A_0} - {x_0})}^2} + \frac{{{V^2}}}{{{\omega ^2}}}} \)
- Va chạm đàn hồi:
+ \(V = \frac{{2m{v_0}}}{{m + M}} \Rightarrow A = \frac{V}{\omega },\omega = \sqrt {\frac{k}{M}} \)
+ Nếu đúng lúc vật đến vị trí biên (x=±A0) thì xảy ra va chạm: \(A = \sqrt {x_0^2 + \frac{{{V^2}}}{{{\omega ^2}}}} \)
3. Sau va chạm đàn hồi hai vật tách rời ở vị trí cân bằng
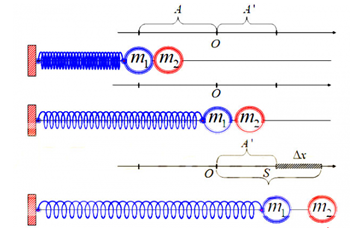
- Giai đoạn 1: Cả hai vật cùng dao động với biên độ A, tần số góc \(\omega = \sqrt {\frac{k}{{{m_1} + {m_2}}}} \) và tốc độ cực đại v0=ωA
- Giai đoạn 2: Nếu đến VTCB m2 tách ra khỏi m1 thì m1 dao động điều hòa với tần số góc và biên độ:
\(\omega = \sqrt {\frac{k}{{{m_1}}}} ,A' = \frac{{{v_0}}}{\omega } = A\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \)
(Vì tốc độ cực đại không đổi vẫn là vo)
m2 chuyển động thẳng đều với vận tốc v0 và khi đến vị trí biên dương (lần 1) thì m2 đi được quãng đường: \(S = {v_0}\frac{{T'}}{4} = \frac{1}{2}\pi A\sqrt {\frac{{{m_1}}}{{{m_1} + {m_2}}}} \)
Lúc này khoảng cách giữa hai vật: \(\Delta x = S - A'\)

