PHƯƠNG PHÁP GIẢI BÀI TẬP GIAO THOA ÁNH SÁNG
I. Tính chất vân tại điểm, số vân trên màn
1 - KIẾN THỨC CẦN NHỚ.
Khoảng vân i: \(i = \dfrac{{\lambda D}}{a}\)
=> \(x_s = k.i\); \(x_t = (k + \dfrac{1}{2})i\)
Trong đó:
- λ là bước sóng ánh sáng (m)
- D là khoảng cách từ mặt phẳng S1S2 đến màn M
- a là khoảng cách giữa hai khe S1S2
2 - CÁC DẠNG - PHƯƠNG PHÁP GIẢI
Dạng 1: Xác định tính chất vân tại điểm M biết trước tọa độ xM
Phương pháp:
Bước 1: Lập tỉ số \(\dfrac{{{x_M}}}{i} = a\)
Bước 2: Xét:
- Nếu \(a = k \in Z\) thì M là vân sáng bậc k
- Nếu \(a = k + 0,5(k \in Z)\) thì M là vân tối
Dạng 2: Xác định số vân sáng, tối trên màn
- TH 1: Màn đối xứng hay M, N đối xứng nhau qua vân sáng trung tâm (MN = L )
- Cách giải đại số:
\( - \dfrac{L}{2} \le {x_M} \le \dfrac{L}{2} \leftrightarrow \left\langle \begin{array}{l} - \dfrac{L}{2} \le ki \le \dfrac{L}{2} \to \left\{ \begin{array}{l} - \dfrac{L}{{2i}} \le k \le \dfrac{L}{{2i}}\\k \in Z\end{array} \right.{\rm{ (1)}}\\ - \dfrac{L}{2} \le (k + 0,5)i \le \dfrac{L}{2} \to \left\{ \begin{array}{l} - \dfrac{1}{2} - \dfrac{L}{{2i}} \le k \le - \dfrac{1}{2} + \dfrac{L}{{2i}}\\k \in Z\end{array} \right.{\rm{ (2)}}\end{array} \right.\)
(1): xác định số vân sáng
(2): xác định số vân tối
- Cách giải nhanh:
- Số vân sáng: \({N_S} = 2\left[ {\dfrac{L}{{2i}}} \right] + 1\) , trong đó: \(\left[ {\dfrac{L}{{2i}}} \right]\) là phần nguyên của \(\dfrac{L}{{2i}}\)
Ví dụ: \(\left[ {\dfrac{L}{{2i}}} \right] = \left[ {3,7} \right] = 3\)
- Số vân tối:
Nếu phần thập phân của \(\dfrac{L}{{2i}} < 0,5\)thì Nt = NS - 1
Nếu phần thập phân của \(\dfrac{L}{{2i}} \ge 0,5\)thì Nt = NS + 1
- TH 2: M, N không đối xứng nhau qua vân sáng trung tâm (M, N khác phía so với vân sáng trung tâm)
- Cách giải đại số:
\( - ON \le {x_M} \le OM \leftrightarrow \left\langle \begin{array}{l} - ON \le ki \le OM \to \left\{ \begin{array}{l} - \dfrac{{ON}}{i} \le k \le \frac{{OM}}{i}\\k \in Z\end{array} \right.{\rm{ (1)}}\\ - ON \le (k + 0,5) \le OM \to \left\{ \begin{array}{l} - \dfrac{1}{2} - \dfrac{{ON}}{i} \le k \le - \dfrac{1}{2} + \dfrac{{OM}}{i}\\k \in Z\end{array} \right.{\rm{ (2)}}\end{array} \right.\)
(1): xác định số vân sáng
(2): xác định số vân tối
- Cách giải nhanh:
\({N_S} = \left[ {\dfrac{{ON}}{i}} \right] + \left[ {\dfrac{{OM}}{i}} \right] + 1\)
\({N_t} = \left[ {\dfrac{{ON}}{i} + 0,5} \right] + \left[ {\dfrac{{OM}}{i} + 0,5} \right]\)
- TH 3: M, N cùng phía so với vân sáng trung tâm
- Cách giải đại số:
\(ON \le {x_M} \le OM \leftrightarrow \left\langle \begin{array}{l}ON \le ki \le OM \to \left\{ \begin{array}{l}\dfrac{{ON}}{i} \le k \le \dfrac{{OM}}{i}\\k \in Z\end{array} \right.{\rm{ (1)}}\\ON \le (k + 0,5) \le OM \to \left\{ \begin{array}{l} - \dfrac{1}{2} + \dfrac{{ON}}{i} \le k \le - \dfrac{1}{2} + \dfrac{{OM}}{i}\\k \in Z\end{array} \right.{\rm{ (2)}}\end{array} \right.\)
(1): xác định số vân sáng
(2): xác định số vân tối
- Cách giải nhanh:
\({N_S} = \left[ {\dfrac{{OM}}{i}} \right] - \left[ {\dfrac{{ON}}{i}} \right]\)
\({N_t} = \left[ {\dfrac{{OM}}{i} + 0,5} \right] - \left[ {\dfrac{{ON}}{i} + 0,5} \right]\)
II. Dịch nguồn - Đặt bản mỏng
1. DỊCH CHUYỂN NGUỒN SÁNG S
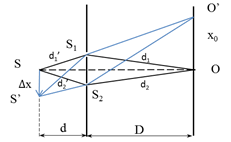
Quang trình: đường đi của ánh sáng.
\(\left\{ \begin{array}{l}{S_1}:{d_1}' + {d_1}\\{S_2}:{d_2}' + {d_2}\end{array} \right. \to \) Tại vị trí vân trung tâm: \({d_1}' + {\rm{ }}{d_1} = {\rm{ }}{d_2}{\rm{' }} + {\rm{ }}{d_2} \to \left( {{d_1}{\rm{' }} + {\rm{ }}{d_1}} \right) - \left( {{d_2}{\rm{' }} + {\rm{ }}{d_2}} \right){\rm{ }} = {\rm{ }}0 = 0\frac{{\lambda D}}{a}\)
=> Tại O là vân trung tâm
Dịch nguồn S một khoảng \(\Delta x \to {d_1}';{d_1}\) thay dổi => Vị trí vân trung tâm thay đổi
\(\begin{array}{l}{d_1}{\rm{' }} + {\rm{ }}{d_1} = {\rm{ }}{d_2}{\rm{' }} + {\rm{ }}{d_2} \to \left| {{d_1}' - {d_2}'} \right| = \left| {{d_1} - {d_2}} \right|\\ \leftrightarrow \frac{{a\Delta x}}{d} = \frac{{{\rm{a}}{{\rm{x}}_0}}}{D} \to {x_0} = \frac{{\Delta xD}}{d}\end{array}\)
2. ĐẶT TRƯỚC S1 (HOẶC S2) MỘT LƯỠNG CHẤT PHẲNG CÓ BỀ DÀY e VÀ CHIẾT SUẤT n
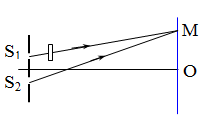
- Ta có:
- Vận tốc ánh sáng trong lưỡng chất phẳng: \(v = \frac{c}{n}\)
- Thời gian ánh sáng đi trong lưỡng chất phẳng: \(\Delta t = \frac{e}{v} = \frac{{en}}{c}\)
- Cũng trong thời gian ∆t đó thì ánh sáng đi ở môi trường ngoài 1 đoạn khác: \(\Delta x = c\Delta t = en\)
- Quang lộ: \({S_1}M = {d_1} + (n - 1)e\), \({S_2}M = {d_2} = {d_1}\)
=> Hiệu quang trình: \(\delta = {S_2}M - {S_1}M = {d_2}-{d_1}-\left( {n-1} \right)e\)
Mà: \({d_2}-{d_1} = \frac{{ax}}{D} \to \delta = \frac{{ax}}{D}-\left( {n-1} \right)e\)
Vân sáng trung tâm ứng với hiệu quang trình bằng \(\delta \)= 0.
\(\delta = \frac{{{\rm{ }}a{x_0}}}{D}-\left( {n-1} \right)e = 0\)
Hay: \({x_0} = \frac{{(n - 1)eD}}{a}\).
Hệ thống vân dịch chuyển về phía S1. Vì \({x_0} > 0\) .
III. Giao thoa 2 ánh sáng - 3 ánh sáng
1. MÀU SẮC VÀ BƯỚC SÓNG ÁNH SÁNG

2. GIAO THOA 2 ÁNH SÁNG \(({\lambda _{\bf{1}}},{\lambda _{\bf{2}}})\)
Ta có: \({i_1} = \dfrac{{{\lambda _1}D}}{a},{\rm{ }}{i_2} = \dfrac{{{\lambda _2}D}}{a}\)
- Khi 2 vân sáng của hai bức xạ trùng nhau (vân sáng cùng màu với vân sáng trung tâm) thì: \({x_{{S_1}}} = {x_{{S_2}}} \to {k_1}\dfrac{{{\lambda _1}D}}{a} = {k_2}\dfrac{{{\lambda _2}D}}{a} \to {k_1}{\lambda _1} = {k_2}{\lambda _2}\)
\( \to \dfrac{{{k_1}}}{{{k_2}}} = \dfrac{{{\lambda _2}}}{{{\lambda _1}}}\) (Phân số tối giản)
- Khoảng cách giữa hai vân sáng cùng màu với vân sáng trung tâm là: \(\Delta x = \dfrac{{{k_1}{\lambda _1}D}}{a} = \dfrac{{{k_2}{\lambda _2}D}}{a} = {i_ \equiv }\)
- Số vân sáng:
+ Của bức xạ 1: \({N_{{S_1}}} = 2\left[ {\dfrac{L}{{2{i_1}}}} \right] + 1\)
+ Của bức xạ 2: \({N_{{S_2}}} = 2\left[ {\dfrac{L}{{2{i_2}}}} \right] + 1\)
+ trùng nhau của 2 bức xạ: \({\rm{ }}{{\rm{N}}_ \equiv } = 2\left[ {\dfrac{L}{{2{i_ \equiv }}}} \right] + 1\)
Số vân sáng quan sát được trên màn: \({N_S} = {\rm{ }}{N_{S1}} + {\rm{ }}{N_{S2}} - {\rm{ }}{N_ \equiv }\)
- Vị trí vân tối trùng nhau:
\(\begin{array}{l}{x_{{T_1}}} = \left( {{k_1} + \dfrac{1}{2}} \right)\dfrac{{{\lambda _1}D}}{a},{\rm{ }}{x_{{T_2}}} = \left( {{k_2} + \dfrac{1}{2}} \right)\dfrac{{{\lambda _2}D}}{a}\\{x_{{T_1}}} = {x_{{T_2}}} \to \left( {{k_1} + \dfrac{1}{2}} \right){\lambda _1} = \left( {{k_2} + \dfrac{1}{2}} \right){\lambda _2}\end{array}\)
3. GIAO THOA 3 ÁNH SÁNG \(({\lambda _{\bf{1}}},{\lambda _{\bf{2}}},{\lambda _{\bf{3}}})\)
Vị trí vân sáng trùng nhau của 3 bức xạ:
\( \to {x_1} = {x_2} = {x_3} \leftrightarrow {k_1}{\lambda _1} = {\rm{ }}{k_2}{\lambda _2} = {\rm{ }}{k_3}{\lambda _3}\)
Giao thoa ánh sáng trắng
Nguồn S là ánh sáng trắng có bước sóng: (0,4μm-0,76μm)
- Trên màn quan sát sẽ thu được: Vân sáng trung tâm có màu trắng (chồng chập của tất cả các màu), lân cận sẽ là các dải màu từ tím đế đỏ, có các vân tối xen kẽ.
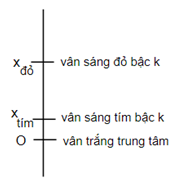
- Cho vị trí x bất kì:
- Xét tại x có số vân sáng trùng nhau:
\(\left\{ \begin{array}{l}x = k\frac{{\lambda D}}{a}\\{\lambda _{\min }} \le \lambda \le {\lambda _{{\rm{max}}}}\end{array} \right. \to \frac{{{\rm{ax}}}}{{{\lambda _{{\rm{max}}}}D}} \le k \le \frac{{{\rm{ax}}}}{{{\lambda _{\min }}D}}\)
- Xét tại x có số vân tối trùng nhau:
\(\left\{ \begin{array}{l}x = (k + \frac{1}{2})\frac{{\lambda D}}{a}\\{\lambda _{\min }} \le \lambda \le {\lambda _{{\rm{max}}}}\end{array} \right. \to \frac{{{\rm{ax}}}}{{{\lambda _{{\rm{max}}}}D}} \le k + \frac{1}{2} \le \frac{{{\rm{ax}}}}{{{\lambda _{\min }}D}}\)
- Bề rộng quang phổ bậc k:
\(\Delta x = {x_{{d_k}}} - {x_{{t_k}}} = k\frac{{{\lambda _d}D}}{a} - k\frac{{{\lambda _t}D}}{a} = ({\lambda _d} - {\lambda _t})k\frac{D}{a}\)
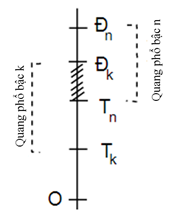
- Sự chồng chập quang phổ:
Đoạn chồng chập quang phổ bậc n với quang phổ bậc k (k<n)
\(\Delta x = {x_{{d_k}}} - {x_{{t_n}}} = k\frac{{{\lambda _d}D}}{a} - n\frac{{{\lambda _t}D}}{a} = (k{\lambda _d} - n{\lambda _t})\frac{D}{a}\)

