Đề bài
Một vật chuyển động điều hòa phải mất 0,25 s để đi từ điểm có vận tốc bằng 0 tới điểm tiếp theo cũng có vận tốc bằng 0. Khoảng cách giữa hai điểm là 36 cm. Tính:
a) Chu kì. b) Tần số. c) Biên độ.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Sử dụng hệ thức độc lập với thời gian của x và v: \({{{x^2}} \over {{A^2}}} + {{{v^2}} \over {{\omega ^2}{A^2}}} = 1\)
Lời giải chi tiết
Ta có:
\(\eqalign{
& {{{x^2}} \over {{A^2}}} + {{{v^2}} \over {{\omega ^2}{A^2}}} = 1 \Rightarrow v = \pm \omega \sqrt {{A^2} - {x^2}} \cr
& = > v = 0 \Leftrightarrow \omega \sqrt {{A^2} - {x^2}} = 0 = > x = A \cr} \)
=> vận tốc bằng 0 khi vật đi qua vị trí biên
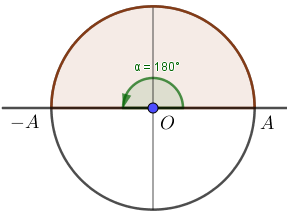
Góc mà vật quét được khi đi từ biên này sang biên kia là \(\Delta \varphi =180^0=\pi=\omega \Delta t\)
=> Khoảng thời gian giữa hai lần liên tiếp vận tốc bằng 0 (vật đi từ biên này đến biên kia) là \(\Delta t=\dfrac{\Delta \varphi}{\omega}=\dfrac{\pi}{\dfrac{2\pi}{T}}= \dfrac{T }{2} = 0,25s\) và khoảng cách giữa hai biên bằng \(2A = 36cm\)
a)
Ta suy ra chu kì dao động của vật: \(T = 2.0,25=0,5s\)
b) Tần số dao động của vật: \(f=\dfrac{1 }{T}=\dfrac{1}{0,5}=2Hz\)
c) Biên độ dao động của vật: \(A =\dfrac{36}{2}= 18cm\)