Đề bài
Hãy tìm lại hai công thức (5.1 SGK) và (5.2 SGK).
Video hướng dẫn giải
Lời giải chi tiết
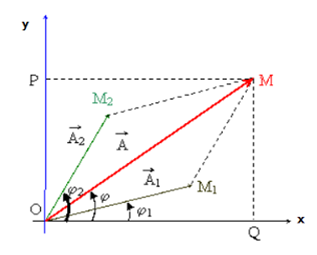
Ta có định lý hàm cos:
\(\eqalign{& {A^2} = A{}_1^2 + A{}_2^2 - 2{A_1}{A_2}\cos \left[ {\pi - \left( {{\varphi _2} - {\varphi _1}} \right)} \right] \cr & {A^2} = A{}_1^2 + A{}_2^2 + 2{A_1}{A_2}\cos \left( {{\varphi _2} - {\varphi _1}} \right) \cr} \)
Theo hình vẽ: \(\overrightarrow A = \overrightarrow {{A_1}} + \overrightarrow {{A_2}} \,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Chiếu (1) trục Ox:
\(A\cos \varphi = {A_1}\cos {\varphi _1} + {A_2}\cos {\varphi _2}\,\,\,\,\,\,\,\,\left( 2 \right)\)
Chiếu (1) trục Oy:
\(A\sin \varphi = {A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}\,\,\,\,\,\,\,\,\left( 3 \right)\)
Lập tỉ số:
\({{\left( 3 \right)} \over {\left( 2 \right)}} \Rightarrow \tan \varphi = {{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}} \over {{A_1}\cos {\varphi _1} + {A_2}\cos {\varphi _2}}}\)

