Đề bài
A. PHẦN TRẮC NGHIỆM (gồm 25 câu – 8 điểm)
Câu 1: Cường độ dòng điện trong mạch không phân nhánh có dạng \(i = 2\sqrt 2 \cos 100\pi t\left( A \right)\). Cường độ dòng điện hiệu dụng trong mạch là
A. I = 2,83 (A) B. I = 2 (A)
C. I = 1,41 (A) D. I = 4 (A)
Câu 2: Đặt vào giữa hai đầu một đoạn mạch điện chỉ có điện trở thuần \(R = 220\Omega \) một điện áp xoay chiều có biểu thức \(u = 220\sqrt 2 \cos \left( {100\pi t - \frac{\pi }{3}} \right)V\). Biểu thức cường độ dòng điện chạy qua điện trở thuần R là
A. \(i = 2\cos \left( {100\pi t - \frac{\pi }{3}} \right)\left( A \right)\)
B. \(i = 2\cos \left( {100\pi t + \frac{\pi }{3}} \right)\left( A \right)\)
C. \(i = \sqrt 2 \cos \left( {100\pi t - \frac{\pi }{3}} \right)\left( A \right)\)
D. \(i = \sqrt 2 \cos \left( {100\pi t - \frac{\pi }{6}} \right)\left( A \right)\)
Câu 3: Đại lượng nào sau đây được gọi là hệ số công suất của mạch điện xoay chiều?
A. \(k = \tan \varphi \) B. \(k = \sin \varphi \)
C. \(k = \cos \varphi \) D. \(k = \cot \varphi \)
Câu 4: Một vật dao động điều hòa theo phương trình \(x = 20\cos \left( {2\pi t + \frac{\pi }{6}} \right)\left( {cm} \right)\) thì gốc thời gian chọn lúc
A. vật có li độ x = -10 cm theo chiều dương
B. vật có li độ \(x = 10\sqrt 3 cm\) theo chiều âm
C. vật có li độ x = 10 cm theo chiều âm
D. vật có li độ \(x = 10\sqrt 3 cm\) theo chiều dương
Câu 5: Nhận xét nào sau đây về máy biến áp là không đúng?
A. Máy biến áp có thể tăng điện áp
B. Máy biến áp có tác dụng biến đổi cường độ dòng điện
C. Máy biến áp có thể thay đổi tần số dòng điện xoay chiều
D. Máy biến áp có thể giảm điện áp
Câu 6: Theo định nghĩa dòng điện xoay chiều hình sin là
A. dòng điện có cường độ biến thiên tỉ lệ thuận với thời gian
B. dòng điện có cường độ biến thiên điều hòa theo thời gian
C. dòng điện có cường độ biến thiên tuần hoàn theo thời gian
D. dòng điện có cường độ biến thiên tỉ lệ nghịch với thời gian
Câu 7: Điều kiện giao thoa hai sóng
A. Hai sóng cùng bước sóng, biên độ
B. Hai sóng cùng phương, cùng tần số, hiệu số pha không đổi theo thời gian
C. Hai sóng bất kì
D. Hai sóng cùng chu kì và biên độ
Câu 8: Công thức tính cảm kháng của cuộn cảm L với dòng điện xoay chiều có tần số f là
A. \({Z_L} = \pi fL\) B. \({Z_L} = \frac{1}{{2\pi fL}}\)
C. \({Z_L} = \frac{1}{{\pi fL}}\) D. \({Z_L} = 2\pi fL\)
Câu 9: Đặt vào hai đầu một đoạn mạch điện xoay chiều một điện áp \(u = 100\cos \left( {100\pi t} \right)V\), cường độ dòng điện qua mạch là \(i = 2\cos \left( {100\pi t + \frac{\pi }{3}} \right)A\). Công suất tiêu thụ trong đoạn mạch này là
A. P = 400 W B. P = 200 W
C. P = 100 W D. P = 50 W
Câu 10: Tại một nơi, chu kỳ dao động điều hòa của amột con lắc đơn là T = 2s. Sau khi tăng chiều dài của con lắc thêm 21 cm thì chu kì dao động điều hòa của nó là 2,2 (s). Chiều dài ban đầu của con lắc là
A. \(l = 90cm\) B. \(l = 121cm\)
C. \(l = 100cm\) D. \(l = 110cm\)
Câu 11: Một vật tham gia đồng thời hai dao động điều hòa cùng phương, có phương trình lần lượt là \({x_1} = 3\cos \left( {20t + \frac{\pi }{3}} \right)cm\) và \({x_2} = 4\cos \left( {20t - \frac{\pi }{6}} \right)cm\). Biên độ dao động tổng hợp của vật là
A. 1 cm B. 7 cm
C. 5 cm D. 5 mm
Câu 12: Một vật dao động điều hòa theo phương trình \(x = 6\cos \left( {4\pi t} \right)cm\). Biên độ dao động của vật là
A. 6 cm B. 36 cm
C. 12 m D. \(4\pi \left( {cm} \right)\)
Câu 13: Một con lắc lò xo có độ cứng k = 50N/m dao động điều hòa với chiều dài quỹ đạo là 20 cm. Cơ năng dao động của con lắc lò xo là
A. 0,025 J B. 1 J
C. 10kJ D. 0,25 J
Câu 14: Một lá thép mỏng, một đầu cố định, đầu còn lại được kích thích để dao động với chu kì không đổi và bằng 0,10 s. Sóng âm do lá thép phát ra là
A. hạ âm B. âm nghe được
C. nhạc âm D. siêu âm
Câu 15: Cho mạch R, L, C mắc nối tiếp có \(R = 20\sqrt 3 \Omega ,L = \frac{{0,6}}{\pi }\left( H \right),C = \frac{{{{10}^{ - 3}}}}{{4\pi }}\left( F \right)\). Đặt vào hai đầu mạch điện một điện áp \(u = 200\sqrt 2 \cos \left( {100\pi t} \right)V\). Biểu thức cường độ dòng điện trong mạch là
A. \(i = 5\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{6}} \right)\left( A \right)\)
B. \(i = 5\sqrt 2 \cos \left( {100\pi t - \frac{\pi }{3}} \right)\left( A \right)\)
C. \(i = 5\sqrt 2 \cos \left( {100\pi t + \frac{\pi }{3}} \right)\left( A \right)\)
D. \(i = 5\sqrt 2 \cos \left( {100\pi t - \frac{\pi }{6}} \right)\left( A \right)\)
Câu 16: Khi có sóng dừng trên dây, khoảng cách giữa hai nút liên tiêp bằng
A. một phần tư bước sóng
B. một số nguyên lần bước sóng
C. một bước sóng
D. một nửa bước sóng
Câu 17: Trong thí nghiệm giao thoa sóng nước hai nguồn kết hợp S1S2 cách nhau 11 cm, có chu kì sóng là T = 0,2 (s). Tốc độ truyền sóng trong môi trường là v = 25 cm/s. Số điểm cực đại giao thoa trong khoảng S1S2 là:
A. 6 B. 4
C. 5 D. 9
Câu 18: Mạch điện xoay chiều gồm RLC mắc nối tiếp, có \(R = 30\Omega ,{Z_C} = 20\Omega ,{Z_L} = 60\Omega \). Tổng trở của mạch là
A. \(Z = 50\Omega \) B. \(Z = 2500\Omega \)
C. \(Z = 10\Omega \) D. \(Z = 70\Omega \)
Câu 19: Để phân loại sóng ngang và sóng dọc người ta dựa vào
A. phương dao động và phương truyền sóng
B. tốc độ truyền sóng và bước sóng
C. phương dao động và tốc độ truyền sóng
D. phương truyền sóng và tần số sóng
Câu 20: Một con lắc đơn chiều dài l dao động điều hòa tại nơi có gia tốc trọng trường với biên độ góc nhỏ hơn 100. Chu kì dao động của nó là:
A. \(T = \frac{1}{{2\pi }}\sqrt {\frac{l}{g}} \)
B. \(T = 2\pi \sqrt {\frac{l}{g}} \)
C. \(T = 2\pi \sqrt {\frac{g}{l}} \)
D. \(T = \sqrt {\frac{g}{l}} \)
Câu 21: Cơ năng của một con lắc lò xo tỉ lệ thuận với:
A. bình phương biên độ dao động
B. li độ dao động
C. biên độ dao động
D. tần số dao động
Câu 22: Mắc tụ điện như hình dưới vào mạng điện xoay chiều tần số 60 Hz thì dung kháng của tụ có giá trị gần nhất với giá trị nào sau đây:
A. \(100\Omega \) B. \(120\Omega \)
C. \(2653\Omega \) D. \(3184\Omega \)
Câu 23: Một máy biến áp lý tưởng có số vòng dây của cuộn sơ cấp là 500 vòng, của cuộn thứ cấp là 50 vòng. Điện áp và cường độ dòng điện hiệu dụng ở mạch thứ cấp là 100 V và 10 A. Điện áp và cường độ dòng điện hiệu dụng ở mạch sơ cấp là
A. 1000 (V); 100 (A) B. 1000 (V); 1 (A)
C. 10 (V); 100 (A) D. 10 (V); 1 (A)
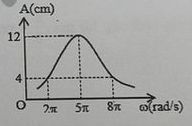
Câu 24: Một con lắc lò co có khối lượng 100g dao động cưỡng bức ổn định dưới tác dụng của ngoại lực biến thiên điều hòa với tần số f. Đồ thị biểu diễn sự phụ thuộc của biên độ vào tần số của ngoại lực tác dụng lên hệ có dạng như hình vẽ. Lấy \({\pi ^2} = 10\). Độ cứng của lò xo là
A. 25 N/m B. 42,25 N/m
C. 75 N/m D. 100 N/m
Câu 25: Một sợi dây căng giữa hai điểm cố định cách nhau 80 cm. Hai sóng có tần số gần nhau liên tiếp cùng tạo ra sóng dừng trên dây là \({f_1} = 70Hz\) và \({f_2} = 84Hz\). Tìm tốc độ truyền sóng trên dây. Biết tốc độ truyền sóng trên dây không đổi.
A. 11,2 m/s B. 22,4 m/s
C. 26,9 m/s D. 18,7 m/s
B. TỰ LUẬN (2 đ)
Câu 1 (0,5đ): Một vật dao động điều hòa có biên độ A = 5 cm, tần số 10 Hz, chọn gốc thời gian sao cho pha ban đầu bằng 0, viết phương trình dao động của vật.
Câu 2 (0,5đ): Sóng truyền dọc theo trục Ox có bước sóng 40 cm và tần số 8 Hz. Tính chu kì và tốc độ truyền sóng.
Câu 3 (1,0đ): Cho mạch RLC nối tiếp gồm: \(R = 40\Omega ,L = \frac{{0,8}}{\pi }\left( H \right),C = \frac{1}{{4000\pi }}\left( F \right)\). Điện áp giữa hai đầu đoạn mạch có biểu thức \(u = 120\sqrt 2 \cos 100\pi t\left( V \right)\).
a) Tính tổng trở của mạch
b) Viết biểu thức cường độ dòng điện chạy trong mạch và biểu thức điện áp \({u_{AM}}\) giữa hai đầu đoạn mạch R,C.
Lời giải chi tiết
HƯỚNG DẪN GIẢI CHI TIẾT
Thực hiện: Ban chuyên môn
A. PHẦN TRẮC NGHIỆM
| 1. B | 2. C | 3. C | 4. B | 5. C |
| 6. B | 7. B | 8. D | 9. D | 10. C |
| 11. C | 12. A | 13. D | 14. A | 15. D |
| 16. D | 17. C | 18. A | 19. A | 20. B |
| 21. A | 22. C | 23. B | 24. A | 25. B |
Câu 1:
Phương pháp
Cường độ dòng điện hiệu dụng: \(I = \frac{{{I_0}}}{{\sqrt 2 }}\)
Cách giải
Cường độ dòng điện hiệu dụng: \(I = \frac{{{I_0}}}{{\sqrt 2 }} = \frac{{2\sqrt 2 }}{{\sqrt 2 }} = 2\left( A \right)\)
Chọn B
Câu 2:
Phương pháp
Đoạn mạch chỉ có điện trở thuần R: u, i cùng pha.
Cường độ dòng điện: \(I = \frac{U}{R}\)
Cách giải
Đoạn mạch chỉ có điện trở thuần R: u, i cùng pha => \({\varphi _i} = {\varphi _u} = - \frac{\pi }{3}\)
Cường độ dòng điện cực đại qua R là:
\({I_0} = \frac{{{U_0}}}{R} = \frac{{220\sqrt 2 }}{{220}} = \sqrt 2 \left( A \right)\)
Vậy \(i = \sqrt 2 \cos \left( {100\pi t - \frac{\pi }{3}} \right)\left( A \right)\)
Chọn C
Câu 3:
Phương pháp
Vận dụng lý thuyết hệ số công suất của mạch điện xoay chiều.
Cách giải
Hệ số công suất của mạch điện xoay chiều là \(k = \cos \varphi \).
Chọn C
Câu 4:
Phương pháp
Phương trình li độ: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Phương trình vận tốc: \(v = - \omega A\sin \left( {\omega t + \varphi } \right)\)
Cách giải
Thay t = 0 vào phương trình ta được:
\(x = 20\cos \frac{\pi }{6} = 10\sqrt 3 \left( {cm} \right)\)
\(v = - 2\pi .20\sin \frac{\pi }{6} = - 20\pi \left( {m/s} \right)\) < 0
=> Gốc thời gian là lúc vật có li độ \(x = 10\sqrt 3 cm\) theo chiều âm.
Chọn B
Câu 5:
Phương pháp
Vận dụng lý thuyết về máy biến áp.
Cách giải
Máy biến áp không làm thay đổi tần số dòng điện xoay chiều.
Chọn C
Câu 6:
Phương pháp
Vận dụng lý thuyết về dòng điện xoay chiều.
Cách giải
Dòng điện xoay chiều hình sin là dòng điện có cường độ biến đổi điều hòa theo thời gian.
Chọn B
Câu 7:
Phương pháp
Điều kiện giao thoa hai sóng là: hai sóng cùng phương, cùng tần số và có hiệu số pha không đổi theo thời gian
Cách giải
Điều kiện giao thoa hai sóng là: hai sóng cùng phương, cùng tần số và có hiệu số pha không đổi theo thời gian.
Chọn B
Câu 8:
Phương pháp
Cảm kháng \({Z_L} = \omega L\)
Cách giải
Cảm kháng \({Z_L} = \omega L = 2\pi fL\)
Chọn D
Câu 9:
Phương pháp
Độ lệch pha giữa u và i là: \(\varphi = {\varphi _u} - {\varphi _i}\)
Công suất tiêu thụ: \(P = U.I.\cos \varphi \)
Cách giải
Độ lệch pha giữa u và i là:
\(\varphi = {\varphi _u} - {\varphi _i} = 0 - \frac{\pi }{3} = - \frac{\pi }{3}\)
Hệ số công suất: \(k = \cos \varphi = \cos \left( { - \frac{\pi }{3}} \right) = 0,5\)
Công suất tiêu thụ trong đoạn mạch là:
\(P = U.I.\cos \varphi = \frac{{100}}{{\sqrt 2 }}.\frac{2}{{\sqrt 2 }}.0,5 = 50{\rm{W}}\)
Chọn D
Câu 10:
Phương pháp
Chu kì dao động của con lắc đơn là:
\(T = 2\pi \sqrt {\frac{l}{g}} \)
Cách giải
Ta có:
\({T_1} = 2\pi \sqrt {\frac{{{l_1}}}{g}} \)
\({T_2} = 2\pi \sqrt {\frac{{{l_1} + 0,21}}{g}} \)
Suy ra: \(\frac{{T_1^2}}{{T_2^2}} = \frac{{{l_1}}}{{{l_1} + 0,21}} \Leftrightarrow \frac{{{2^2}}}{{2,{2^2}}} = \frac{{{l_1}}}{{{l_1} + 0,21}}\)
\( \Rightarrow {l_1} = 1m = 100cm\)
Chọn C
Câu 11:
Phương pháp
Biên độ của dao động tổng hợp là:
\({A^2} = A_1^2 + A_2^2 + 2{{\rm{A}}_1}{A_2}\cos \left( {{\varphi _2} - {\varphi _1}} \right)\)
Cách giải
Biên độ của dao động tổng hợp là:
\({A^2} = A_1^2 + A_2^2 + 2{{\rm{A}}_1}{A_2}\cos \left( {{\varphi _2} - {\varphi _1}} \right)\)
\( \Leftrightarrow A = \sqrt {{3^2} + {4^2} + 2.3.4.\cos \left( { - \frac{\pi }{6} - \frac{\pi }{3}} \right)} \)
\( \Leftrightarrow A = 5cm\)
Chọn C
Câu 12:
Phương pháp
Phương trình li độ: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Cách giải
Phương trình li độ: \(x = A\cos \left( {\omega t + \varphi } \right)\)
Suy ra biên độ A = 6 cm
Chọn A
Câu 13:
Phương pháp
Chiều dài quỹ đạo l = 2A.
Cơ năng của con lắc lò xo: \({\rm{W}} = \frac{1}{2}k{A^2}\)
Cách giải
Biên độ dao động của con lắc là:
\(A = \frac{l}{2} = \frac{{20}}{2} = 10cm\)
Cơ năng của con lắc lò xo:
\({\rm{W}} = \frac{1}{2}k{A^2} = \frac{1}{2}.50.0,{1^2} = 0,25J\)
Chọn D
Câu 14:
Phương pháp
Sử dụng công thức tính tần số âm: \(f = \frac{1}{T}\)
Dựa vào lý thuyết về sóng âm để xác định loại âm.
Cách giải
Ta có: Tần số âm: \(f = \frac{1}{T} = \frac{1}{{0,1}} = 10Hz\) < 16 Hz => hạ âm
Chọn A
Câu 15:
Phương pháp
Sử dụng các công thức tính: cảm kháng, dung kháng, tổng trở.
Độ lệch pha giữa u và i: \(\varphi = {\varphi _u} - {\varphi _i};\cos \varphi = \frac{R}{Z}\)
\({I_0} = \frac{{{U_0}}}{Z}\)
Cách giải
Dung kháng: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{{{{10}^{ - 3}}}}{{4\pi }}}} = 40\Omega \)
Cảm kháng: \({Z_L} = \omega L = 100\pi .\frac{{0,6}}{\pi } = 60\Omega \)
Tổng trở:
\(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \\ = \sqrt {{{\left( {20\sqrt 3 } \right)}^2} + {{\left( {60 - 40} \right)}^2}} = 40\Omega \)
Độ lệch pha giữa u và i:
\(\cos \varphi = \frac{R}{Z} = \frac{{20\sqrt 3 }}{{40}} = \frac{{\sqrt 3 }}{2} \Rightarrow \varphi = \frac{\pi }{6}\)
\(\varphi = {\varphi _u} - {\varphi _i} \Rightarrow {\varphi _i} = {\varphi _u} - \varphi \\= 0 - \frac{\pi }{6} = - \frac{\pi }{6}\)
Cường độ dòng điện cực đại:
\({I_0} = \frac{{{U_0}}}{Z} = \frac{{200\sqrt 2 }}{{40}} = 5\sqrt 2 A\)
Vậy \(i = 5\sqrt 2 \cos \left( {100\pi t - \frac{\pi }{6}} \right)\left( A \right)\)
Chọn D
Câu 16:
Phương pháp
Vận dụng lý thuyết về sóng dừng.
Cách giải
Khi có sóng dừng trên dây, khoảng cách giữa hai nút liên tiếp bằng một nửa bước sóng.
Chọn D
Câu 17:
Phương pháp
Điều kiện cực đại giao thoa:
\(\frac{{ - {S_1}{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda }\)
Cách giải
Ta có: \(v = \frac{\lambda }{T} \Rightarrow \lambda = v.T = 25.0,2 = 5cm\\ = 0,05m\)
Số điểm cực đại giao thoa trong khoảng S1S2 là:
\(\begin{array}{l}\frac{{ - {S_1}{S_2}}}{\lambda } < k < \frac{{{S_1}{S_2}}}{\lambda }\\ \Leftrightarrow - \frac{{11}}{5} < k < \frac{{11}}{5}\\ \Leftrightarrow - 2,2 < k < 2,2\end{array}\)
\( \Rightarrow k = - 2, - 1,0,1,2\) => có 5 điểm.
Chọn C
Câu 18:
Phương pháp
Tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
Cách giải
Tổng trở:
\(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \\ = \sqrt {{{30}^2} + {{\left( {60 - 20} \right)}^2}} = 50\Omega \)
Chọn A
Câu 19:
Phương pháp
Vận dụng lý thuyết về định nghĩa sóng ngang và sóng dọc.
Cách giải
Ta phân biệt sóng ngang và sóng dọc dựa vào phương dao động và phương truyền sóng.
Chọn A
Câu 20:
Phương pháp
Chu kì dao động của con lắc đơn là:
\(T = 2\pi \sqrt {\frac{l}{g}} \)
Cách giải
Chu kì dao động của con lắc đơn là:
\(T = 2\pi \sqrt {\frac{l}{g}} \)
Chọn B
Câu 21:
Phương pháp
Cơ năng của con lắc lò xo: \({\rm{W}} = \frac{1}{2}k{A^2}\)
Cách giải
Cơ năng của con lắc lò xo: \({\rm{W}} = \frac{1}{2}k{A^2}\)
=> tỉ lệ thuận với bình phương biên độ dao động.
Chọn A
Câu 22:
Phương pháp
Dung kháng: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}}\)
Cách giải
Dung kháng: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{2\pi fC}}\)
Chọn C
Câu 23:
Phương pháp
Sử dụng công thức :
\(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}} = \frac{{{I_2}}}{{{I_1}}}\)
Cách giải
Ta có:
\(\frac{{{U_1}}}{{{U_2}}} = \frac{{{N_1}}}{{{N_2}}} \Leftrightarrow \frac{{{U_1}}}{{100}} = \frac{{500}}{{50}} \Rightarrow {U_1} = 1000V\)
\(\frac{{{N_1}}}{{{N_2}}} = \frac{{{I_2}}}{{{I_1}}} \Leftrightarrow \frac{{500}}{{50}} = \frac{{10}}{{{I_1}}} \Rightarrow {I_1} = 1{\rm{A}}\)
Chọn B
Câu 24:
Phương pháp
Độ cứng của lò xo: \(k = m{\omega ^2}\)
Cách giải
Từ đồ thị ta thấy khi \(\omega = 5\pi \left( {ra{\rm{d}}/s} \right)\) => xảy ra cộng hưởng.
Độ cứng của lò xo là:
\(k = m{\omega ^2} = 0,1.{\left( {5\pi } \right)^2} = 0,1.25.10 = 25N/m\)
Chọn A
Câu 25:
Phương pháp
Điều kiện sóng dừng hai đầu cố định:
\(l = \frac{{k\lambda }}{2} = \frac{{kv}}{2}\)
Hai tần số gần nhau nhất cùng tạo sóng dừng trên dây thì số bó sóng hơn kém nhau là 1: \({k_2} - {k_1} = 1\)
Cách giải
Điều kiện sóng dừng hai đầu cố định:
\(l = \frac{{k\lambda }}{2} = \frac{{kv}}{2} \Rightarrow kv = 1,6f\)
Hai tần số gần nhau nhất cùng tạo sóng dừng trên dây thì số bó sóng hơn kém nhau là 1 nên ta có:
\(\left\{ \begin{array}{l}{k_1}v = 1,6{f_1}\\{k_2}v = 1,6{f_2}\end{array} \right. \\\Rightarrow v = 1,6.\left( {{f_2} - {f_1}} \right) = 1,6.\left( {84 - 70} \right)\\ = 22,4m/s\)
Chọn B
B. PHẦN TỰ LUẬN
Câu 1:
Phương pháp
Tần số góc: \(\omega = 2\pi f\)
Phương trình dao động: \(x = A\cos \left( {\omega t + \varphi } \right)\left( {cm} \right)\)
Cách giải
Tần số góc: \(\omega = 2\pi f = 2\pi .10 = 20\pi \left( {ra{\rm{d}}/s} \right)\)
Phương trình dao động: \(x = 5\cos \left( {20\pi t} \right)\left( {cm} \right)\)
Câu 2:
Phương pháp
Chu kì \(T = \frac{1}{f}\)
Tốc độ truyền sóng: \(v = \frac{\lambda }{T} = \lambda f\)
Cách giải
Chu kì \(T = \frac{1}{f} = \frac{1}{8} = 0,125{\rm{s}}\)
Tốc độ truyền sóng: \(v = \lambda f = 0,4.8 = 3,2m/s\)
Câu 3:
Phương pháp
Cảm kháng: \({Z_L} = \omega L\)
Dung kháng: \({Z_C} = \frac{1}{{\omega C}}\)
Tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \)
Độ lệch pha: \(\varphi = {\varphi _u} - {\varphi _i};\cos \varphi = \frac{R}{Z}\)
Cách giải
a)
Cảm kháng: \({Z_L} = \omega L = 100\pi .\frac{{0,8}}{\pi } = 80\Omega \)
Dung kháng: \({Z_C} = \frac{1}{{\omega C}} = \frac{1}{{100\pi .\frac{1}{{4000\pi }}}} = 40\Omega \)
Tổng trở: \(Z = \sqrt {{R^2} + {{\left( {{Z_L} - {Z_C}} \right)}^2}} \\ = \sqrt {{{40}^2} + {{\left( {80 - 40} \right)}^2}} = 40\sqrt 2 \Omega \)
b)
Độ lệch pha giữa u và i là:
Ta có: \(\cos \varphi = \frac{R}{Z} = \frac{{40}}{{40\sqrt 2 }} = \frac{{\sqrt 2 }}{2}\)
\(\begin{array}{l} \Rightarrow \varphi = \frac{\pi }{4} = {\varphi _u} - {\varphi _i}\\ \Rightarrow {\varphi _i} = 0 - \frac{\pi }{4} = - \frac{\pi }{4}\end{array}\)
Cường độ dòng điện cực đại:
\({I_0} = \frac{{{U_0}}}{Z} = \frac{{120\sqrt 2 }}{{40\sqrt 2 }} = 3{\rm{A}}\)
Suy ra: \(i = 3\cos \left( {100\pi t - \frac{\pi }{4}} \right)\left( A \right)\)
Điện áp cực đại giữa hai đầu AM là:
\({U_{0AM}} = {I_0}.\sqrt {{R^2} + Z_C^2} \\= 3.\sqrt {{{40}^2} + {{40}^2}} = 120\sqrt 2 \left( V \right)\)
\(\tan {\varphi _{RC}} = \frac{{ - {Z_C}}}{R} = - \frac{{40}}{{40}} = - 1\)
\(\begin{array}{l} \Rightarrow {\varphi _{RC}} = - \frac{\pi }{4} = {\varphi _{uRC}} - {\varphi _i}\\ \Rightarrow {\varphi _{uRC}} = - \frac{\pi }{4} - \frac{\pi }{4} = - \frac{\pi }{2}\end{array}\)
Suy ra: \({u_{AM}} = 120\sqrt 2 \cos \left( {100\pi t - \frac{\pi }{2}} \right)\left( V \right)\)