Phương trình chứa dấu giá trị tuyệt đối

Ta có $\left| {2 + 3x} \right| = \left| {4x - 3} \right|$$\Leftrightarrow \left[ \begin{array}{l}2 + 3x = 4x - 3\\2 + 3x = 3 - 4x\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\7x = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = \dfrac{1}{7}\end{array} \right.$

Vậy nghiệm nhỏ nhất của phương trình là $x = \dfrac{1}{7}$ .

TH1: $\left| {3x - 1} \right| = 3x - 1$ khi $3x - 1 \ge 0 \Leftrightarrow 3x \ge 1 \Leftrightarrow x \ge \dfrac{1}{3}$

Phương trình đã cho trở thành $3x - 1 = x + 4$$\Leftrightarrow 2x = 5$$\Leftrightarrow x = \dfrac{5}{2}\left( {TM} \right)$

TH2: $\left| {3x - 1} \right| = 1 - 3x$ khi $3x - 1 < 0$$\Leftrightarrow x < \dfrac{1}{3}$

Phương trình đã cho trở thành $1 - 3x = x + 4$$\Leftrightarrow 4x =  - 3$$\Leftrightarrow x =  - \dfrac{3}{4}\,\left( {TM} \right)$

Vậy $S = \left\{ {\dfrac{{ - 3}}{4};\dfrac{5}{2}} \right\}$

Tổng các nghiệm của phương trình là $- \dfrac{3}{4} + \dfrac{5}{2} = \dfrac{7}{4}$ .

TH1: $\left| {2x} \right| = 2x$ khi $2x \ge 0 \Leftrightarrow x \ge 0$

Phương trình đã cho trở thành $2x = 3 - 3x \Leftrightarrow 5x = 3 \Leftrightarrow x = \dfrac{3}{5}\,\left( {TM} \right)$

TH2: $\left| {2x} \right| =  - 2x$ khi $2x < 0 \Leftrightarrow x < 0$

Phương trình đã cho trở thành $- 2x = 3 - 3x \Leftrightarrow x = 3\,\left( {KTM} \right)$

Vậy nghiệm lớn nhất của phương trình là $x = 3$ .

Ta có $\left| {1 - x} \right| - \left| {2x - 1} \right| = x - 2\,\,\,\,\left( 1 \right)$         

Xét: $\begin{array}{l} + )\;\;1 - x = 0 \Leftrightarrow x = 1\\ + )\;\;2x - 1 = 0 \Leftrightarrow x = \dfrac{1}{2}\end{array}$      

Ta có bảng xét dấu đa thức $1 - x$ và $2x - 1$ dưới đây

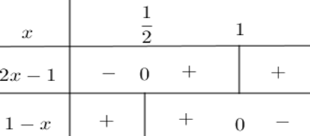
Từ bảng xét dấu ta có:

TH1: $x < \dfrac{1}{2}$ khi đó $\left| {2x - 1} \right| = 1 - 2x;\,\left| {1 - x} \right| = 1 - x$ nên phương trình $\left( 1 \right)$ trở thành

$1 - x - \left( {1 - 2x} \right) = x - 2 \Leftrightarrow 1 - x - 1 + 2x = x - 2 \Leftrightarrow x = x - 2$

$\Leftrightarrow 0 =  - 2$ (vô lý)

TH2: $\dfrac{1}{2} \le x \le 1$, khi đó $\left| {2x - 1} \right| = 2x - 1;\,\left| {1 - x} \right| = 1 - x$ nên phương trình $\left( 1 \right)$ trở thành

$1 - x - \left( {2x - 1} \right) = x - 2 \Leftrightarrow  - 3x + 2 = x - 2 \Leftrightarrow  - 4x =  - 4 \Leftrightarrow x = 1\,\left( {TM} \right)$

TH3: $x > 1$ , khi đó $\left| {2x - 1} \right| = 2x - 1;\,\left| {1 - x} \right| = x - 1$ nên phương trình $\left( 1 \right)$ trở thành

$x - 1 - \left( {2x - 1} \right) = x - 2 \Leftrightarrow  - x = x - 2 \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\,\,\left( {L} \right)$

Vậy phương trình có nghiệm $x = 1$ .

* Xét phương trình $4\left| {2x - 1} \right| + 3 = 15\,\,\,\left( 1 \right)$

TH1: $\left| {2x - 1} \right| = 2x - 1$ khi $x \ge \dfrac{1}{2}$

Phương trình $\left( 1 \right)$ trở thành $4\left( {2x - 1} \right) + 3 = 15$$\Leftrightarrow 4\left( {2x - 1} \right) = 12$$\Leftrightarrow 2x - 1 = 3$$\Leftrightarrow x = 2\,\left( {TM} \right)$

TH2:  $\left| {2x - 1} \right| = 1 - 2x$ khi $x < \dfrac{1}{2}$

Phương trình $\left( 1 \right)$ trở thành $4\left( {1 - 2x} \right) + 3 = 15$$\Leftrightarrow 4\left( {1 - 2x} \right) = 12$$\Leftrightarrow 1 - 2x = 3$$\Leftrightarrow x =  - 1\left( {TM} \right)$

Vậy phương trình $\left( 1 \right)$ có hai nghiệm $x =  - 1;\,x = 2$.

Xét phương trình

$\;\left| {7x + 1} \right| - \left| {5x + 6} \right| = 0\\ \Leftrightarrow \left| {7x + 1} \right| = \left| {5x + 6} \right|\\ \Leftrightarrow \left[ \begin{array}{l}7x + 1 = 5x + 6\\7x + 1 =  - (5x + 6)\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = 5\\12x =  - 7\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{5}{2}\\x =  - \dfrac{7}{{12}}\end{array} \right.$

Vậy phương trình $\left( 2 \right)$ có hai nghiệm là $x = \dfrac{5}{2};x =  - \dfrac{7}{{12}}.$

TH1: $\left| {1 - x} \right| = 1 - x$ với $1 - x \ge 0 \Leftrightarrow x \le 1$

Bất phương trình đã cho trở thành $1 - x \ge 3 \Leftrightarrow x \le  - 2$, kết hợp điều kiện $x \le 1$ ta có $x \le  - 2$.

TH2: $\left| {1 - x} \right| = x - 1$ với $1 - x < 0 \Leftrightarrow x > 1$

Bất phương trình đã cho trở thành $x - 1 \ge 3 \Leftrightarrow x \ge 4$, kết hợp điều kiện $x > 1$ ta có $x \ge 4$.

Vậy bất phương trình có nghiệm $x \ge 4,x \le  - 2$

TH1: $\left| {x - 6} \right| = x - 6$ với $x - 6 \ge 0 \Leftrightarrow x \ge 6$

Bất phương trình đã cho trở thành $x - 6 + 5 \ge x \Leftrightarrow  - 1 \ge 0$ (vô lý)

TH2: $\left| {x - 6} \right| = 6 - x$ với $x - 6 < 0 \Leftrightarrow x < 6$.

Bất phương trình đã cho trở thành $6 - x + 5 \ge x$$\Leftrightarrow  - 2x \ge  - 11$$\Leftrightarrow x \le \dfrac{{11}}{2}$, kết hợp điều kiện $x < 6$ ta có $x \le  \dfrac{{11}}{2}$.

Bất phương trình có tập nghiệm $S = \left\{ x \in R|{x \le \dfrac{{11}}{2}} \right\}$.

Nghiệm nguyên dương lớn nhất thỏa mãn là $x = 5$.

Điều kiện $209x \ge 0 \Leftrightarrow x \ge 0$

$\left| {x + \dfrac{1}{{209}}} \right| + \left| {x + \dfrac{2}{{209}}} \right| + \left| {x + \dfrac{3}{{209}}} \right| + ... + \left| {x + \dfrac{{208}}{{209}}} \right| = 209x\\ \Leftrightarrow x + \dfrac{1}{{209}} + x + \dfrac{2}{{209}} + x + \dfrac{3}{{209}} + ... + x + \dfrac{{100}}{{209}} = 209x\\ \Leftrightarrow 208x + \left( {\dfrac{1}{{209}} + \dfrac{2}{{209}} + \dfrac{3}{{209}} + ... + \dfrac{{208}}{{209}}} \right) = 209x\\ \Leftrightarrow 208x + \dfrac{{104.209}}{{209}} = 209x\\ \Leftrightarrow 208x + 104 = 209x\\ \Leftrightarrow x = 104\;\;(TM)$

Vậy $x = 104.$