Hình thang

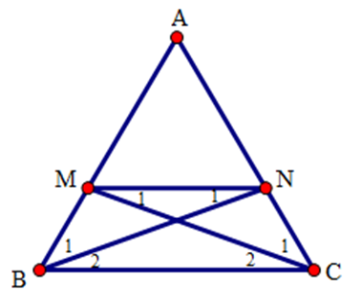
Ta có:$AB = AM + MB$  và  $AC = AN + NC$ . Mà $AB = AC$ (do tam giác $ABC$ cân tại$A$ )và $BM = NC$  ( gt)

Suy ra $AN = AM$

Xét tam giác $AMN$ có: $AM = AN$ (cmt)

Suy ra tam giác $AMN$ cân tại$A$ . Suy ra \(\widehat {AMN} = \widehat {ANM}\)

Xét tam giác $ANM$ có:     \(\widehat A + \widehat {AMN} + \widehat {ANM} = {180^0}\)(tổng ba góc trong một tam giác)

\(\widehat {AMN} = \dfrac{{{{180}^0} - \widehat A}}{2}\)( vì \(\widehat {AMN} = \widehat {ANM}\) )     (1)

 Xét tam giác $ABC$ cân tại $A$ ta có:  \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong một tam giác) nên  $\widehat B = \dfrac{{{{180}^0} - \widehat A}}{2}$  ( vì \(\widehat B = \widehat C\) )       (2)

Từ (1) và (2) \(\widehat {AMN} = \widehat B\)

Mà $\widehat {AMN},\widehat B$là hai góc đồng vị nên $MN$ //$BC$ .

Xét tứ giác $MNCB$ có $MN$ // $BC$ nên $MNCB$ là hình thang.

Lại có \(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại$A$ ) nên $MNCB$ là hình thang cân.

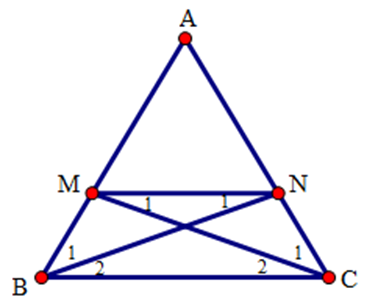
Ta có $BM = MN$ khi và chỉ khi \(\Delta MNB\) cân tại \(M \Rightarrow \)  \(\widehat {{N_1}} = \widehat {{B_1}}\)\( \Leftrightarrow \widehat {{B_1}} = \widehat {{B_2}}\)(vì \(\widehat {{N_1}} = \widehat {{B_2}}\)) nên \(BN\) là phân giác góc $ABC$.

Tương tự $MN = NC$ khi và chỉ khi \(\Delta MNC\) cân tại \(N \Rightarrow \)\(\widehat {{C_1}} = \widehat {{C_2}}\) nên \(CM\) là phân giác góc \(ACB\) .

Như vậy, nếu $BN$ và $CM$ là các đường phân giác của tam giác $ABC$ thì $BM = MN = CN.$

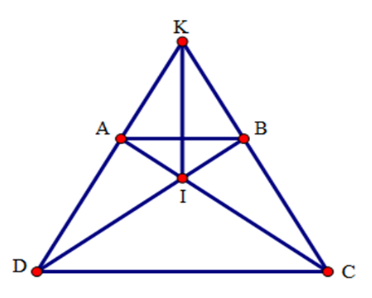
* Xét tam giác $ACD$ và tam giác $BDC$ có:

+$AD = BC$ (do $ABCD$ là hình thang cân)

+ $AC = BD$  (do $ABCD$ là hình thang cân)

  + $CD$ là cạnh chung

 Suy ra \(\Delta ACD = \Delta BDC\)(c.c.c). Suy ra \(\widehat {ACD} = \widehat {BDC}\) (hai góc tương ứng).

Xét tam giác $ICD$ có \(\widehat {ACD} = \widehat {BDC}\)(cmt), suy ra tam giác $ICD$ cân tại$I$ .Dođó $ID = IC\,\,\,\left( 1 \right)$

 Tam giác $KCD$ có hai góc ở đáy bằng nhau nên tam giác $KCD$ cân ở$K$ . Do đó $KC = KD$$\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $KI$ là đường trung trực của$CD$    (*)

* Xét tam giác $ADB$ và tam giác $BCA$ có:

+ $AD = BC$  (cmt)

+ $AB$ là cạnh chung

+ $AC = BD$

Suy ra \(\Delta ADB = \Delta BCA\) (c.c.c). Suy ra \(\widehat {ABD} = \widehat {BAC}\) .

Xét tam giác $IAB$ có \(\widehat {ABD} = \widehat {BAC}\) nên tam giác $IAB$ cân tại$I$ . Do đó $IA = IB$$\left( 3 \right)$

Ta có:$KA = KD-AD$ ;$KB = KC-BC$ . Mà$KD = KC$ , $AD = BC$ , do đó $KA = KB$$\left( 4 \right)$

Từ $\left( 3 \right)$ và $\left( 4 \right)$ suy ra $KI$ là đường trung trực của$AB$ .   (**)

Từ (*) và (**) suy ra $KI$ là đường trung trực của hai đáy (đpcm)

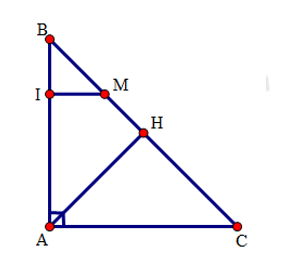
Tứ giác \(ACMI\) có: \(MI//AC\left( {gt} \right)\) và \(\hat A = 90^\circ (gt)\) nên là hình thang vuông.

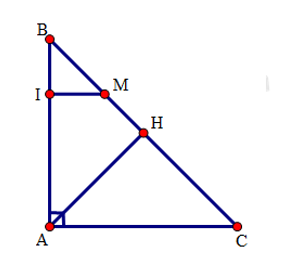
Xét tam giác \(AMC\) có: \(CM = AC(gt)\) nên tam giác \(AMC\) cân tại \(C\).

Suy ra \(\widehat {MAC} = \widehat {AMC\,}\,\,(1)\)

Xét tam giác AMH có: \(\widehat {MAH} = 90^\circ \widehat {- AMH}\) (hai góc phụ nhau) (2)

Xét tam giác ABC vuông tại A: \(\widehat {MAB} = \widehat {BAC} - \widehat {MAC} = 90^\circ  - \widehat {MAC}\) (phụ nhau) (3)

Từ (1),(2) và (3) suy ra: \(\widehat {MAH} = \widehat {MAB} \Rightarrow \widehat {MAH} = \widehat {MAI}\)

Xét hai tam giác vuông \(\Delta AHM\) và \(\Delta AIM\) có:

AM (cạnh chung)

\(\widehat {MAH} = \widehat {MAI}\) (cmt)

\( \Rightarrow \;\Delta AHM = \Delta AIM\) (cạnh huyền-góc nhọn)

\( \Rightarrow AH = AI\) (hai cạnh tương ứng)

Lại có: \(MI\parallel AC (gt),AC \bot AB (gt) \Rightarrow MI \bot AB\).

Do đó \(BI < BM\,\,(4)\) (quan hệ giữa đường vuông góc và đường xiên)

Mặt khác:

\(AC = CM (gt) \,(5)\)

\(AI = AH (cmt) \,(6)\)

Cộng (6),(4),(5) vế theo vế ta được:

\(AI + BI + AC < AH + BM + CM\)

\( \Rightarrow AB + AC < AH + BC\).

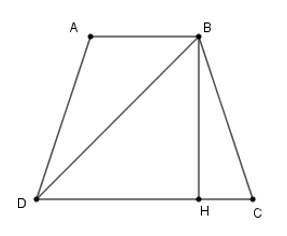
Kẻ \(BH \bot CD\) tại \(H.\)

Xét tam giác vuông \(BDH\), theo định lý Pytago, ta có \(B{D^2} = D{H^2} + B{H^2}\).

Xét tam giác vuông \(CBH\), theo định lý Pytago, ta có \(B{C^2} = C{H^2} + B{H^2}\).

Suy ra \(B{D^2} - B{C^2} = \left( {D{H^2} + B{H^2}} \right) - \left( {C{H^2} + B{H^2}} \right)\).

\( = D{H^2} - C{H^2} = \left( {DH + HC} \right)\left( {DH - HC} \right)\)\( = CD.AB\).