Câu hỏi:
3 năm trước
Cho tam giác $ABC$ cân tại $A$ . Trên các cạnh bên $AB$ , $AC$ lấy các điểm $M$ ,$N$ sao cho $BM$$ = CN$ .
Các điểm $M,N$ thỏa mãn điều kiện gì để $BM = MN = NC$ ?
Trả lời bởi giáo viên
Đáp án đúng: d
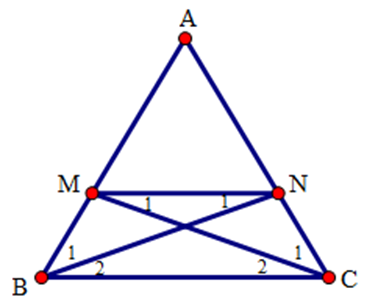
Ta có $BM = MN$ khi và chỉ khi \(\Delta MNB\) cân tại \(M \Rightarrow \) \(\widehat {{N_1}} = \widehat {{B_1}}\)\( \Leftrightarrow \widehat {{B_1}} = \widehat {{B_2}}\)(vì \(\widehat {{N_1}} = \widehat {{B_2}}\)) nên \(BN\) là phân giác góc $ABC$.
Tương tự $MN = NC$ khi và chỉ khi \(\Delta MNC\) cân tại \(N \Rightarrow \)\(\widehat {{C_1}} = \widehat {{C_2}}\) nên \(CM\) là phân giác góc \(ACB\) .
Như vậy, nếu $BN$ và $CM$ là các đường phân giác của tam giác $ABC$ thì $BM = MN = CN.$
Hướng dẫn giải:
Ta sử dụng tính chất tam giác cân để suy ra điều kiện của \(M,\,N\) .

