Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\). Trên \(BC\) lấy điểm \(M\) sao cho \(CM = CA\). Đường thẳng đi qua \(M\) và song song với \(CA\) cắt \(AB\) tại \(I\).
Chọn câu đúng.
Trả lời bởi giáo viên
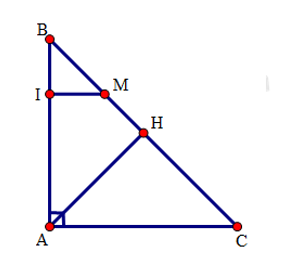
Xét tam giác \(AMC\) có: \(CM = AC(gt)\) nên tam giác \(AMC\) cân tại \(C\).
Suy ra \(\widehat {MAC} = \widehat {AMC\,}\,\,(1)\)
Xét tam giác AMH có: \(\widehat {MAH} = 90^\circ \widehat {- AMH}\) (hai góc phụ nhau) (2)
Xét tam giác ABC vuông tại A: \(\widehat {MAB} = \widehat {BAC} - \widehat {MAC} = 90^\circ - \widehat {MAC}\) (phụ nhau) (3)
Từ (1),(2) và (3) suy ra: \(\widehat {MAH} = \widehat {MAB} \Rightarrow \widehat {MAH} = \widehat {MAI}\)
Xét hai tam giác vuông \(\Delta AHM\) và \(\Delta AIM\) có:
AM (cạnh chung)
\(\widehat {MAH} = \widehat {MAI}\) (cmt)
\( \Rightarrow \;\Delta AHM = \Delta AIM\) (cạnh huyền-góc nhọn)
\( \Rightarrow AH = AI\) (hai cạnh tương ứng)
Lại có: \(MI\parallel AC (gt),AC \bot AB (gt) \Rightarrow MI \bot AB\).
Do đó \(BI < BM\,\,(4)\) (quan hệ giữa đường vuông góc và đường xiên)
Mặt khác:
\(AC = CM (gt) \,(5)\)
\(AI = AH (cmt) \,(6)\)
Cộng (6),(4),(5) vế theo vế ta được:
\(AI + BI + AC < AH + BM + CM\)
\( \Rightarrow AB + AC < AH + BC\).
Hướng dẫn giải:
Sử dụng:
Tính chất hai tam giác bằng nhau.
Quan hệ giữa đường vuông góc và đường xiên.

