Câu hỏi:
2 năm trước
Cho hình thang cân \(ABCD\left( {AB//CD} \right)\). Giả sử \(AB \le CD,\) chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: a
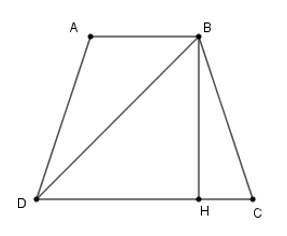
Kẻ \(BH \bot CD\) tại \(H.\)
Xét tam giác vuông \(BDH\), theo định lý Pytago, ta có \(B{D^2} = D{H^2} + B{H^2}\).
Xét tam giác vuông \(CBH\), theo định lý Pytago, ta có \(B{C^2} = C{H^2} + B{H^2}\).
Suy ra \(B{D^2} - B{C^2} = \left( {D{H^2} + B{H^2}} \right) - \left( {C{H^2} + B{H^2}} \right)\).
\( = D{H^2} - C{H^2} = \left( {DH + HC} \right)\left( {DH - HC} \right)\)\( = CD.AB\).
Hướng dẫn giải:
Sử dụng định lý Pytago trong tam giác vuông và hằng đẳng thức \({a^2} - {b^2} = \left( {a - b} \right)\left( {a + b} \right)\).
