Cho hình thang cân $ABCD$ ($AB$ //$CD$ ) có hai đường chéo cắt nhau tại $I$ , hai đường thẳng \(AD\) và \(BC\)  cắt nhau ở $K.$ Chọn khẳng định đúng.

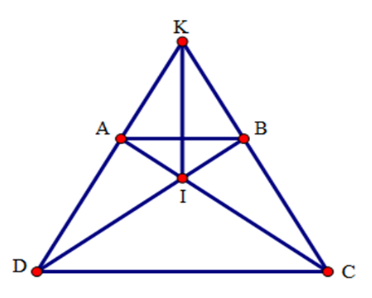
* Xét tam giác $ACD$ và tam giác $BDC$ có:

+$AD = BC$ (do $ABCD$ là hình thang cân)

+ $AC = BD$  (do $ABCD$ là hình thang cân)

  + $CD$ là cạnh chung

 Suy ra \(\Delta ACD = \Delta BDC\)(c.c.c). Suy ra \(\widehat {ACD} = \widehat {BDC}\) (hai góc tương ứng).

Xét tam giác $ICD$ có \(\widehat {ACD} = \widehat {BDC}\)(cmt), suy ra tam giác $ICD$ cân tại$I$ .Dođó $ID = IC\,\,\,\left( 1 \right)$

 Tam giác $KCD$ có hai góc ở đáy bằng nhau nên tam giác $KCD$ cân ở$K$ . Do đó $KC = KD$$\left( 2 \right)$

Từ $\left( 1 \right)$ và $\left( 2 \right)$ suy ra $KI$ là đường trung trực của$CD$    (*)

* Xét tam giác $ADB$ và tam giác $BCA$ có:

+ $AD = BC$  (cmt)

+ $AB$ là cạnh chung

+ $AC = BD$

Suy ra \(\Delta ADB = \Delta BCA\) (c.c.c). Suy ra \(\widehat {ABD} = \widehat {BAC}\) .

Xét tam giác $IAB$ có \(\widehat {ABD} = \widehat {BAC}\) nên tam giác $IAB$ cân tại$I$ . Do đó $IA = IB$$\left( 3 \right)$

Ta có:$KA = KD-AD$ ;$KB = KC-BC$ . Mà$KD = KC$ , $AD = BC$ , do đó $KA = KB$$\left( 4 \right)$

Từ $\left( 3 \right)$ và $\left( 4 \right)$ suy ra $KI$ là đường trung trực của$AB$ .   (**)

Từ (*) và (**) suy ra $KI$ là đường trung trực của hai đáy (đpcm)