Ứng dụng tích phân để giải một số bài toán thực tế
Kỳ thi ĐGTD ĐH Bách Khoa
Một viên gạch hoa hình vuông cạnh \(40\)cm. Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng

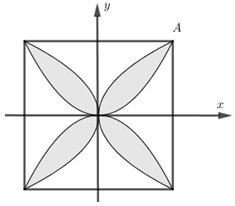
Chọn hệ trục tọa độ như hình vẽ:
Với $A\left( {20;20} \right)$, xét hình phẳng ở góc phân tư thứ nhất.
Hai Parabol có phương trình lần lượt là: $y = a{x^2}\,\,\left( {{P_1}} \right)$ và $x = a{y^2}\,\,\left( {{P_2}} \right)$
Do Parabol \(\left( {{P_1}} \right)\) qua điểm $A\left( {20;20} \right) \Rightarrow a = \dfrac{{20}}{{{{20}^2}}} = \dfrac{1}{{20}} \Rightarrow y = \dfrac{{{x^2}}}{{20}}$
Do Parabol \(\left( {{P_2}} \right)\) qua điểm $A\left( {20;20} \right) \Rightarrow a = \dfrac{{20}}{{{{20}^2}}} = \dfrac{1}{{20}} \Rightarrow x = \dfrac{{{y^2}}}{{20}} \Leftrightarrow y = \sqrt {20x} $
Diện tích phân tô đậm ở góc phần tư thứ nhất là:
$S = \int\limits_0^{20} {\left( {\sqrt {20x} - \dfrac{{{x^2}}}{{20}}} \right)dx} = \left( {\dfrac{2}{3}\sqrt {20{x^3}} - \dfrac{{{x^3}}}{{60}}} \right)\left| \begin{array}{l}^{20}\\_0\end{array} \right. = \dfrac{{400}}{3}.$
Một chất điểm đang chuyển động với vận tốc \({v_0} = 15\;{\rm{m/s}}\) thì tăng tốc với gia tốc \(a\left( t \right) = {t^2} + 4t\;\left( {{\rm{m/}}{{\rm{s}}^2}} \right)\). Tính quãng đường chất điểm đó đi được trong khoảng thời gian \(3\) giây kể từ lúc bắt đầu tăng vận tốc.
\(a\left( t \right) = {t^2} + 4t\) \( \Rightarrow v\left( t \right) = \int {a\left( t \right){\rm{d}}t} = \dfrac{{{t^3}}}{3} + 2{t^2} + C{\rm{ }}\)\(\left( {C \in \mathbb{R}} \right)\).
Mà \(v\left( 0 \right) = C = 15\) \( \Rightarrow v\left( t \right) = \dfrac{{{t^3}}}{3} + 2{t^2} + 15\).
Vậy $S = \int\limits_0^3 {\left( {\dfrac{{{t^3}}}{3} + 2{t^2} + 15} \right)dt} = 69,75\;{\rm{m}}$.
Bác Năm làm một cái cửa nhà hình parabol bằng gỗ có chiều cao từ mặt đất đến đỉnh là \(2,25\) mét, chiều rộng tiếp giáp với mặt đất là \(3\) mét. Giá tiền mỗi mét vuông gỗ là \(1500000\) đồng. Vậy số tiền bác Năm phải trả là:
Gọi phương trình parabol \(\left( P \right):y = a{x^2} + bx + c\). Do tính đối xứng của parabol nên ta có thể chọn hệ trục tọa độ \(Oxy\) sao cho \(\left( P \right)\) có đỉnh $I\left( {0;\dfrac{9}{4}} \right)\in Oy $ và đi qua hai điểm $A\left( { - \dfrac{3}{2};0} \right),B\left( {\dfrac{3}{2};0} \right)$ (như hình vẽ).
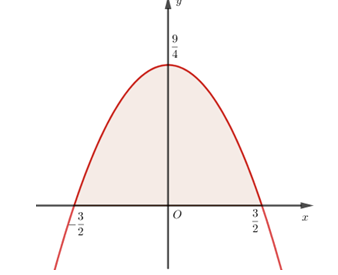
Ta có hệ phương trình: \(\left\{ \begin{array}{l}\dfrac{9}{4} = c,\left( {I \in \left( P \right)} \right)\\\dfrac{9}{4}a - \dfrac{3}{2}b + c = 0\left( {A \in \left( P \right)} \right)\\\dfrac{9}{4}a + \dfrac{3}{2}b + c = 0\left( {B \in \left( P \right)} \right)\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}c = \dfrac{9}{4}\\a = - 1\\b = 0\end{array} \right.\)
Vậy \(\left( P \right):y = - {x^2} + \dfrac{9}{4}\)
Dựa vào đồ thị, diện tích cửa parabol là:
\(S = \int\limits_{\frac{{ - 3}}{2}}^{\frac{3}{2}} {\left( { - {x^2} + \dfrac{9}{4}} \right){d}x} \)\( = 2\int\limits_0^{\frac{3}{2}} {\left( { - {x^2} + \dfrac{9}{4}} \right){d}x} \)$ = \left. {2\left( {\dfrac{{ - {x^3}}}{3} + \dfrac{9}{4}x} \right)} \right|_0^{\frac{9}{4}}$ \( = \dfrac{9}{2}{{\rm{m}}^2}\)
Số tiền phải trả là: \(\dfrac{9}{2}.1500000 = 6750000\) đồng
Một cổng chào có dạng hình parabol chiều cao 18m, chiều rộng chân đế 12m. Người ta căng sợi dây trang trí AB, CD nằm ngang đồng thời chia hình giới hạn bởi parabol thành ba phần có diện tích bằng nhau (xem hình vẽ bên). Tỉ số \(\dfrac{{AB}}{{CD}}\) bằng :
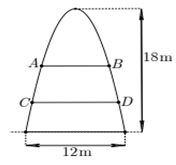
Gắn hệ trục tọa độ như hình vẽ :
Ta dễ dàng tìm được phương trình parabol là \(y = - \dfrac{1}{2}{x^2} + 18\)
Diện tích hình phẳng giới hạn bởi parabol và trục hoành là \(S = \int\limits_{ - 6}^6 {\left( { - \dfrac{1}{2}{x^2} + 18} \right)dx} = \left. {\left( { - \dfrac{{{x^3}}}{6} + 18x} \right)} \right|_{ - 6}^6 = 144.\)
Gọi \({x_A} = a \Rightarrow {y_A} = - \dfrac{1}{2}{a^2} + 18\)
\( \Rightarrow \) Phương trình đường thẳng AB : \(y = - \dfrac{1}{2}{a^2} + 18\)
và \({x_C} = c \Rightarrow {y_c} = - \dfrac{1}{2}{c^2} + 18\)
\( \Rightarrow \) Phương trình đường thẳng CD : \(y = - \dfrac{1}{2}{c^2} + 18\).
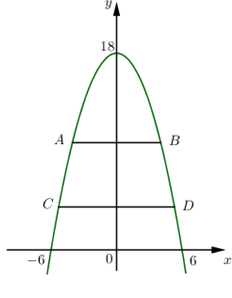
Diện tích hình phẳng giới hạn bởi parabol và đường thẳng AB là:
$\begin{array}{l}{S_1} = \int\limits_{ - a}^a {\left( { - \dfrac{1}{2}{x^2} + 18 + \dfrac{1}{2}{a^2} - 18} \right)dx} = \int\limits_{ - a}^a {\left( { - \dfrac{1}{2}{x^2} + \dfrac{1}{2}{a^2}} \right)dx} = \left. {\left( { - \dfrac{{{x^3}}}{6} + \dfrac{{{a^2}}}{2}x} \right)} \right|_{ - a}^a = - \dfrac{{{a^3}}}{6} + \dfrac{{{a^3}}}{2} - \left( {\dfrac{{{a^3}}}{6} - \dfrac{{{a^3}}}{2}} \right) = \dfrac{{2{a^3}}}{3}.\\{S_1} = \dfrac{1}{3}S \Rightarrow \dfrac{2}{3}{a^3} = \dfrac{1}{3}.144 = 48 \Rightarrow a = 2\sqrt[3]{9} \Rightarrow AB = 2a = 4\sqrt[3]{9}.\end{array}$
Diện tích hình phẳng giới hạn bởi parabol và đường thẳng CD là:
$\begin{array}{l}{S_2} = \int\limits_{ - c}^c {\left( { - \dfrac{1}{2}{x^2} + 18 + \dfrac{1}{2}{c^2} - 18} \right)dx} = \left. {\left( { - \dfrac{{{x^3}}}{6} + \dfrac{{{c^2}}}{2}x} \right)} \right|_{ - c}^c = - \dfrac{{{c^3}}}{6} + \dfrac{{{c^3}}}{2} - \left( {\dfrac{{{c^3}}}{6} - \dfrac{{{c^3}}}{2}} \right) = \dfrac{{2{c^3}}}{3}.\\{S_1} = \dfrac{2}{3}S \Rightarrow \dfrac{2}{3}{c^3} = \dfrac{2}{3}.144 = 96 \Rightarrow c = 2\sqrt[3]{{18}} \Rightarrow CD = 2c = 4\sqrt[3]{{18}}\\ \Rightarrow \dfrac{{AB}}{{CD}} = \dfrac{1}{{\sqrt[3]{2}}}\end{array}$
Một vật chuyển động trong $3$ giờ với vận tốc $v\,\,(km/h)$ phụ thuộc vào thời gian $t\,\,(h)$ có đồ thị vận tốc như hình bên. Trong khoảng thời gian $1$ giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có đỉnh $I(2;5)$ và có trục đối xứng song song với trục tung, khoảng thời gian còn lại của đồ thị là một đoạn thẳng song song với trục hoành. Tính quãng đường mà vật di chuyển được trong $3$ giờ đó
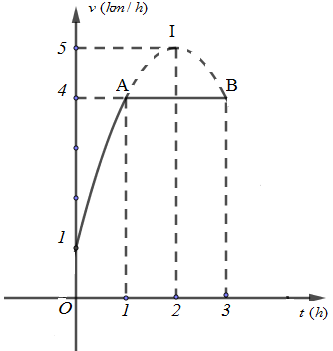
Gọi phương trình của vận tốc trong 1h đầu là: $v(t) = a\,{t^2} + bt + c\,\,(a \ne 0)$
Quan sát hình vẽ, ta thấy đồ thị hàm số có đỉnh $I(2;5)$ và đi qua điểm $A(1;4),\,\,\,(0;1)$.
Suy ra: $\left\{ \begin{array}{l} - \dfrac{b}{{2a}} = 2\\a{.2^2} + b.2 + c = 5\\c = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\b = - 4a\\4a + 2b + 1 = 5\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a = - 1\\b = 4\end{array} \right. \Rightarrow v(t) = - {t^2} + 4t + 1$
Quãng đường vật chuyển động trong 1 giờ đầu là:
$s = \int_0^1 {v(t)dt} = \int_0^1 {\left( { - {t^2} + 4t + 1} \right)dt} = \left. {\left( { - \dfrac{{{t^3}}}{3} + 2{t^2} + t} \right)} \right|_0^1 = - \dfrac{{{1^3}}}{3} + {2.1^2} + 1 - 0 = \dfrac{8}{3}\,(km)$
Trong 2h tiếp theo vật chuyển động thẳng đều với vận tốc \(4km/h\)
\( \Rightarrow \) Quãng đường đi được trong 2h tiếp theo là $8$ km.
Vậy quãng đường mà vật di chuyển được trong 3 giờ đó là: \(\dfrac{8}{3} + 8 = \dfrac{{32}}{3}\,\,\left( {km} \right)\)
Một ô tô chuyển động nhanh dần đều với vận tốc \(v\left( t \right) = 7t\) \(\left( {{\rm{m/s}}} \right)\). Đi được \(5\)\(\left( {\rm{s}} \right)\) người lái xe phát hiện chướng ngại vật và phanh gấp, ô tô tiếp tục chuyển động chậm dần đều với gia tốc \(a = - 35\) \(\left( {{\rm{m/}}{{\rm{s}}^{\rm{2}}}} \right)\). Tính quãng đường của ô tô đi được từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn?
Quãng đường ô tô đi được trong \(5\)\(\left( {\rm{s}} \right)\) đầu là ${s_1} = \int\limits_0^5 {7t{\rm{d}}t} = 7\left. {\dfrac{{{t^2}}}{2}} \right|_0^5 = 87,5$ (mét)
Phương trình vận tốc của ô tô khi người lái xe phát hiện chướng ngại vật là \({v_{\left( 2 \right)}}\left( t \right) = 35 - 35t\) (m/s). Khi xe dừng lại hẳn thì \({v_{\left( 2 \right)}}\left( t \right) = 0 \Leftrightarrow 35 - 35t = 0 \Leftrightarrow t = 1\)
Quãng đường ô tô đi được từ khi phanh gấp đến khi dừng lại hẳn là \({s_2} = \int\limits_0^1 {\left( {35 - 35t} \right){\rm{d}}t} \)\( = \left. {\left( {35t - 35\dfrac{{{t^2}}}{2}} \right)} \right|_0^1\)\( = 17,5\) (mét)
Vậy quãng đường của ô tô đi được từ lúc bắt đầu chuyển bánh cho đến khi dừng hẳn là \(s = {s_1} + {s_2}\)\( = 87,5 + 17,5\)\( = 105\) (mét)
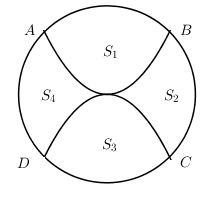
Sân trường THPT Chuyên Hà Giang có một bồn hoa hình tròn có tâm O. Một nhóm học sinh lớp 12 được giao thiết kế bồn hoa, nhóm này chia bồn hoa thành bốn phần, bởi hai đường Parabol có cùng đỉnh O và đối xứng nhau qua O. Hai đường Parabol này cắt đường tròn tại bốn điểm A, B, C, D tạo thành một hình vuông có cạnh bằng 4m (như hình vẽ). Phần diện tích \(S_1,S_3\) dùng để trồng hoa, phần diện tích \(S_2,S_4\) dùng để trồng cỏ (Diện tích được làm tròn đến hàng phần trăm). Biết kinh phí trồng hoa là \(150.000\) đồng/ \(m^2\), kinh phí trồng cỏ là \(100.000\) đồng/ \(m^2\). Hỏi cả trường cần bao nhiêu tiền để trồng bồn hoa đó? (Số tiền làm tròn đến hàng chục nghìn).
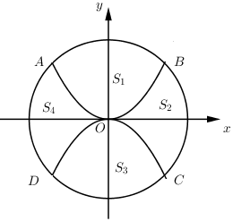
Gắn hệ trục tọa độ Oxy như hình vẽ, do ABCD là hình vuông cạnh 4m nên ta có \(A\left( { - 2;2} \right);B\left( {2;2} \right),C\left( {2; - 2} \right);D\left( { - 2; - 2} \right)\), từ đó ta dễ dàng viết được phương trình đường tròn là \({x^2} + {y^2} = 8\) và phương trình 2 parabol là \(y = \dfrac{1}{2}{x^2}\) và \(y = - \dfrac{1}{2}{x^2}\).
Ta có: S1 là diện tích hình phẳng giới hạn bởi đường tròn \({x^2} + {y^2} = 8\) và parabol (P): \(y = \dfrac{1}{2}{x^2}\)
\({S_1} = \int\limits_0^2 {\left( {\sqrt {8 - {x^2}} - \dfrac{1}{2}{x^2}} \right)dx} \) \(\Rightarrow {S_1} + {S_3} = 4\int\limits_0^2 {\left( {\sqrt {8 - {x^2}} - \dfrac{1}{2}{x^2}} \right)dx} = 15,23\left( {{m^2}} \right)\)
\({S_2} + {S_4} = \pi {\left( {2\sqrt 2 } \right)^2} - \left( {{S_1} + {S_3}} \right) = 9,90\left( {{m^2}} \right)\)
\( \Rightarrow \) Chi phí để trồng bồn hoa đó là: \(15,23.150 + 9,90.100 \approx 3270\) (nghìn đồng).
Một vật chuyển động trong 4 giờ với vận tốc $v$ (km/h) phụ thuộc vào thời gian $t\,$(h) có đồ thị là một phần của đường parabol có đỉnh I(1;1) và trục đối xứng song song với trục tung như hình bên. Tính quãng đường s mà vật di chuyển được trong 4 giờ kể từ lúc xuất phát.
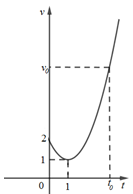
Gọi phương trình của đường parabol (P) cần tìm là : $y = a{x^2} + bx + c,a \ne 0$
Parabol đi qua điểm $\left( {0;2} \right) \Rightarrow 2 = a{.0^2} + b.0 + c \Rightarrow c = 2$ .
Parabol có đỉnh $I\left( {1;1} \right) \Rightarrow \left\{ \begin{array}{l} - \dfrac{b}{{2a}} = 1\\a{.1^2} + b.1 + 2 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b + 2a = 0\\a + b = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = - 2\end{array} \right.$
Vậy $(P):\,\,y = {x^2} - 2x + 2$ .
Quãng đường vật di chuyển được trong 4 giờ kể từ lúc xuất phát:
$s = \int\limits_0^4 {v(t)dt} = \int\limits_0^4 {({t^2} - 2t + 2)dt} = \left. {\left( {\dfrac{{{t^3}}}{3} - {t^2} + 2t} \right)} \right|_0^4 = \dfrac{{{4^3}}}{3} - {4^2} + 2.4 = \dfrac{{40}}{3}$
Một chất điểm A xuất phát từ O, chuyển động thẳng với vận tốc biến thiên theo thời gian bởi quy luật \(v\left( t \right) = \dfrac{1}{{100}}{t^2} + \dfrac{{13}}{{10}}t\left( {m/s} \right)\), trong đó t (giây) là khoảng thời gian tính từ lúc A bắt đầu chuyển động. từ trạng thái nghỉ, một chất điểm B cũng xuất phát từ O, chuyển động thẳng cùng hướng với A nhưng chậm hơn 10 giây so với A và có gia tốc bằng \(a\left( {m/{s^2}} \right)\) (\(a\) là hằng số). Sau khi B xuất phát được 15 giây thì đuổi kịp A. Vận tốc của B tại thời điểm đuổi kịp A bằng
Bước 1: Tìm $v_B(t)$
Ta có \({v_B}\left( t \right) = \int {adt} = at + C,{v_B}\left( 0 \right) = 0\)
\( = > C = 0 = > {v_B}\left( t \right) = at\)
Bước 2: Tính quãng đường A đi được trong 25 giây
Quãng đường chất điểm A đi được trong 25 giây là
\({S_A} = \int\limits_0^{25} {\left( {\dfrac{1}{{100}}{t^2} + \dfrac{{13}}{{10}}t} \right)dt} \) \( = \left. {\left( {\dfrac{1}{{300}}{t^3} + \dfrac{{13}}{{60}}{t^2}} \right)} \right|_0^{25} = \dfrac{{375}}{2}\)
Bước 3: Tính quãng đường B đi được trong 15 giây
Quãng đường chất điểm B đi được trong 15 giây là
\({S_B} = \int\limits_0^{15} {at} .dt = \left. {\dfrac{{a{t^2}}}{2}} \right|_0^{15} = \dfrac{{225a}}{2}\)
Bước 4: Tìm a và $v_B(15)$
Ta có: \(\dfrac{{375}}{2} = \dfrac{{225a}}{2} \Leftrightarrow a = \dfrac{5}{3}\)
Vận tốc của B tại thời điểm đuổi kịp A là \(v_B\left( {15} \right) = \dfrac{5}{3}.15 = 25\left( {m/s} \right)\)
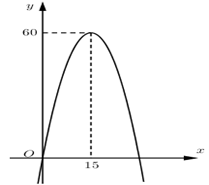
Một xe mô tô phân khối lớn sau khi chờ đèn đỏ đã bắt đầu phóng nhanh với vận tốc tăng liên tục được biểu thị bằng đồ thị là đường Parabol (hình vẽ). Biết rằng sau $15$ giây thì xe đạt đến vận tốc cao nhất $60{\rm{ }}m/s$ và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu đến lúc đạt vận tốc cao nhất thì quãng đường xe đi được là bao nhiêu?
Gọi phương trình parabol biểu diễn cho vận tốc của vật là \(v\left( t \right) = a{t^2} + bt + c\,\,\left( {a \ne 0} \right)\)
Đỉnh của parabol có tọa độ \(\left( {15;60} \right) \Rightarrow - \dfrac{b}{{2a}} = 15\,\,\left( 1 \right)\)
Parabol đi qua điểm \(\left( {15;60} \right)\) và điểm \(\left( {0;0} \right) \Rightarrow \left\{ \begin{array}{l}225a + 15b + c = 60\\c = 0\end{array} \right.\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow \left\{ \begin{array}{l}a = \dfrac{{ - 4}}{{15}}\\b = 8\\c = 0\end{array} \right. \Rightarrow v\left( t \right) = - \dfrac{4}{{15}}{t^2} + 8t\)
Dựa vào đồ thị ta thấy vận đạt vận tốc cao nhất tại $t{\rm{ }} = {\rm{ }}15s$ .
Khi đó quãng đường đi được từ lúc bắt đầu đến lúc vận tốc cao nhất là: \(S = \int\limits_0^{15} {\left( { - \dfrac{4}{{15}}{t^2} + 8t} \right)dt} = 600\,\,\left( m \right)\)
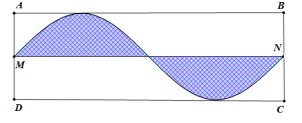
Ông A có một mảnh đất hình chữ nhật \(ABCD\) có \(AB = 2\pi \,\left( m \right),\,\,AD = 5\,\left( m \right)\). Ông muốn trồng hoa trên giải đất có giới hạn bởi hai đường trung bình $MN$ và đường hình $sin$ (như hình vẽ). Biết kinh phí trồng hoa là $100.000$ đồng $/{\rm{ }}{m^2}$ . Hỏi ông A cần bao nhiêu tiền để trồng hoa trên giải đất đó?
Gắn hệ trục tọa độ $Oxy$ như hình vẽ:
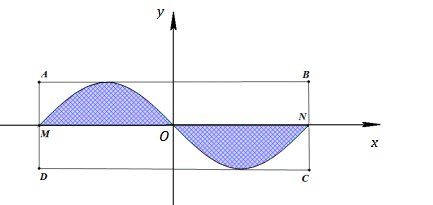
Dựa vào hình vẽ ta thấy đường $sin$ có chu kì bằng \(AB = 2\pi \) và biên độ bằng \(AM = \dfrac{1}{2}AD = \dfrac{5}{2}\) Đường hình $sin$ có phương trình \(y = - \dfrac{5}{2}\sin x\).
Đường thẳng $BC$ có phương trình \(x = \pi \).
Xét hình phẳng giới hạn bởi đồ thị hàm số \(y = - \dfrac{5}{2}\sin x\), trục $Ox$ , đường thẳng \(x = 0;\,\,x = \pi \) có $S = \int\limits_0^\pi {\left| { - \dfrac{5}{2}\sin x} \right|} dx = \dfrac{5}{2}\int\limits_0^\pi {\sin xdx} = - \left. {\dfrac{5}{2}\cos x} \right|_0^\pi = \dfrac{5}{2} + \dfrac{5}{2} = 5\,\,\left( m \right)$ .
\( \Rightarrow \) Diện tích giải đất ông A dùng để trồng hoa là \(2S = 10\,\,\left( {{m^2}} \right)\) , do đó kinh phí để trồng hoa là $1.000.000$ đồng.
Một ô tô đang đứng và bắt đầu chuyển động theo một đường thẳng với gia tốc \(a\left( t \right) = 6 - 3t\,\,\left( {m/{s^2}} \right)\), trong đó \(t\) là khoảng thời gian tính bằng giây kể từ lúc ô tô bắt đầu chuyển động. Hỏi quãng đường ô tô đi được kể từ lúc bắt đầu chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là:
Ta có \(v\left( t \right) = \int {a\left( t \right)dt} = \int {\left( {6 - 3t} \right)dt} = 6t - \dfrac{{3{t^2}}}{2} + C\).
Theo bài ra ta có: Ô tô đang đứng yên và bắt đầu chuyển động, do đó \(v\left( 0 \right) = 0\) \( \Rightarrow C = 0\).
Khi đó ta có \(v\left( t \right) = 6t - \dfrac{3}{2}{t^2}\), đây là một parabol có bề lõm hướng xuống, đạt giá trị lớn nhất tại \(t = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 6}}{{2.\left( { - \dfrac{3}{2}} \right)}} = 2\).
Vậy quãng đường ô tô đi được từ khi chuyển động đến khi vận tốc của ô tô đạt giá trị lớn nhất là:
\(S = \int\limits_0^2 {v\left( t \right)dt} = \int\limits_0^2 {\left( {6t - \dfrac{3}{2}{t^2}} \right)dt} = 8\,\,\left( m \right).\)
Một tập đoàn định đầu tư vào hai dự án. Giả sử dự án đầu tư đầu có tốc độ sinh lợi nhuận là \({P_1}\left( t \right) = 50 + {t^2}\) (triệu đồng/năm), dự án thứ hai có tốc độ sinh lợi nhuận là \({P_2}\left( t \right) = 200 + 5t\) ( triệu đồng/năm). Sau t năm thì tốc độ sinh lợi nhuận của dự án hai bằng một nửa dự án một. Trong khoảng thời gian trên, chênh lệch lợi nhuận của hai dự án là bao nhiêu?
Bước 1: Tìm t
Tốc độ sinh lợi nhuận của dự án hai bằng một nửa dự án một khi
\({P_1} = 2{P_2} \Leftrightarrow 50 + {t^2} = 400 + 10t\)
\( \Leftrightarrow {t^2} - 10t - 350 = 0 \Leftrightarrow t = 5 + 5\sqrt {15} \)
Bước 2: Sử dụng tích phân để tính chênh lệch lợi nhuận thực tế
Chênh lệch lợi nhuận thực tế giữa 2 dự án trong khoảng thời gian đó là
\(\begin{array}{l}L = \int\limits_0^{5 + 5\sqrt {15} } {\left[ {{P_2}\left( t \right) - {P_1}\left( t \right)} \right]dt} \\ = \int\limits_0^{5 + 5\sqrt {15} } {\left( {350 + 10t - {t^2}} \right)} = 6674,6\end{array}\)
Một chất điểm chuyển động thẳng với vận tốc \(v\left( t \right) = 2t + 3\,\left( {m/s} \right)\), với \(t\) là thời gian tính bằng giây \(\left( s \right)\) từ lúc chất điểm bắt đầu chuyển động. Tính quãng đường chất điểm đi được trong khoảng thời gian từ giây thứ nhất đến giây thứ năm.
Ta có: \(v\left( t \right) = 2t + 3\,\,\left( {m/s} \right)\)
Khi đó quãng đường của vật được tính từ giây thứ nhất đến giây thứ năm là:
\(s\left( t \right) = \int\limits_1^5 {\left( {2t + 3} \right)dt} \) \( = \left. {\left( {{t^2} + 3t} \right)} \right|_1^5\) \( = {5^2} + 3.5 - 1 - 3 = 36\,\,(m).\)
Một đám vi trùng tại ngày thứ \(t\) có số lượng \(N\left( t \right)\), biết rằng \(N'\left( t \right) = \dfrac{{4000}}{{1 + 0,5t}}\) và lúc đầu đám vi trùng có \(250000\) con. Hỏi số lượng vi trùng tại ngày thứ $10$ (lấy theo phần nguyên) là bao nhiêu?
Ta có: \( N(t)=\int {N'(t)dt} = \int {\dfrac{{4000}}{{0,5t + 1}}dt} \)\(= \dfrac{{4000}}{{0,5}}\ln \left| {0,5t + 1} \right| + C = 8000\ln \left| {0,5t + 1} \right| + C\).
Với \(t = 0\) thì \(250000 = 8000\ln 1 + C \)\(\Leftrightarrow C = 250000\).
Vậy \(N\left( t \right) = 8000\ln \left| {0,5t + 1} \right| + 250000 \)\(\Rightarrow N\left( {10} \right) \approx 264334\)
Một xe lửa chuyển động chậm dần đều và dừng lại hẳn sau $20 \mathrm{~s}$ kể từ lúc bắt đầu hãm phanh. Trong thời gian đó xe chạy được $120 \mathrm{~m}$. Biết công thức tính vận tốc của chuyển động biến đổi đều là $v=v_{0}+a t ;$ trong đó $a\left(\mathrm{~m} / \mathrm{s}^{2}\right)$ là gia tốc, $v(\mathrm{~m} / \mathrm{s})$ là vận tốc tại thời điểm $t(s)$. Hãy tính vận tốc $v_{0}$ của xe lửa lúc bắt đầu hãm phanh
$12 \mathrm{~m} / \mathrm{s}$
$12 \mathrm{~m} / \mathrm{s}$
$12 \mathrm{~m} / \mathrm{s}$
Bước 1: Tìm a
Tại thời điểm $t=20(s), v(20)=0$ nên $v_{0}+20 a=0 \Rightarrow a=-\dfrac{v_{0}}{20}$
Do đó, $v(t)=v_{0}-\dfrac{v_{0}}{20} t$
Bước 2: Tính \(\int\limits_0^{20} {v\left( t \right)dt} \)
Mặt khác, $v(t)=s^{\prime}(t) \Rightarrow \int_{0}^{20} v(t) \mathrm{d} t=\int_{0}^{20} s^{\prime}(t) \mathrm{d} t=\left.s(t)\right|_{0} ^{20}=s(20)-s(0)=120$
Bước 3: Tính \({v_0}\)
Suy ra, $\int_{0}^{20}\left(v_{0}-\dfrac{v_{0}}{20} t\right) \mathrm{d} t=\left.120 \Rightarrow\left(v_{0} t-\dfrac{v_{0}}{40} t^{2}\right)\right|_{0} ^{20}=120$
Từ đó ta có phương trình $20 v_{0}-10 v_{0}=120 \Rightarrow v_{0}=12(\mathrm{~m} / \mathrm{s})$
Một chiếc xe đua \({F_1}\) đạt tới vận tốc lớn nhất là \(360\,\,km/h\). Đồ thị bên biểu thị vận tốc \(v\) của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu là một phần của một parabol định tại gốc tọa độ \(O\), giây tiếp theo là đoạn thẳng và sau đúng ba giây thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trực tung biểu thị 10 m/s và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó xe đã đi được quãng đường là bao nhiêu?
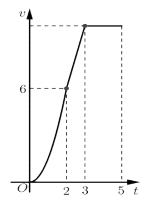
Trong 2 giây đầu, \({v_1} = a{t^2}\), lại có khi \(t = 2\,\,\left( s \right) \Rightarrow {v_1} = 60\,\,\left( {m/s} \right)\) nên \(60 = a{.2^2} \Leftrightarrow a = 15\), suy ra \({v_1} = 15{t^2}\).
Quãng đường vật đi được trong 2 giây đầu là \({s_1} = \int\limits_0^2 {{v_1}\left( t \right)dt} = \int\limits_0^2 {15{t^2}dt} = 40\,\,\left( m \right)\).
Trong giây tiếp theo, \({v_2} = mt + n\).
Ta có \(\left\{ \begin{array}{l}t = 2 \Rightarrow v = 60\\t = 3 \Rightarrow v = 360km/h = 100m/s\end{array} \right.\), nên ta có hệ phương trình \(\left\{ \begin{array}{l}2m + n = 60\\3m + n = 100\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 40\\n = - 20\end{array} \right.\) \( \Rightarrow {v_2}\left( t \right) = 40t - 20\).
Quãng đường vật đi được trong giây tiếp theo là \({s_2} = \int\limits_2^3 {{v_2}\left( t \right)dt} = \int\limits_2^3 {\left( {40t - 20} \right)dt} = 80\,\,\left( m \right)\).
Trong 2 giây cuối, \({v_3} = 100\,\,\left( {m/s} \right)\).
Quãng đường vật đi được trong 2 giây cuối là \({s_3} = \int\limits_3^5 {{v_3}\left( t \right)dt} = \int\limits_3^5 {100dt} = 200\,\,\left( m \right)\).
Vậy trong 5 giây đó xe đã đi được quãng đường là: \(40 + 80 + 200 = 320\,\,\left( m \right)\).

