Phương trình \({4^{2x + 5}} = {2^{2 - x}}\) có nghiệm là:
${4^{2{\rm{x}} + 5}} = {2^{2 - x}} \Leftrightarrow {2^{4{\rm{x}} + 10}} = {2^{2 - x}} \Leftrightarrow 4{\rm{x}} + 10 = 2 - x \Leftrightarrow 5{\rm{x}} = - 8 \Leftrightarrow x = \dfrac{{ - 8}}{5}$
Tổng các nghiệm của phương trình \({3^{{x^4} - 3{x^2}}} = 81\)
\({3^{{x^4} - 3{x^2}}} = 81 = {3^4} \Leftrightarrow {x^4} - 3{x^2} - 4 = 0 \Leftrightarrow {x^2} = 4 \Leftrightarrow x = \pm 2\)
Tổng các nghiệm sẽ bằng $0$.
Tìm nghiệm của phương trình \(\dfrac{{{3^{2x - 6}}}}{{27}} = {\left( {\dfrac{1}{3}} \right)^x}.\)
\(\dfrac{{{3^{2x - 6}}}}{{27}} = {\left( {\dfrac{1}{3}} \right)^x} \Leftrightarrow {3^{2x - 6}} = {3^3}{.3^{ - x}} \Leftrightarrow {3^{2x - 6}} = {3^{3 - x}} \Leftrightarrow 2x - 6 = 3 - x \Leftrightarrow x = 3\)
Tìm nghiệm của phương trình \({9^{\sqrt {x - 1} }} = {e^{\ln 81}}\)
\({e^{\ln 81}} = 81 = {9^2}\)
Điều kiện: $x \ge 1$.
Suy ra \(\sqrt {x - 1} = 2 \Leftrightarrow x - 1 = 4 \Rightarrow x = 5\)
Giải phương trình \({4^x} = {8^{x - 1}}\)
\({4^x} = {8^{x - 1}} \Leftrightarrow {2^{2x}} = {2^{3\left( {x - 1} \right)}} \Leftrightarrow 2x = 3\left( {x - 1} \right) \Leftrightarrow x = 3\)
Tìm tập hợp tất cả các nghiệm của phương trình ${2^{{x^2} + x - 1}} = \dfrac{1}{2}$.
\({2^{{x^2} + x - 1}} = \dfrac{1}{2} \Leftrightarrow {2^{{x^2} + x - 1}} = {2^{ - 1}} \Leftrightarrow {x^2} + x - 1 = - 1 \Leftrightarrow {x^2} + x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\end{array} \right.\)
Tìm giá trị của $a$ để phương trình ${\left( {2 + \sqrt 3 } \right)^x} + \left( {1 - a} \right){\left( {2 - \sqrt 3 } \right)^x} - 4 = 0$ có 2 nghiệm phân biệt thỏa mãn:${x_1} - {x_2} = {\log _{2 + \sqrt 3 }}3$, ta có a thuộc khoảng:
Ta có ${\left( {2 + \sqrt 3 } \right)^x}{\left( {2 - \sqrt 3 } \right)^x} = 1 \Rightarrow {\left( {2 - \sqrt 3 } \right)^x} = \dfrac{1}{{{{\left( {2 + \sqrt 3 } \right)}^x}}}$.
Đặt $t = {\left( {2 + \sqrt 3 } \right)^x}{\rm{ }}\left( {t > 0} \right)$, phương trình đã cho trở thành $t + \dfrac{{1 - a}}{t} - 4 = 0 \Leftrightarrow {t^2} - 4t + 1 - a = 0$(*)
Phương trình đã cho có 2 nghiệm phân biệt khi và chỉ khi phương trình (*) có 2 nghiệm dương phân biệt $ \Leftrightarrow \left\{ \begin{array}{l}\Delta = 3 + a > 0\\{t_1} + {t_2} = 4 > 0\\{t_1}{t_2} = 1 - a > 0\end{array} \right. \Leftrightarrow - 3 < a < 1$
Ta có ${x_1} - {x_2} = {\log _{2 + \sqrt 3 }}3 \Leftrightarrow {\left( {2 + \sqrt 3 } \right)^{{x_1} - {x_2}}} = 3 \Leftrightarrow \dfrac{{{{\left( {2 + \sqrt 3 } \right)}^{{x_1}}}}}{{{{\left( {2 + \sqrt 3 } \right)}^{{x_2}}}}} = 3 \Leftrightarrow \dfrac{{{t_1}}}{{{t_2}}} = 3$
Vì ${t_1} + {t_2} = 4$ nên điều này xảy ra khi và chỉ khi phương trình (*) có 2 nghiệm $t = 3$ và $t = 1$.
Khi đó $1 – a = 3.1 = 3 ⇔ a = –2$.
Trong 4 đáp án chỉ có B là đúng.
Tìm tập nghiệm S của phương trình: ${4^{x + 1}} + {4^{x - 1}} = 272$
Thử lần lượt từng đáp án ta thấy $x = 3$ là nghiệm của phương trình
Giải phương trình \(\sqrt {{3^x} + 6} = {3^x}\) có tập nghiệm bằng:
Đặt
\(\begin{array}{l}t = {3^x},t > 0 \Rightarrow \sqrt {t + 6} = t \to t + 6 = {t^2} \Rightarrow \left[ \begin{array}{l}t = - 2(l)\\t = 3\end{array} \right.\\t = 3 \Rightarrow {3^x} = 3 \Rightarrow x = 1\end{array}\)
Tìm tích các nghiệm của phương trình \({(\sqrt 2 - 1)^x} + {(\sqrt 2 + 1)^x} - 2\sqrt 2 = 0\)
Đặt $t = {\left( {\sqrt 2 - 1} \right)^x}\left( {t > 0} \right)$ phương trình có dạng $t + \dfrac{1}{t} = 2\sqrt 2 \Leftrightarrow {t^2} - 2\sqrt 2 t + 1 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{t = \sqrt 2 + 1} (tm)\\{t = \sqrt 2 - 1} (tm) \end{array}} \right.$
Khi đó
$\begin{array}{l}t = \sqrt 2 + 1 \Rightarrow x = - 1\\t = \sqrt 2 - 1 \Rightarrow x = 1\end{array}$
Suy ra tích các nghiệm bằng $-1$.
Tìm $m$ để phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm $x \in \left( {1;3} \right)$ .
Đặt $t = {2^x};x \in \left( {1;3} \right) \Rightarrow t = {2^x} \in \left( {2;8} \right)$
Xét hàm số \(y = {t^2} - 8t + 3\) trên \((2;8)\) có:
$y' = 2t - 8;$ $y' = 0 \Leftrightarrow 2t - 8 = 0 \Leftrightarrow t = 4\in (2;8)$
Bảng biến thiên:
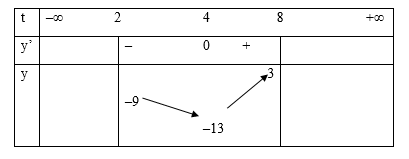
Căn cứ bảng biến thiên:
Phương trình \({4^x} - {\text{ }}{2^{x{\text{ }} + {\text{ }}3}} + {\text{ }}3{\text{ }} = {\text{ }}m\) có đúng 2 nghiệm \(x \in \left( {1;3} \right) \Leftrightarrow - 13 < m < - 9\)
Tìm tập hợp tất cả các tham số $m$ sao cho phương trình ${4^{{x^2} - 2x + 1}} - m{.2^{{x^2} - 2x + 2}} + 3m - 2 = 0$ có 4 nghiệm phân biệt.
Đặt $t = {2^{{x^2} - 2x + 1}} \ge 1$, phương trình đã cho trở thành ${t^2} - 2mt + 3m - 2 = 0{\rm{ }}\left( * \right)$
Với $t = 1$ ta tìm được 1 giá trị của $x$
Với $t > 1$ ta tìm được 2 giá trị của $x$
Do đó, phương trình đã cho có 4 nghiệm phân biệt
⇔ Phương trình (*) có 2 nghiệm phân biệt lớn hơn $1$
$\left\{ \begin{array}{l}\Delta ' = {m^2} - \left( {3m - 2} \right) > 0\\\left( {{t_1} - 1} \right) + \left( {{t_2} - 1} \right) > 0\\\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 2 > 0\\{t_1} + {t_2} > 2\\{t_1}{t_2} - \left( {{t_1} + {t_2}} \right) + 1 > 0\end{array} \right. \\ \Leftrightarrow \left\{ \begin{array}{l}{m^2} - 3m + 2 > 0\\2m > 2\\3m - 2 - 2m + 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 2\\m < 1\end{array} \right.\\m > 1\end{array} \right.$
⇔ $m > 2$
Các giá trị thực của tham số $m$ để phương trình : ${12^x} + \left( {4 - m} \right){.3^x} - m = 0$ có nghiệm thuộc khoảng $\left( { - 1;0} \right)$ là:
- Từ các đáp án đã cho, ta thấy giá trị $m=2$ không thuộc đáp án C nên ta thử $m=2$ có thỏa mãn bài toán hay không sẽ loại được đáp án.
Thử với $m=2$ ta được phương trình : \({12^x} + {2.3^x} - 2 = 0;\) \( f( - 1) = \dfrac{{ - 5}}{4};\) \(f(0) = 1\) \( \Rightarrow f(0).f( - 1) < 0\)
Do đó, phương trình có nghiệm trong khoảng $(-1;0)$, mà đáp án C không chứa $m=2$ nên loại C.
- Lại có giá trị $m=3$ thuộc đáp án C nhưng không thuộc hai đáp án A và D nên nếu kiểm tra $m=3$ ta có thể loại tiếp được đáp án.
Thử với $m=3$ ta được phương trình : \({12^x} + {3^x} - 3 = 0;\) \(f( - 1) = \dfrac{{ - 31}}{{12}};\) \(f(0) = - 1\) \( \Rightarrow f(0).f( - 1) > 0\)
Mà hàm số này đồng biến khi $m=3$ nên $f(x)<0,\forall x\in (-1;0)$, suy ra phương trình $f(x)=0$ sẽ không có nghiệm trong $(-1;0)$, loại B.
- Cuối cùng, ta thấy giá trị $m=1$ thuộc đáp án A và không thuộc đáp án D nên ta sẽ thử $m=1$ để loại đáp án.
Thử với $m=1$ ta được phương trình : \({12^x} + {3.3^x} - 1 = 0;\) \(f( - 1) = \dfrac{{ - 11}}{{12}};\,f(0) = 3\) \( \Rightarrow f(0).f( - 1) < 0\)
Do đó phương trình $f(x)=0$ sẽ có nghiệm trong $(-1;0)$ nên loại D và chọn A.
Tìm giá trị của tham số $m$ để phương trình ${9^x} - m{.3^{x + 2}} + 9m = 0$ có hai nghiệm phân biệt ${x_1};{x_2}$ thỏa mãn ${x_1} + {x_2} = 3$
Phương trình tương đương với: \({3^{2x}} - 9m{.3^x} + 9m = 0\) (*)
Đặt ${3^x} = a$ với $a > 0$ phương trình thành: ${a^2} - 9m.a + 9m = 0$
Giả sử phương trình có 2 nghiệm ${x_1}$ và ${x_2}$ thì \({3^{{x_1}}};{3^{{x_2}}}\) lần lượt là nghiệm của (*)
Suy ra: \({3^{{x_1}}}{.3^{{x_2}}} = 9m \Leftrightarrow {3^{{x_1} + {x_2}}} = 9m \Leftrightarrow {x_1} + {x_2} = {\log _3}9m = 3 \Rightarrow 9m = 27 \Leftrightarrow m = 3\)
Tìm tập hợp tất cả các giá trị của tham số thực $m$ để phương trình sau có 2 nghiệm phân biệt: \({9^{1 - x}} + 2(m - 1){3^{1 - x}} + 1 = 0\)
Thử với $m = -1$ ta được phương trình:
${\left( {{3^{1 - x}}} \right)^2} - {4.3^{1 - x}} + 1 = 0$ phải có 2 nghiệm $3^{1-x}$ đều dương và 2 nghiệm đó là \(2 - \sqrt 3 \) và $2 + \sqrt 3 $.
Vậy $m = - 1$ thỏa mãn nên ta loại được A; B; D
Cho số thực $x$ thỏa mãn \(2 = {5^{{{\log }_3}x}}\) . Mệnh đề nào sau đây đúng?
\(2 = {5^{{{\log }_3}x}} \Leftrightarrow {\log _5}2 = {\log _3}x \Leftrightarrow \dfrac{{{{\log }_5}x}}{{{{\log }_5}3}} = {\log _5}2 \)
$\Leftrightarrow \dfrac{{{{\log }_5}x}}{{{{\log }_5}2}} = {\log _5}3 \Leftrightarrow {\log _5}3 = {\log _2}x \Leftrightarrow {\log _3}5 = {\log _x}2$
Suy ra $2 = {x^{{{\log }_3}5}}$
Biết phương trình \({9^x} - {2^{x + \frac{1}{2}}} = {2^{x + \frac{3}{2}}} - {3^{2x - 1}}\) có nghiệm là $a$. Tính giá trị của biểu thức \(P = a + \dfrac{1}{2}{\log _{\frac{9}{2}}}2\) .
Phương trình trên tương đương với
\({3^{2x - 2}} = {2^{x - \frac{3}{2}}} \) \(\Leftrightarrow {9^{x - 1}} = {2^{x - 1}}{.2^{\frac{{ - 1}}{2}}}\) \( \Leftrightarrow {(\dfrac{9}{2})^{x - 1}} = {2^{\frac{{ - 1}}{2}}} \)
$\Leftrightarrow x - 1 = {\log _{\frac{9}{2}}}{2^{\frac{{ - 1}}{2}}} $ $\Leftrightarrow x = 1 - \dfrac{1}{2}{\log _{\frac{9}{2}}}2$
Suy ra \(x + \dfrac{1}{2}{\log _{\frac{9}{2}}}2 = 1\)
Biết rằng phương trình ${2^{{x^2} - 1}} = {3^{x + 1}}$ có hai nghiệm là $a$ và $b$. Khi đó $a+ b + ab$ có giá trị bằng
Lấy $\ln $ hai vế ta được:
$\begin{array}{l}({x^2} - 1)\ln 2 = (x + 1)\ln 3 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\(x - 1)\ln 2 = \ln 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x - 1 = \dfrac{{\ln 3}}{{\ln 2}} = {\log _2}3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = 1 + {\log _2}3\end{array} \right.\end{array}$
Nếu $a = - 1;b = 1 + lo{g_2}3 \Rightarrow a + b + ab = \; - 1$.
Tìm các giá trị $m$ để phương trình \({2^{x + 1}} = m{.2^{x + 2}} - {2^{x + 3}}\) luôn thỏa, \(\forall x \in \mathbb{R}\).
\({2^{x + 1}} = m{.2^{x + 2}} - {2^{x + 3}}{\rm{ }} \Leftrightarrow {2^{x + 1}} = m{.2^{x + 1 + 1}} - {2^{x + 1 + 2}} \)
$\Leftrightarrow {2^{x + 1}} = m{.2.2^{x + 1}} - {2^2}{.2^{x + 1}} \Leftrightarrow {2^{x + 1}} = (2m - 4){2^{x + 1}}$
\( \Leftrightarrow 2m - 4 = 1 \Leftrightarrow m = \dfrac{5}{2}\)
Số nghiệm thực phân biệt của phương trình ${4^{{x^2}}} - {5.2^{{x^2}}} + 4 = 0$ là
$\begin{array}{l}{4^{{x^2}}} - {5.2^{{x^2}}} + 4 = 0 \Leftrightarrow {\left( {{2^{{x^2}}}} \right)^2} - {5.2^{{x^2}}} + 4 = 0 \Leftrightarrow \left( {{2^{{x^2}}} - 4} \right)\left( {{2^{{x^2}}} - 1} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}{2^{{x^2}}} = 4\\{2^{{x^2}}} = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}{x^2} = 2\\{x^2} = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \pm \sqrt 2 \\x = 0\end{array} \right.\end{array}$
