Khảo sát hàm đa thức bậc bốn trùng phương
Kỳ thi ĐGTD ĐH Bách Khoa
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a > 0} \right)$. Chọn kết luận đúng:
Vì $a > 0$ nên $\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to - \infty } y = + \infty $.
Cho hàm số $y = a{x^4} + b{x^2} + c$ có bảng biến thiên như hình vẽ. Chọn kết luận đúng:
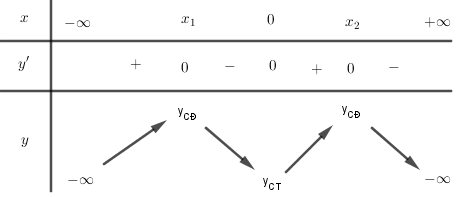
Từ bảng biến thiên ta thấy $\mathop {\lim }\limits_{x \to \pm \infty } y = - \infty $ nên $a < 0$.
Hàm số bậc bốn trùng phương có $3$ cực trị nếu:
Hàm số bậc bốn trùng phương có $3$ cực trị nếu và chỉ nếu phương trình $y' = 0$ có ba nghiệm phân biệt.
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a > 0} \right)$ có ba cực trị. Nếu ${y_{CD}} < 0$ thì:
Dễ thấy hàm số bậc bốn trùng phương có cực đại, cực tiểu thì ${y_{CT}} < {y_{CD}}$ nên ${y_{CD}} < 0 \Rightarrow {y_{CT}} < 0$.
Hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị nếu và chỉ nếu:
Ta có: $y' = 4a{x^3} + 2bx = 2x\left( {2a{x^2} + b} \right)$.
Hàm số có $1$ cực trị $ \Leftrightarrow y' = 0$ có $1$ nghiệm duy nhất hay $y'=0$ vô nghiệm hoặc có nghiệm kép
\( \Leftrightarrow \left[ \begin{array}{l}ab > 0\\b \ge 0\end{array} \right. \Leftrightarrow ab \ge 0\)
Chọn kết luận đúng: Đồ thị hàm số bậc bốn trùng phương
Đồ thị hàm bậc 4 trùng phương luôn cắt trục tung tại điểm $\left( {0;c} \right)$ chính là cực trị của đồ thị hàm số.
Ngoài ra, đồ thị hàm số bậc 4 trùng phương cũng có thể không cắt $Ox$ nên A sai.
Đồ thị nhận trục tung làm trục đối xứng chứ không phải trục hoành nên C sai.
Đồ thị không có tâm đối xứng nên D sai.
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a > 0} \right)$ có ba cực trị. Nếu ${y_{CT}} > 0$ thì đồ thị hàm số:
Đồ thị hàm số bậc bốn trùng phương có ba cực trị và hệ số $a > 0$ có dạng:
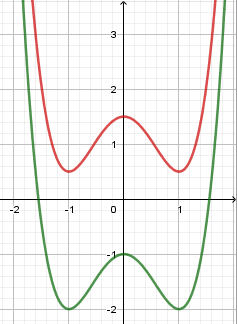
Quan sát đồ thị ta thấy nếu ${y_{CT}} > 0$ thì đồ thị hàm số nằm hoàn toàn phía trên trục hoành
Cho hàm số $y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)$ có $1$ cực trị. Khi đó, nếu đồ thị hàm số nằm hoàn toàn phía trên trục hoành (không có điểm chung với trục hoành) thì:
Hàm số chỉ có 1 cực trị thì $y' = 0$ có 1 nghiệm $ \Leftrightarrow ab \ge 0$, khi đó đồ thị có dạng:
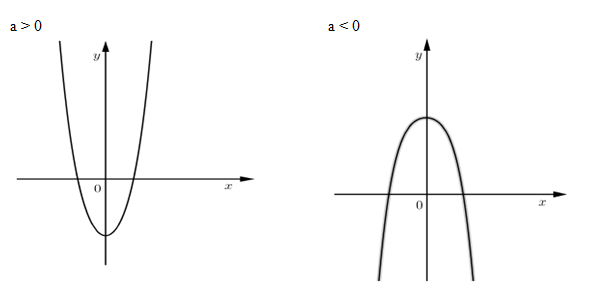
Trong hai trường hợp trên ta thấy nếu đồ thị hàm số nằm hoàn toàn phía trên trục hoành thì chỉ xảy ra trường hợp $a > 0$, do đó $b \ge 0$ và điểm cực tiểu $\left( {0;c} \right)$ cũng phải nằm phía trên trục hoành hay $c > 0$.
Cho hàm số $y = a{x^4} + b{x^2} + c$ có $a < 0,b > 0$. Chọn kết luận sai:
Hàm số $y = a{x^4} + b{x^2} + c$ có $a < 0,b > 0$ nên có $3$ cực trị và đồ thị có dạng như sau:
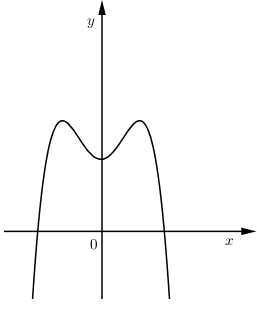
Quan sát đồ thị ta thấy:
- Hàm số có $2$ cực đại và $1$ cực tiểu nên A đúng.
- Đồ thị hàm số nằm hoàn toàn phía dưới trục hoành nếu ${y_{CD}} < 0$ nên B đúng.
- Đồ thị hàm số cắt $Ox$ tại hai điểm phân biệt nếu $c > 0$ nên C đúng, D sai.
Cho hàm số $y = a{x^4} + b{x^2} + c$ có $a > 0,b < 0$. Đồ thị hàm số có $4$ điểm chung với trục hoành nếu:
Hàm số $y = a{x^4} + b{x^2} + c$ có $a > 0,b < 0$ nên có $3$ cực trị và đồ thị của nó có dạng:
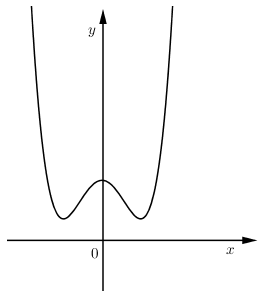
Quan sát đồ thị ta thấy:
- Nếu ${y_{CD}} > 0,{y_{CT}} > 0$ thì đồ thị hàm số không cắt $Ox$ nên điều kiện ${y_{CD}} > 0$ là chưa đủ.
Do đó A sai.
- Nếu ${y_{CT}} < 0,{y_{CD}} < 0$ thì đồ thị hàm số cắt $Ox$ tại 2 điểm phân biệt nên điều kiện ${y_{CT}} < 0$ là chưa đủ.
Do đó B sai.
- Nếu ${y_{CD}}.{y_{CT}} < 0$ thì ${y_{CT}} < 0 < {y_{CD}}$ nên đường thẳng $y = 0$ cắt đồ thị hàm số tại $4$ điểm phân biệt.
Do đó C đúng.
- Nếu ${y_{CD}}.{y_{CT}} > 0$ thì ${y_{CD}} > {y_{CT}} > 0$ hoặc ${y_{CT}} < {y_{CD}} < 0$ nên đồ thị hàm số không thể cắt $Ox$ tại $4$ điểm phân biệt.
Do đó D sai.
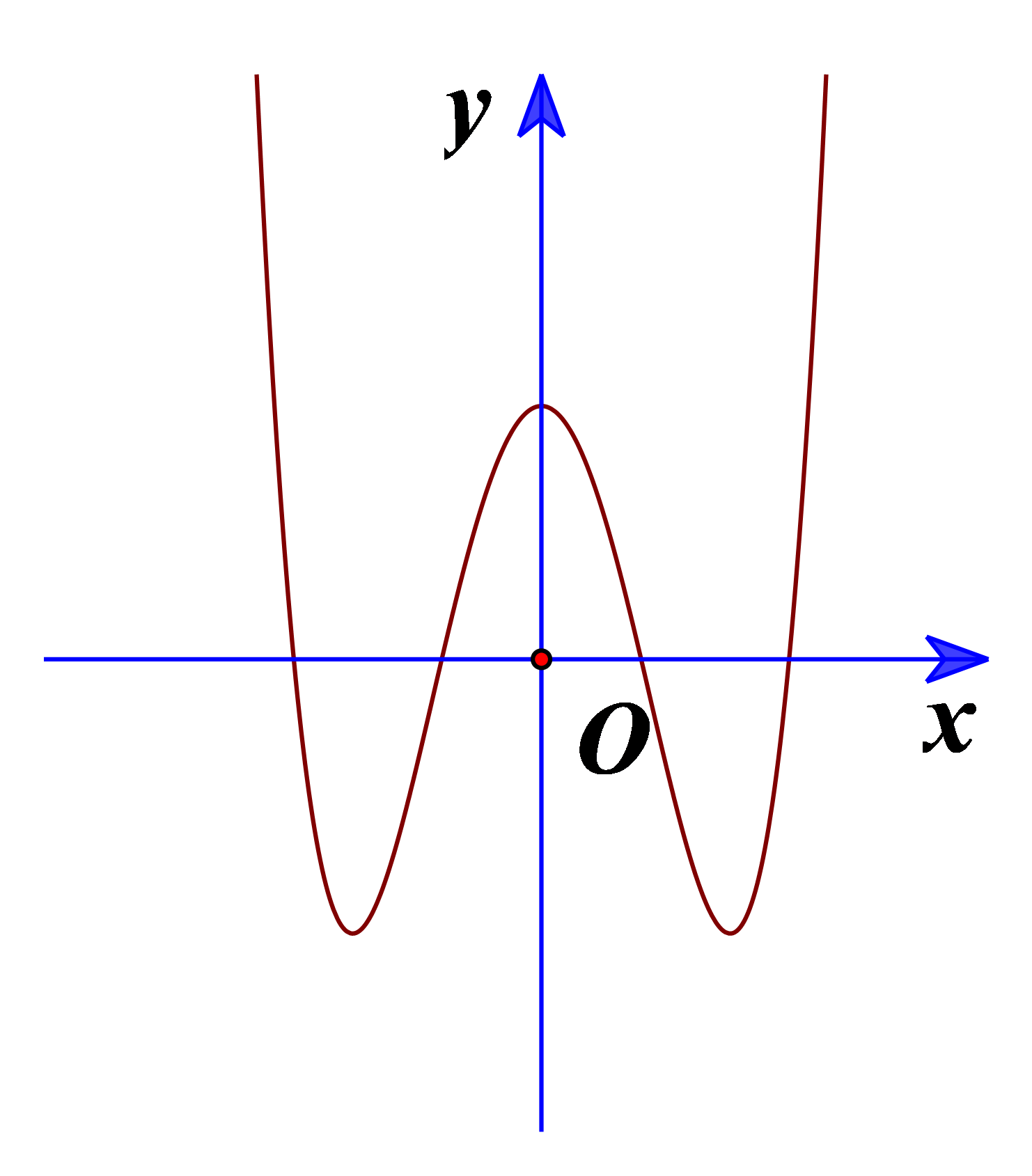
Cho hàm số \(y = (a - 1){x^4} + (b + 2){x^2} + c - 1\) có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây là đúng?
\(a > 1,b < - 2,c > 1\).
\(a > 1,b < - 2,c > 1\).
\(a > 1,b < - 2,c > 1\).
Đồ thị đi lên khi \(x \to + \infty \) nên \(a - 1 > 0 \Leftrightarrow a > 1\).
Đồ thị đi qua điểm \((0;c - 1)\) có tung độ nằm phía trên trục hoành nên \(c - 1 > 0 \Leftrightarrow c > 1\).
Đồ thị hàm số có 3 điểm cực trị nên \((a - 1) \cdot (b + 2) < 0\) mà \(a > 1\) nên \(b + 2 < 0 \Leftrightarrow b < - 2\).
Điểm nào dưới đây thuộc đồ thị của hàm số \(y = {x^4} + {x^2} - 2\) ?
Thay \(M( - 1;0)\) vào đồ thị ta được: \({\left( { - 1} \right)^4} + {\left( { - 1} \right)^2} - 2 = 0\)
Cho hàm số \(y = a{x^4} + b{x^2} + c(a,b,c \in \mathbb{R})\) có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng
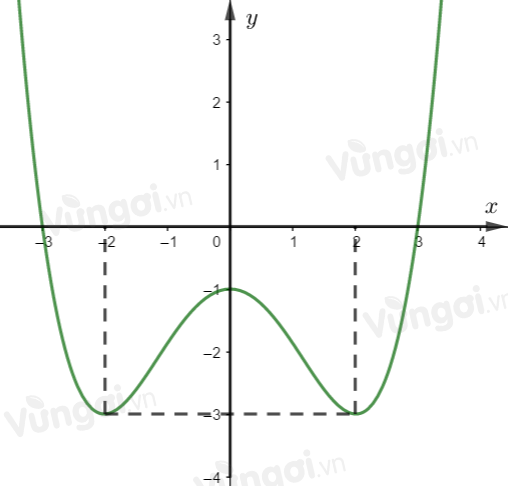
Quan sát đồ thị hàm số, giá trị cực đại của hàm số đã cho bằng \( - 1\)

