Khảo sát sự biến thiên và vẽ đồ thị của hàm phân thức
Kỳ thi ĐGTD ĐH Bách Khoa
Hàm số \(y = \dfrac{{3x - 6}}{{x - 2}}\) xác định khi:
Hàm số xác định khi \(x - 2 \ne 0 \Leftrightarrow x \ne 2\).
Tiệm cận đứng của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) với \(ad - bc \ne 0\) là:
Đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\left( {ad - bc \ne 0} \right)\) có tiệm cận đứng là đường thẳng \(x = - \dfrac{d}{c}\).
Cho hàm số \(y = \dfrac{{x - 3}}{{2x - 6}}\), chọn kết luận đúng:
Ta có: \(y = \dfrac{{x - 3}}{{2x - 6}} = \dfrac{1}{2},\forall x \ne 3\)
Do đó đồ thị hàm số không có tiệm cận đứng.
Giao điểm của hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) được gọi là:
Giao điểm của hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) được gọi là tâm đối xứng của đồ thị hàm số.
Giao điểm hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ - x + 1}}{{2x - 3}}\) là:
Đồ thị hàm số có tiệm cận đứng \(x = \dfrac{3}{2}\) và tiệm cận ngang \(y = - \dfrac{1}{2}\)
Giao điểm hai đường tiệm cận của đồ thị hàm số \(y = \dfrac{{ - x + 1}}{{2x - 3}}\) là \(\left( {\dfrac{3}{2}; - \dfrac{1}{2}} \right)\)
Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có đồ thị như hình bên thì:

Từ đồ thị ta thấy hàm số nghịch biến nên \(ad - bc < 0\).
Hàm số \(y = \dfrac{{ax + b}}{{cx + d}}\) có bảng biến thiên như hình vẽ thì:
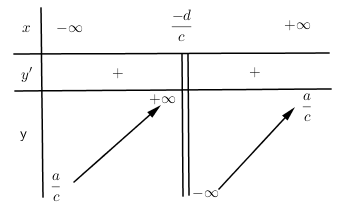
Từ bảng biến thiên ta thấy hàm số đồng biến trên mỗi khoảng \(\left( { - \infty ; - \dfrac{d}{c}} \right)\) và \(\left( { - \dfrac{d}{c}; + \infty } \right)\) nên \(ad - bc > 0\).
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
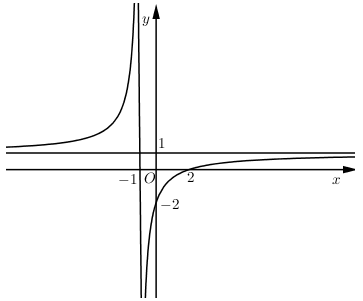
Nhận xét: Đồ thị hàm số có tiệm cận ngang là $y = 1$ và tiệm cận đứng là \(x = - 1\)
Đồ thị hàm số đi qua 2 điểm \(\left( {2;\,0} \right)\) và \(\left( {0;\, - 2} \right)\)
Đáp án C và D không có tiệm cận đứng là \(x = - 1\)
\(\Rightarrow\) Loại đáp án C và D
Xét đáp án A và B đều có tiệm cận đứng là \(x = - 1\) và tiệm cận ngang là $y = 1$
Vì đồ thị hàm số đi qua điểm \(\left( {2;\,0} \right)\)
\(\Rightarrow\) thay $x = 2, y = 0$ vào hàm số thì chỉ có đáp án A thỏa mãn
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
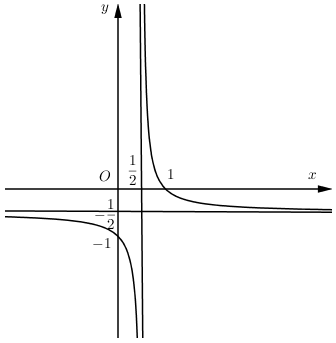
Nhận xét: Đồ thị hàm số có tiệm cận đứng là \(x = \dfrac{1}{2}\) và tiệm cận ngang là \(y = \dfrac{{ - 1}}{2}\)
Nhận thấy các đáp án A, B, C, D đều thỏa mãn tiệm cận đứng là \(x = \dfrac{1}{2}\) và tiệm cận ngang là \(y = \dfrac{{ - 1}}{2}\)
Mặt khác: Đồ thị hàm số đi qua 2 điểm \(\left( {0;\, - 1} \right)\) Þ Thay \(x = 0;\,y = - 1\) vào các hàm số thì chỉ đáp án B thỏa mãn.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên:
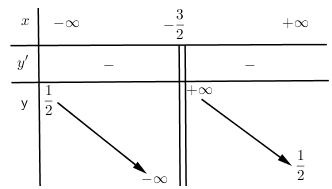
Bảng biến thiên trên là bảng biến thiên của đồ thị hàm số nào?
Nhận xét: Đồ thị hàm số \(y = f\left( x \right)\) có $\left\{ \begin{align}& \xrightarrow{TCD}x=-\dfrac{3}{2} \\ & \xrightarrow{TCN}y=\dfrac{1}{2} \\ \end{align} \right.$
Vậy hàm số đó là \(y = \dfrac{{x + 2}}{{2x + 3}}\).
Hàm số nào dưới đây có thể có bảng biến thiên như hình vẽ?
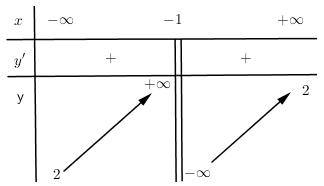
- Tiệm cận đứng \(x = - 1\) nên loại A.
- Tiệm cận ngang \(y = 2\), cả 3 đáp án B, C, D đều thỏa mãn.
- Hàm số đồng biến trên TXĐ nên \(ad - bc > 0\). Thử vào các đáp án chỉ có đáp án C thỏa mãn.
Cho hàm số \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
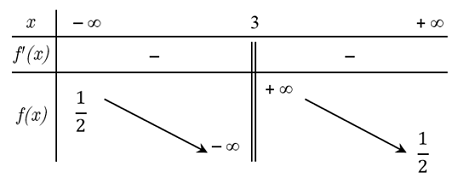
Khẳng định nào dưới đây đúng?
TXĐ: \(D = \mathbb{R}\backslash \left\{ 3 \right\}\).
Dựa vào BBT, ta có: \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to \pm \infty } f\left( x \right) = \dfrac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\\mathop {\lim }\limits_{x \to {3^ + }} f\left( x \right) = + \infty ,\mathop {\lim }\limits_{x \to {3^ - }} f\left( x \right) = - \infty \end{array} \right. \Rightarrow \left\{ \begin{array}{l}\dfrac{a}{b} = \dfrac{1}{2}\\ - \dfrac{c}{b} = 3\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}a = \dfrac{b}{2}\\c = - 3b\end{array} \right.\)
Ta có: \(f\left( x \right) = \dfrac{{ax - 1}}{{bx + c}}\, \Rightarrow f'\left( x \right) = \dfrac{{ac + b}}{{{{\left( {bx + c} \right)}^2}}}\).
Dựa vào BBT ta thấy \(f'\left( x \right) < 0\,\,\,\forall x \ne 3 \Leftrightarrow ac + b < 0\,\,\forall x \ne 3\)\( \Leftrightarrow \dfrac{b}{2}.\left( { - 3b} \right) + b < 0 \Leftrightarrow \left[ \begin{array}{l}b < 0\\b > \dfrac{2}{3}\end{array} \right.\).
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) như hình vẽ bên:
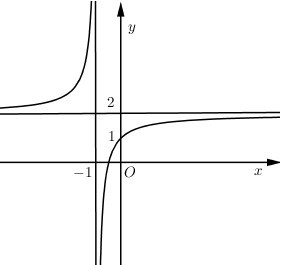
Chọn kết luận đúng:
Đồ thị hàm số \(y = \dfrac{{2x + b}}{{cx + d}}\) có \(\left\{ \begin{align}& \xrightarrow{TCN}y=\dfrac{2}{c}=2\Rightarrow c=1 \\ & \xrightarrow{TCD}x=-\dfrac{d}{c}=-\dfrac{d}{1}=-1\Rightarrow d=1 \\ \end{align} \right.\)
Hàm số có dạng \(y = \dfrac{{2x + b}}{{x + 1}}\left( C \right)\).
Ta có điểm \(\left( {0;1} \right) \in \left( C \right)\).
Thay \(x = 0\) và \(y = 1\) vào hàm số ta được \(1 = \dfrac{{2.0 + b}}{{0 + 1}} \Rightarrow b = 1\) \( \Rightarrow b + c + d = 3\).
Cho hàm số \(y = \dfrac{{3x + 1}}{{x + 2}}\left( C \right).\) Các đường tiệm cận của (C) cùng với 2 trục tọa độ tạo thành hình chữ nhật có diện tích bằng:

Đồ thị hàm số \(y = \dfrac{{3x + 1}}{{x + 2}}\) có:
- Tiệm cận đứng là \(x = - 2\).
- Tiệm cận ngang là \(y = 3\).
Diện tích hình chữ nhật được tạo bởi 2 tiệm cận là: \(S=\left| -2 \right|.\left| 3 \right|=6\) đvdt.
Cho hàm số \(y = \dfrac{{x + b}}{{cx - 1}}\) có đồ thị như hình bên. Mệnh đề nào dưới đây đúng?

Đồ thị hàm số \(y = \dfrac{{x + b}}{{cx - 1}}\) có TCĐ: \(x = \dfrac{1}{c} > 0 \Rightarrow c > 0.\)
Đồ thị hàm số \(y = \dfrac{{x + b}}{{cx - 1}}\) cắt trục tung tại điểm có tung độ \(y = - b < 0 \Rightarrow b > 0.\)
Cho hàm số \(y = f\left( x \right) = \frac{{ax + b}}{{cx + d}}\) với \(a,\,\,b,\,\,c,\,\,d \in \mathbb{R}\), \(c \ne 0\) có đồ thị \(y = f'\left( x \right)\) như hình vẽ bên. Biết rằng giá trị nhỏ nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ {1;2} \right]\) bằng \(3\). Giá trị của \(f\left( { - 2} \right)\) bằng:
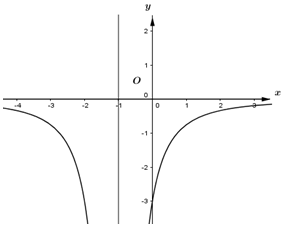
Dựa vào đồ thị hàm số ta thấy \(f'\left( x \right) < 0\,\,\forall x \in \mathbb{R}\backslash \left\{ { - 1} \right\}\), do đó \(f'\left( x \right) < 0\,\,\forall x \in \left( {1;2} \right)\).
\( \Rightarrow \) Hàm số \(y = f\left( x \right)\) nghịch biến trên \(\left( {1;2} \right)\) \( \Rightarrow \mathop {\min }\limits_{\left[ {1;2} \right]} f\left( x \right) = f\left( 2 \right)\)\( \Rightarrow \frac{{2a + b}}{{2c + d}} = 3\).
Ta có: \(f'\left( x \right) = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}\) có TXĐ \(D = \mathbb{R}\backslash \left\{ { - 1} \right\} \Rightarrow \) \( - c + d = 0 \Leftrightarrow c = d\).
Đồ thị hàm số \(y = f'\left( x \right)\) đi qua điểm \(\left( {0; - 3} \right)\) \( \Rightarrow \frac{{ad - bc}}{{{d^2}}} = - 3\).
\( \Rightarrow \frac{{ad - bd}}{{{d^2}}} = - 3 \Leftrightarrow a - b = - 3d = - 3c\).
Lại có \(\frac{{2a + b}}{{2c + d}} = 3 \Leftrightarrow \frac{{2a + b}}{{2c + c}} = 3\) \( \Leftrightarrow 2a + b = 9c\).
Ta có: \(\left\{ \begin{array}{l}a - b = - 3c\\2a + b = 9c\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2c\\b = 5c\end{array} \right.\)\( \Rightarrow y = \frac{{2cx + 5c}}{{cx + c}}\).
Vậy \(y\left( { - 2} \right) = \frac{{ - 4c + 5c}}{{ - 2c + c}} = - 1\).

