Tích phân

Các mệnh đề A, B, C đều đúng. Mệnh đề D sai.

Ta có $\int\limits_{ - 1}^a {{e^{x + 1}}dx}  = \left. {{e^{x + 1}}} \right|_{ - 1}^a = {e^{a + 1}} - 1$.

Vậy yêu cầu bài toán trở thành ${e^{a + 1}} - 1 = {e^2} - 1{\rm{  }}\Leftrightarrow a+1=2 \Leftrightarrow {\rm{  }}a = 1$.

Dễ thấy các công thức a) đúng vì tích phân có hai cận bằng nhau thì có giá trị $0$.

Công thức c) là đúng theo tính chất tích phân.

Công thức b) sai vì $\int\limits_a^b {f\left( x \right)dx}  =  - \int\limits_b^a {f\left( x \right)dx}$

Tính tích phân cho từng hàm số trong các đáp án:

+) $\int\limits_0^\pi  {\cos 3xdx}  = \left. {\dfrac{1}{3}\sin 3x} \right|_0^\pi  = 0$,

+) $\int\limits_0^\pi  {\sin 3xdx}  =  - \left. {\dfrac{1}{3}\cos 3x} \right|_0^\pi  = \dfrac{2}{3}$,

+) $\int\limits_0^\pi  {\cos \left( {\dfrac{x}{4} + \dfrac{\pi }{2}} \right)dx}  = \left. {4\sin \left( {\dfrac{x}{4} + \dfrac{\pi }{2}} \right)} \right|_0^\pi  = 2\left( {\sqrt 2  - 2} \right)$,

+) $\int\limits_0^\pi  {\sin \left( {\dfrac{x}{4} + \dfrac{\pi }{2}} \right)dx}  = \left. { - 4\cos \left( {\dfrac{x}{4} + \dfrac{\pi }{2}} \right)} \right|_0^\pi  = 2\sqrt 2$.

Vậy chọn $f(x) = \cos 3x$.

$I = \int\limits_1^4 {f'(x)dx}  = f\left. {(x)} \right|_1^4 = f(4) - f(1) = 10 - 2 = 8$

Ta có $\int\limits_0^1 {\left[ {3 - 2f\left( x \right)} \right]{\rm{d}}x}  = \int\limits_0^1 {{\rm{3d}}x}  - 2\int\limits_0^1 {f\left( x \right){\rm{d}}x}  = \left. {3x} \right|_0^1 - 2\int\limits_0^1 {f\left( x \right){\rm{d}}x}  = 3 - 2\int\limits_0^1 {f\left( x \right){\rm{d}}x}$

Mặt khác $\int\limits_0^1 {\left[ {3 - 2f\left( x \right)} \right]{\rm{d}}x}  = 5 \Rightarrow 3 - 2\,\int\limits_0^1 {f\left( x \right){\rm{d}}x}  = 5 \Leftrightarrow \int\limits_0^1 {f\left( x \right){\rm{d}}x}  =  - \,1.$

Cách 1:

$\begin{array}{l}I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\dfrac{{dx}}{{\sin x}}} \\= \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\dfrac{{\left( {{{\cos }^2}\dfrac{x}{2} + {{\sin }^2}\dfrac{x}{2}} \right)}}{{2\sin \dfrac{x}{2}\cos \dfrac{x}{2}}}dx} \\ = \dfrac{1}{2}\int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\left( {\cot \dfrac{x}{2} + \tan \dfrac{x}{2}} \right)dx} \\ = \left. {\left[ {\ln \left| {\sin \dfrac{x}{2}} \right| - \ln \left| {\cos \dfrac{x}{2}} \right|} \right]} \right|_{\frac{\pi }{3}}^{\frac{\pi }{2}}\\ = \left[ {\ln \dfrac{{\sqrt 2 }}{2} - \ln \dfrac{{\sqrt 2 }}{2}} \right] - \left[ {\ln \dfrac{1}{2} - \ln \dfrac{{\sqrt 3 }}{2}} \right]\\ = \ln \sqrt 3 .\end{array}$

Cách 2:

Bước 1: Dùng máy tính như hình dưới, thu được giá trị $0,549306...$

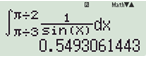
Bước 2: Lấy ${e^{0,549306...}}$ cho kết quả $1,732050808... \approx \sqrt 3$. Chọn $\dfrac{1}{2}\ln 3$.

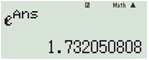
Cách 3:

Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng $0$ thì ngưng)

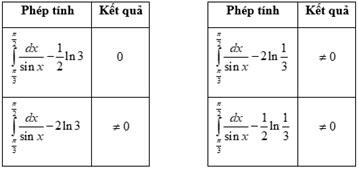
Chọn $\dfrac{1}{2}\ln 3$.

Ta có: $F\left( x \right) = \int\limits_1^x {\left( {t + 1} \right)dt}  = \left. {\left( {\dfrac{{{t^2}}}{2} + t} \right)} \right|_1^x = \dfrac{{{x^2}}}{2} + x - \dfrac{1}{2} - 1 = \dfrac{{{x^2}}}{2} + x - \dfrac{3}{2}$

Hàm số $y = F\left( x \right)$ là hàm số bậc hai, hệ số $a > 0$ nên nó đạt GTNN tại $x =  -1 \in \left[ { - 1;1} \right]$.

Khi đó $F(-1)=\dfrac{1}{2}+(-1)-\dfrac{3}{2}=-2$

$K = \int\limits_{ - 2}^0 {\left( {4 - {e^{-\frac{x}{2}}}} \right)dx}  + 2e = \left. {\left( {4x + 2{e^{-\frac{x}{2}}}} \right)} \right|_{ - 2}^0 + 2e = 2 - \left( { - 8 + 2e} \right) + 2e = 10$

Vì $f\left( x \right) = {x^2} \ge 0,\forall x \in \left[ {0;1} \right]$ nên $\int\limits_0^1 {f\left( x \right)dx}  \ge 0$. Do đó A đúng, D sai.

Vì $g\left( x \right) = {x^3} \ge 0,\forall x \in \left[ {0;1} \right]$ nên $\int\limits_0^1 {g\left( x \right)dx}  \ge 0$. Do đó B sai.

Vì ${x^2} \ge {x^3}$ trên $\left[ {0;1} \right]$ nên $\int\limits_0^1 {f\left( x \right)dx}  \ge \int\limits_0^1 {g\left( x \right)dx}$. Do đó C sai.

$\int\limits_0^1 {\dfrac{1}{{{x^2} - x - 2}}dx}  = \int\limits_0^1 {\dfrac{1}{{(x - 2)(x + 1)}}dx}  = \dfrac{1}{3}\int\limits_0^1 {\left[ {\dfrac{1}{{x - 2}} - \dfrac{1}{{x + 1}}} \right]dx}  = \dfrac{1}{3}\left. {\left[ {\ln \left| {x - 2} \right| - \ln \left| {x + 1} \right|} \right]} \right|_0^1 =  - \dfrac{{2\ln 2}}{3}$

Dựa vào các đáp án ta có nhận xét sau:

$\int\limits_a^c {f(x)dx = } \int\limits_a^b {f(x)dx}  + \int\limits_b^c {f(x)dx}$ => A đúng

$\int\limits_a^b {f(x)dx = } \int\limits_a^c {f(x)dx}  - \int\limits_b^c {f(x)dx}$ B đúng

$\int\limits_a^b {f(x)dx = } \int\limits_b^a {f(x)dx}  + \int\limits_a^c {f(x)dx}$ C sai

$\int\limits_a^b {cf(x)dx =  - c} \int\limits_b^a {f(x)dx}$  D đúng.

Ta có: $\int\limits_1^4 {f'\left( x \right)dx}  = 17 \Rightarrow \left. {f\left( x \right)} \right|_1^4 = 17 \Rightarrow f\left( 4 \right) - f\left( 1 \right) = 17 \Rightarrow f\left( 4 \right) - 12 = 17 \Rightarrow f\left( 4 \right) = 29$

Ta có: $I = \int\limits_1^2 {{x^5}} dx = \left. {\dfrac{{{x^6}}}{6}} \right|_1^2 = \dfrac{{21}}{2}$.

Ta có:

$\int\limits_5^2 {\left[ {2 - 4f\left( x \right)} \right]dx}  = \int\limits_5^2 {2dx}  - 4\int\limits_5^2 {f\left( x \right)dx}  = \left. {2x} \right|_5^2 + 4\int\limits_2^5 {f\left( x \right)dx}  = 2.2 - 2.5 + 4.10 = 34$

Ta có:

$\begin{array}{l}\int\limits_a^d {f\left( x \right)dx}  = \int\limits_a^c {f\left( x \right)dx}  + \int\limits_c^b {f\left( x \right)dx}  + \int\limits_b^d {f\left( x \right)dx} \\ \Rightarrow \int\limits_c^b {f\left( x \right)dx}  = \int\limits_a^d {f\left( x \right)dx}  - \int\limits_a^c {f\left( x \right)dx}  - \int\limits_b^d {f\left( x \right)dx} \\ \Rightarrow \int\limits_c^b {f\left( x \right)dx}  = 10 - 7 - 18 =  - 15 \Rightarrow \int\limits_b^c {f\left( x \right)dx}  = 15\end{array}$

$I = \int\limits_0^2 {{x^3}dx}  = \left. {\dfrac{{{x^4}}}{4}} \right|_0^2 = 4$ và $J = \int\limits_0^2 {xdx}  = \left. {\dfrac{{{x^2}}}{2}} \right|_0^2 = 2$.

Suy ra $I.J = 8$.

Ta có: $\int\limits_1^4 {\left[ {f\left( x \right) + g\left( x \right)} \right]dx}  = \int\limits_1^4 {f\left( x \right)dx}  + \int\limits_1^4 {f\left( x \right)dx}  = 10$ nên A đúng.

$\int\limits_1^4 {f\left( x \right)dx}  = \int\limits_1^3 {f\left( x \right)dx}  + \int\limits_3^4 {f\left( x \right)dx}  \Rightarrow \int\limits_3^4 {f\left( x \right)dx}  = \int\limits_1^4 {f\left( x \right)dx}  - \int\limits_1^3 {f\left( x \right)dx}  = 3 - \left( { - 2} \right) = 5$ nên C đúng, B sai.

$\int\limits_1^4 {\left[ {4f\left( x \right) - 2g\left( x \right)} \right]dx}  = 4\int\limits_1^4 {f\left( x \right)dx}  - 2\int\limits_1^4 {g\left( x \right)dx}  =  - 2$ nên D đúng.

Ta có: $\int\limits_0^1 {\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]dx = 5}$

$\begin{array}{l}\int\limits_0^1 {{{\left[ {f\left( x \right) + 1} \right]}^2}dx = 36}  \Leftrightarrow \int\limits_0^1 {\left[ {{f^2}\left( x \right) + 2f\left( x \right) + 1} \right]} dx = 36\\ \Rightarrow \int\limits_0^1 {\left[ {{f^2}\left( x \right) + 2f\left( x \right) + 1} \right]} dx - \int\limits_0^1 {\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]dx}  = 36 - 5\\ \Leftrightarrow \int\limits_0^1 {\left[ {3f\left( x \right) + 1} \right]dx}  = 31 \Leftrightarrow 3\int\limits_0^1 {f\left( x \right)dx}  + \int\limits_0^1 {dx}  = 31\\ \Leftrightarrow 3\int\limits_0^1 {f\left( x \right)dx}  + \left. x \right|_0^1 = 31 \Leftrightarrow 3\int\limits_0^1 {f\left( x \right)dx}  + 1 = 31\\ \Leftrightarrow 3\int\limits_0^1 {f\left( x \right)dx}  = 30 \Leftrightarrow \int\limits_0^1 {f\left( x \right)dx}  = 10.\end{array}$

Phương pháp tự luận

$\begin{array}{c}I = \int\limits_0^{2\pi } {\sqrt {{{\left( {\sin \dfrac{x}{2} + \cos \dfrac{x}{2}} \right)}^2}} } dx = \int\limits_0^{2\pi } {\left| {\sin \dfrac{x}{2} + \cos \dfrac{x}{2}} \right|} dx = \sqrt 2 \int\limits_0^{2\pi } {\left| {\sin \left( {\dfrac{x}{2} + \dfrac{\pi }{4}} \right)} \right|} dx\\ = \sqrt 2 \left[ {\int\limits_0^{\dfrac{{3\pi }}{2}} {\sin \left( {\dfrac{x}{2} + \dfrac{\pi }{4}} \right)} dx - \int\limits_{\dfrac{{3\pi }}{2}}^{2\pi } {\sin \left( {\dfrac{x}{2} + \dfrac{\pi }{4}} \right)dx} } \right] = 4\sqrt 2 \end{array}$