Câu hỏi:
2 năm trước
Tích phân \(I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\dfrac{{dx}}{{\sin x}}} \) có giá trị bằng
Trả lời bởi giáo viên
Đáp án đúng: c
Cách 1:
\(\begin{array}{l}I = \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\dfrac{{dx}}{{\sin x}}} \\= \int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\dfrac{{\left( {{{\cos }^2}\dfrac{x}{2} + {{\sin }^2}\dfrac{x}{2}} \right)}}{{2\sin \dfrac{x}{2}\cos \dfrac{x}{2}}}dx} \\ = \dfrac{1}{2}\int\limits_{\frac{\pi }{3}}^{\frac{\pi }{2}} {\left( {\cot \dfrac{x}{2} + \tan \dfrac{x}{2}} \right)dx} \\ = \left. {\left[ {\ln \left| {\sin \dfrac{x}{2}} \right| - \ln \left| {\cos \dfrac{x}{2}} \right|} \right]} \right|_{\frac{\pi }{3}}^{\frac{\pi }{2}}\\ = \left[ {\ln \dfrac{{\sqrt 2 }}{2} - \ln \dfrac{{\sqrt 2 }}{2}} \right] - \left[ {\ln \dfrac{1}{2} - \ln \dfrac{{\sqrt 3 }}{2}} \right]\\ = \ln \sqrt 3 .\end{array}\)
Cách 2:
Bước 1: Dùng máy tính như hình dưới, thu được giá trị \(0,549306...\)
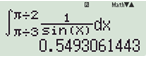
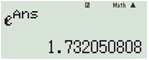
Bước 2: Lấy \({e^{0,549306...}}\) cho kết quả \(1,732050808... \approx \sqrt 3 \). Chọn \(\dfrac{1}{2}\ln 3\).
Cách 3:
Thực hiện các phép tính sau trên máy tính (đến khi thu được kết quả bằng \(0\) thì ngưng)
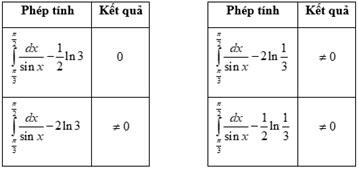
Chọn \(\dfrac{1}{2}\ln 3\).
Hướng dẫn giải:
Viết lại tử số \(1 = {\sin ^2}\dfrac{x}{2} + {\cos ^2}\dfrac{x}{2}\) và mẫu số \(\sin x = 2\sin \dfrac{x}{2}\cos \dfrac{x}{2}\) rồi tính tích phân, sử dụng công thức nguyên hàm hàm lượng giác.
