Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S)$ có tâm $I(2;1;-1)$ và tiếp xúc với mặt phẳng \((\alpha )\) có phương trình \(2x - 2y - z + 3 = 0\). Bán kính của $(S)$ là:
Vì $(S)$ tiếp xúc với mặt phẳng \((\alpha )\) nên ta có \(R = d(I,\alpha )\).
Suy ra \(R = d(I,\alpha ) = \dfrac{{\left| {2.2 - 2.1 - ( - 1) + 3} \right|}}{{\sqrt {4 + 4 + 1} }} = \dfrac{6}{3} = 2\)
Trong không gian với hệ tọa độ $Oxyz$ cho mặt cầu $(S):{(x - 1)^2} + {(y + 1)^2} + {(z + 2)^2} = 4$ và 2 đường thẳng ${\Delta _1}:\left\{ \begin{array}{l}x = 2t\\y = 1 - t\\z = t\end{array} \right.$ và ${\Delta _2}:\dfrac{{x - 1}}{{ - 1}} = \dfrac{y}{1} = \dfrac{z}{{ - 1}}$. Một phương trình mặt phẳng $(P)$ song song với ${\Delta _1},{\Delta _2}$ và tiếp xúc với mặt cầu $(S)$ là:
$(S)$ có tâm $I(1; - 1; - 2);R = 2$
Vì $(P)$ song song với ${\Delta _1},{\Delta _2}$ có vtcp tương ứng là \(\overrightarrow {{u_1}} = \left( {2; - 1;1} \right);\overrightarrow {{u_2}} = \left( { - 1;1; - 1} \right)\) ta có $\overrightarrow {{n_P}} = {\rm{[}}\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} {\rm{]}} = \left( {\left| {\begin{array}{*{20}{c}}{ - 1}&1\\1&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}1&2\\{ - 1}&{ - 1}\end{array}} \right|;\left| {\begin{array}{*{20}{c}}2&{ - 1}\\{ - 1}&1\end{array}} \right|} \right) = (0;1;1)$
Gọi $(P):y + z + d = 0$
$\begin{array}{l}d(I;P) = \dfrac{{\left| { - 1 - 2 + d} \right|}}{{\sqrt 2 }} = \dfrac{{\left| {d - 3} \right|}}{{\sqrt 2 }}\\ \Rightarrow \dfrac{{\left| {d - 3} \right|}}{{\sqrt 2 }} = 2 \Leftrightarrow \left[ \begin{array}{l}d - 3 = 2\sqrt 2 \\d - 3 = - 2\sqrt 2 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}d = 3 + 2\sqrt 2 \\d = 3 - 2\sqrt 2 \end{array} \right. \Rightarrow \left[ \begin{array}{l}y + z + 3 + 2\sqrt 2 = 0\\y + z + 3 - 2\sqrt 2 = 0\end{array} \right.\end{array}$
Trong không gian với hệ tọa độ $Oxyz$, cho hai điểm $A\left( {0; - 1;0} \right),B\left( {1;1; - 1} \right)$ và mặt cầu $(S):{x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 3 = 0$. Mặt phẳng $(P)$ đi qua $A, B$ và cắt mặt cầu $(S)$ theo giao tuyến là đường tròn có bán kính lớn nhất có phương trình là:
$(S):{x^2} + {y^2} + {z^2} - 2x + 4y - 2z - 3 = 0$ có tâm $I(1;-2;1)$ và bán kính $R = 3$.
Do $(P)$ đi qua $A, B$ và cắt $(S)$ theo giao tuyến là đường tròn có bán kính lớn nhất nên $(P)$ đi qua tâm $I$ của $(S)$
Ta có: $\overrightarrow {IA} = \left( { - 1;1; - 1} \right),\overrightarrow {IB} = \left( {0;3; - 2} \right)$; $\overrightarrow {{n_{(P)}}} = \left[ {\overrightarrow {IA} ,\overrightarrow {IB} } \right] = \left( {1; - 2; - 3} \right)$
Phương trình mặt phẳng $(P): 1(x – 0) – 2(y + 1) – 3(z – 0) = 0$ hay $x – 2y – 3z – 2 = 0$.
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S)$ đi qua điểm \(A(2; - 2;5)\) và tiếp xúc với các mặt phẳng \(\left( \alpha \right):x = 1,\left( \beta \right):y = - 1,\left( \gamma \right):z = 1\). Bán kính của mặt cầu $(S)$ bằng:
Gọi $I\left( {a;b;c} \right)$. Do mặt cầu tiếp xúc với các mặt phẳng \((\alpha),\left( \beta \right),\left( \gamma \right)\) nên ta có ${\rm{d}}\left( {I,\left( \alpha \right)} \right) = {\rm{d}}\left( {I,\left( \beta \right)} \right) = {\rm{d}}\left( {I,\left( \gamma \right)} \right) = R$
Suy ra $\left| {a - 1} \right| = \left| {b + 1} \right| = \left| {c - 1} \right| = R$
Do điểm $A\left( {2; - 2;5} \right)$ thuộc miền ${\rm{x}} > 1;y < - 1;z > 1$ nên $I\left( {a;b;c} \right)$ cũng thuộc miền ${\rm{x}} > 1;y < - 1;z > 1$
Khi đó $I\left( {R + 1; - 1 - R;R + 1} \right)$. Mặt khác $IA = R \Rightarrow {\left( {R - 1} \right)^2} + {\left( {R - 1} \right)^2} + {\left( {R - 4} \right)^2} = {R^2} \Leftrightarrow R = 3$
Trong không gian với hệ tọa độ $Oxyz$, cho mặt cầu $(S):{(x - 2)^2} + {(y + 1)^2} + {(z - 4)^2} = 10$ và mặt phẳng $(P): - 2x + y + \sqrt 5 z + 9 = 0$ . Gọi $(Q)$ là tiếp diện của $(S)$ tại $M(5;0;4)$ . Tính góc giữa $(P)$ và $(Q)$.
Gọi mặt cầu tâm $I(2;-1;4)$.
Mặt phẳng tiếp diện của mặt cầu $(S)$ (tâm $I$, bán kính $R$) tại điểm $M$ chính là mặt phẳng đi qua điểm $M$ và vuông góc với bán kính $IM $ tại tiếp điểm $M$
Mặt phẳng qua $M(5;0;4)$ vuông góc với $IM $ ($\overrightarrow {IM} = (3;1;0)$) có phương trình:
\((Q): 3\left( {x - 5} \right) + {\text{ }}y\; = 0 \Leftrightarrow 3x + y-15 = 0\)
Có: ${\overrightarrow n _P}( - 2;1;\sqrt 5 );{\overrightarrow n _Q}(3;1;0)$
Nên ta có:
\(\cos \widehat {\left( {(P);(Q)} \right)} = \left| {\cos \widehat {\left( {\overrightarrow {{n_P}} ;\overrightarrow {{n_Q}} } \right)}} \right| = \dfrac{{\left| { - 6 + 1} \right|}}{{\sqrt {10} .\sqrt {10} }} = \dfrac{1}{2} \Rightarrow \widehat {\left( {(P);(Q)} \right)} = {60^0}\)
Trong không gian $Oxyz $, xác định tọa độ tâm $I$ của đường tròn giao tuyến của mặt cầu \((S) :{\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 1} \right)^2} = 64\) với mặt phẳng\(\left( \alpha \right):2x + 2y + z + 10 = 0.\)
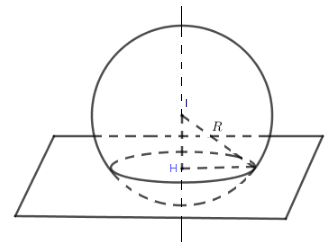
$(S)$ có tâm $I(1;1;1)$ và bán kính $R=8$.
Tâm đường tròn giao tuyến $(C)$ là hình chiếu vuông góc $H$ của $I$ trên $(P)$.
Đường thẳng $\Delta $ qua $I$ và vuông góc với $(P)$ có phương trình là $\dfrac{{x - 1}}{2} = \dfrac{{y - 1}}{2} = \dfrac{{z - 1}}{1}$ .
Do $H∈∆$ nên $H(2t+1;2t+1;t+1)$
Ta có $H∈(P)$ nên:
$2(2t+1)+2(2t+1)+t+1+10=0 \Leftrightarrow 9t+15=0 \Leftrightarrow t= - \dfrac{5}{3}$
$ \Rightarrow $ $H( \dfrac{{ - 7}}{3};\dfrac{{ - 7}}{3};\dfrac{{ - 2}}{3})$.
Mặt phẳng $\left( {Oyz} \right)$ cắt mặt cầu $\left( S \right):{x^2} + {y^2} + {z^2} + 2x - 2y + 4z - 3 = 0$ theo một đường tròn có tọa độ tâm là
Phương trình mặt phẳng $(Oyz):x = 0$ nên ta loại được đáp án A.
Véc tơ pháp tuyến của \(\left( {Oyz} \right):\overrightarrow n = (1;0;0)\)
Tọa độ của mặt cầu $(S)$ là $I\left( { - 1;1; - 2} \right)$
Gọi điểm $O$ là điểm cần tìm có $O\left( {0;b;c} \right)$
Do $IO$ vuông góc với $(Oyz)$ nên \(\overrightarrow {OI} \) cùng phương với \(\overrightarrow n = (1;0;0)\)
Suy ra $b = 1;c = - 2$
Viết phương trình mặt cầu có tâm $I\left( { - 1;2;3} \right)$ và tiếp xúc với mặt phẳng $\left( P \right):2x - y - 2z + 1 = 0$
Khoảng cách từ $I$ đến $\left( P \right)$ được tính theo công thức $d\left( {I;\left( P \right)} \right) = \dfrac{{\left| {2.\left( { - 1} \right) - 2 - 2.3 + 1} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} }} = 3$
Phương trình mặt cầu cần tìm là ${\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 9$
Trong không gian với hệ tọa độ $Oxyz$, xét mặt cầu $\left( S \right)$ đi qua hai điểm $A\left( {1;2;1} \right);B\left( {3;2;3} \right)$, có tâm thuộc mặt phẳng $\left( P \right):x - y - 3 = 0$ , đồng thời có bán kính nhỏ nhất, hãy tính bán kính $R$ của mặt cầu $\left( S \right)$?
Gọi $I$ là tâm mặt cầu $\left( S \right),I\left( {a,b,c} \right)$ .
Suy ra \(a - b - 3 = 0 \Rightarrow a = b + 3 \Rightarrow I(b + 3;b;c)\)
\(I{A^2} = I{B^2} = {R^2}\) \( \Leftrightarrow {(b + 2)^2} + {(b - 2)^2} + {(c - 1)^2} = {b^2} + {(b - 2)^2} + {(c - 3)^2}\)
\(\begin{array}{l}
\Leftrightarrow {\left( {b + 2} \right)^2} + {\left( {c - 1} \right)^2} = {b^2} + {\left( {c - 3} \right)^2}\\
\Leftrightarrow {b^2} + 4b + 4 + {c^2} - 2c + 1 = {b^2} + {c^2} - 6c + 9\\
\Leftrightarrow 4b + 4c - 4 = 0\\
\Leftrightarrow b + c - 1 = 0 \Leftrightarrow c = 1 - b
\end{array}\)
\({R^2} = {\left( {b + 2} \right)^2} + {\left( {b - 2} \right)^2} + {\left( { - b} \right)^2} = 3{b^2} + 8 \ge 8 \Rightarrow R \ge 2\sqrt 2 \)
\(\min R = 2\sqrt 2 \) khi $b = 0$
Trong không gian với hệ tọa độ \(Oxyz,\left( \alpha \right)\) cắt mặt cầu $\left( S \right)$ tâm \(I\left( {1; - 3;3} \right)\) theo giao tuyến là đường tròn tâm \(H\left( {2;0;1} \right)\) , bán kính $r = 2$ . Phương trình (S) là:
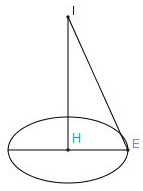
Gọi $E $ là một điểm thuộc đường tròn.
Ta có \(IH = d\left( {I,(\alpha)} \right);\,R = IE;\,r=HE\)
\(IH = \sqrt {1 + {3^2} + {(-2)^2}} = \sqrt {14} \)
Tam giác $IHE$ vuông tại $H$ nên \(IE = \sqrt {I{H^2} + H{E^2}} = \sqrt {14 + 4} = \sqrt {18} \)
Suy ra phương trình mặt cầu $(S)$ là:
\({\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 3} \right)^2} = 18\).
Trong không gian với hệ tọa độ $Oxyz$ , phương trình nào dưới đây là phương trình mặt cầu tâm \(I\left( { - 3;2; - 4} \right)\) và tiếp xúc với mặt phẳng \(\left( {Oxz} \right)\)?
Vì mặt cầu có tâm \(I( - 3;2; - 4)\) tiếp xúc với $mp\left( {Oxz} \right)$ nên $r = 2$.
Phương trình mặt cầu cần tìm là : \({\left( {x + 3} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 4} \right)^2} = 4\).
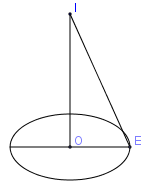
Mặt cầu $\left( S \right)$ có tâm \(I( - 1;2; - 5)\) cắt mặt phẳng \(\left( P \right):2x - 2y - z + 10 = 0\) theo thiết diện là hình tròn có diện tích \(3\pi \). Phương trình của $\left( S \right)$ là:
Gọi $O$ là tâm của đường tròn thiết diện, $E$ là một điểm thuộc đường tròn.
Ta có: $IO = d\left( {I,(P)} \right);R = IE$
\(IO = d\left( {I,(P)} \right) = \dfrac{{|2.( - 1) - 2.2 + 5 + 10|}}{{\sqrt {{2^2} + {2^2} + 1} }} = 3\)
\(S = 3\pi = \pi .O{E^2} \Leftrightarrow O{E^2} = 3\)
Tam giác $IOE$ vuông tại $O$ nên \({R^2} = I{E^2} = I{O^2} + O{E^2} = 3 + 9 = 12.\)
Suy ra phương trình mặt cầu $\left( S \right)$ là:
\({\left( {x + 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z + 5} \right)^2} = 12\) hay \({x^2} + {y^2} + {z^2} + 2x - 4y + 10z + 18 = 0\)
Trong không gian vớ hệ tọa độ $Oxyz$, cho mặt cầu $(S)$ có tâm $I(3;2; - 1)$ và đi qua điểm $A(2;1;2)$. Mặt phẳng nào dưới đây tiếp xúc với $(S)$ tại $A$?
\(\left( P \right)\) là mặt phẳng tiếp xúc với \(\left( S \right)\) tại \(A\) nếu và chỉ nếu \(\left( P \right)\) đi qua \(A\) và $\overrightarrow {IA} \bot \left( P \right)$.
Ta có: \(\overrightarrow {IA} = ( - 1; - 1;3)\) là vec tơ pháp tuyến của mặt phẳng $\left( P \right)$.
Mà $\left( P \right)$ lại đi qua $A\left( {2;1;2} \right)$ nên:
\(\left( P \right): - 1\left( {x - 2} \right) - 1\left( {y - 1} \right) + 3\left( {z - 2} \right) = 0 \Leftrightarrow x + y - 3z + 3 = 0\)
Trong không gian với hệ tọa độ \(Oxyz\) cho mặt phẳng \(\left( P \right):x - 2y + 2z - 3 = 0\) và mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 2x - 4y - 2z + 5 = 0\). Giả sử \(M \in \left( P \right)\) và \(N \in \left( S \right)\) sao cho \(\overrightarrow {MN} \) cùng phương với vectơ \(\overrightarrow u = \left( {1;0;1} \right)\) và khoảng cách \(MN\) lớn nhất. Tính \(MN\)
$(S)$ có tâm $I(–1;2;1)$ và $R = 1$.
Gọi $\overrightarrow v \left( {t;0;t} \right)$là vectơ cùng phương với vectơ $\overrightarrow u \left( {1;0;1} \right)$ sao cho phép tịnh tiến vectơ đó biến $(S)$ thành $(S’)$ tiếp xúc với $(P)$
Phép tịnh tiến vectơ $\overrightarrow v \left( {t;0;t} \right)$ biến $I$ thành $I’ (–1 + t; 2; 1 + t)$
Suy ra $(S’)$ có tâm $I’$ và bán kính $R’ = R = 1$.
$(S’)$ tiếp xúc $(P)$ $ ⇔ d(I; (P)) = 1 \Leftrightarrow \dfrac{{\left| { - 1 + t - 2.2 + 2\left( {1 + t} \right) - 3} \right|}}{{\sqrt {1 + 4 + 4} }} = 1 \Leftrightarrow \left| {3t - 6} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}t = 3\\t = 1\end{array} \right.$
Với $t = 3 \Rightarrow \overrightarrow v \left( {3;0;3} \right) \Rightarrow \left| {\overrightarrow v } \right| = 3\sqrt 2 $
Với $t = 1 ⇒ \overrightarrow v \left( {1;0;1} \right) \Rightarrow \left| {\overrightarrow v } \right| = \sqrt 2 $
Vậy giá trị lớn nhất của $MN $ là $3\sqrt 2 $
Trong không gian với hệ tọa độ $Oxyz $, cho mặt cầu \((S) : {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 9\) và mặt phẳng \((P) :2x - 2y + z + 3 = 0\). Gọi $M(a ; b ; c)$ là điểm trên mặt cầu $(S)$ sao cho khoảng cách từ $M$ đến mặt phẳng $(P)$ là lớn nhất. Khi đó:
Giả sử $M(a;b;c)$ là điểm cần tìm.
Mặt cầu $(S)$ có tâm $I(1;2;3)$ bán kính $R=3 $.
Gọi $Δ$ là đường thẳng qua $I$ và vuông góc với $mp(P)$.
\( \Rightarrow \)\(\Delta :\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 2t\\z = 3 + t\end{array} \right.\)
Đường thẳng $Δ$ cắt mặt cầu tại 2 điểm $A, B$. Toạ độ $A, B$ là nghiệm của hệ:
\(\left\{ \begin{array}{l}x = 1 + 2t\\y = 2 - 2t\\z = 3 + t\\{(x - 1)^2} + {(y - 2)^2} + {(z - 3)^2} = 9\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}A\left( {3;0;4} \right)\\B\left( { - 1;4;2} \right)\;\end{array} \right.\)
Ta có: $d\left( {A;\left( P \right)} \right) = \dfrac{{\left| {2.3 - 2.0 + 4 + 3} \right|}}{{\sqrt {{2^2} + {2^2} + 1} }} = \dfrac{{13}}{3}$ và $d\left( {B;\left( P \right)} \right) = \dfrac{{\left| {2.( - 1) - 2.4 + 2 + 3} \right|}}{{\sqrt {{2^2} + {2^2} + 1} }} = \dfrac{5}{3}$
Do đó điểm cần tìm là điểm $A≡M \Rightarrow a+b+c= 3+0+4= 7$.
Cho điểm $A(0 ; 8 ; 2)$ và mặt cầu $(S)$ có phương trình \((S):{\left( {x - 5} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 7} \right)^2} = 72\) và điểm $B(1 ; 1 ; -9)$. Viết phương trình mặt phẳng $(P)$ qua $A$ tiếp xúc với $(S)$ sao cho khoảng cách từ $B$ đến $(P)$ là lớn nhất. Giả sử \(\overrightarrow n = \left( {1;m;n} \right)\) là véctơ pháp tuyến của $(P)$. Lúc đó:
$(S)$ có tâm $I(5;-3;7)$ và bán kính $R= 6\sqrt 2 $
Theo đề bài ta có phương trình $(P)$ có dạng $x+m(y-8)+n(z-2)=0$
Vì $(P)$ tiếp xúc với $(S) $ nên ${\rm{d}}(I,(P)) = \dfrac{{\left| {5 + m( - 3 - 8) + n(7 - 2)} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = \dfrac{{\left| {5 - 11m + 5n} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = 6\sqrt 2 $
$\begin{array}{l} \Leftrightarrow \left| {5 - 11m + 5n} \right| = 6\sqrt 2 .\sqrt {1 + {m^2} + {n^2}} \\ \Leftrightarrow 25 + 121{m^2} + 25{n^2} - 110m + 50n - 110mn = 72(1 + {m^2} + {n^2})\\ \Leftrightarrow 49{m^2} - 110m + 50n - 110mn - 47{n^2} - 47 = 0\\ \Leftrightarrow 49{m^2} - 110m(n + 1) - 47{n^2} + 50n - 47 = 0(1)\\\Delta ' = 3025{(n + 1)^2} - 49( - 47{n^2} + 50n - 47) = 5328{n^2} + 3600n + 5328 > 0\end{array}$
Phương trình (*) luôn có nghiệm
$\begin{array}{l}{\rm{d}}(B,(P)) = \dfrac{{\left| {1 + m(1 - 8) + n( - 9 - 2)} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = \dfrac{{\left| {1 - 7m - 11n} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }}\\ = > d(B,(P))\max = AB \Leftrightarrow \dfrac{{\left| {1 - 7m - 11n} \right|}}{{\sqrt {1 + {m^2} + {n^2}} }} = 3\sqrt {19} \Leftrightarrow \sqrt {1 + {m^2} + {n^2}} = \dfrac{{\left| {1 - 7m - 11n} \right|}}{{3\sqrt {19} }}\end{array}$
Mặt khác $\dfrac{{\left| {5 - 11m + 5n} \right|}}{{6\sqrt 2 }} = \sqrt {1 + {m^2} + {n^2}} $
$\dfrac{{\left| {1 - 7m - 11n} \right|}}{{3\sqrt {19} }}$=$\dfrac{{\left| {5 - 11m + 5n} \right|}}{{6\sqrt 2 }}$
$\begin{array}{l}72(1 + 49{m^2} + 121{n^2} - 14m - 22n + 154mn) = 171(25 + 121{m^2} + 25{n^2} - 110m + 50n - 110mn)\\ \Leftrightarrow 8(1 + 49{m^2} + 121{n^2} - 14m - 22n + 154mn) = 19(25 + 121{m^2} + 25{n^2} - 110m + 50n - 110mn)\\ \Leftrightarrow - 1907{m^2} + 493{n^2} + 1978m - 1126n + 3322mn - 467 = 0(2)\end{array}$
Từ (1) và (2) $\Rightarrow m.n= \dfrac{{276}}{{49}}$
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 6x - 4z + 9 - {m^2} = 0\). Gọi T là tập các giá trị của \(m\) để mặt cầu \(\left( S \right)\) tiếp xúc với mặt phẳng \(\left( {Oyz} \right)\). Tích các giá trị của \(m\) trong \(T\) bằng:
Mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} + 6x - 4z + 9 - {m^2} = 0\) có tâm \(I\left( { - 3;0;2} \right)\) và bán kính \(R = \sqrt {{m^2} + 4} \)
Mặt phẳng \(\left( {Oyz} \right)\) có phương trình là \(x = 0 \Rightarrow d\left( {I;\left( {Oyz} \right)} \right) = \frac{{\left| { - 3} \right|}}{1} = 3\)
\( \Rightarrow R = \sqrt {{m^2} + 4} = 3 \Leftrightarrow m = \pm \sqrt 5 \)
Tích các giá trị của m là \(\sqrt 5 .\left( { - \sqrt 5 } \right) = - 5\).
Trong không gian \(Oxyz\), cho đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{{ - 2}} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) và mặt phẳng \(\left( P \right):\,\,2x - y + z - 3 = 0\). Gọi \(\left( S \right)\) là mặt cầu có tâm \(I\) thuộc \(\Delta \) và tiếp xúc với \(\left( P \right)\) tại điểm \(H\left( {1; - 1;0} \right)\). Phương trình của \(\left( S \right)\) là:
Vì \(I \in \Delta :\,\,\dfrac{{x - 1}}{{ - 2}} = \dfrac{y}{2} = \dfrac{{z - 2}}{1}\) nên ta gọi \(I\left( {1 - 2t;\,\,2t;\,\,2 + t} \right)\).
Vì \(\left( S \right)\) tiếp xúc với \(\left( P \right):\,\,2x - y + z - 3 = 0\) tại điểm \(H\left( {1; - 1;0} \right)\) nên ta có: \(d\left( {I;\left( P \right)} \right) = IH = R\).
\(\begin{array}{l} \Leftrightarrow \dfrac{{\left| {2.\left( {1 - 2t} \right) - 2t + 2 + t - 3} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \sqrt {{{\left( {2t} \right)}^2} + {{\left( { - 1 - 2t} \right)}^2} + {{\left( { - 2 - t} \right)}^2}} \\ \Leftrightarrow \dfrac{{\left| { - 5t + 1} \right|}}{{\sqrt 6 }} = \sqrt {9{t^2} + 8t + 5} \\ \Leftrightarrow 25{t^2} - 10t + 1 = 54{t^2} + 48t + 30\\ \Leftrightarrow 29{t^2} + 58t + 29 = 0\\ \Leftrightarrow {t^2} + 2t + 1 = 0\\ \Leftrightarrow {\left( {t + 1} \right)^2} = 0\\ \Leftrightarrow t = - 1\end{array}\)
\( \Rightarrow I\left( {3; - 2;1} \right)\) và \(R = IH = \sqrt 6 \).
Vậy phương trình mặt cầu \(\left( S \right)\) là: \({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 1} \right)^2} = 6\).
Trong không gian với hệ tọa độ \(Oxyz\), cho mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 8x + 2y + 2z - 3 = 0\) và đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{3} = \dfrac{y}{{ - 2}} = \dfrac{{z + 2}}{{ - 1}}\). Mặt phẳng \(\left( \alpha \right)\) vuông góc với \(\Delta \) và cắt \(\left( S \right)\) theo giao tuyến là đường tròn \(\left( C \right)\) có bán kính lớn nhất. Phương trình \(\left( \alpha \right)\) là:
Đường thẳng \(\Delta :\,\,\dfrac{{x - 1}}{3} = \dfrac{y}{{ - 2}} = \dfrac{{z + 2}}{{ - 1}}\) có 1 VTCP là \(\overrightarrow u = \left( {3; - 2; - 1} \right)\).
Vì \(\left( \alpha \right) \bot \Delta \) nên mặt phẳng \(\left( \alpha \right)\) có 1 VTPT là \(\overrightarrow n = \overrightarrow u = \left( {3; - 2; - 1} \right)\). Khi đó phương trình mặt phẳng \(\left( \alpha \right)\) có dạng \(3x - 2y - z + d = 0\).
Mặt cầu \(\left( S \right):\,\,{x^2} + {y^2} + {z^2} - 8x + 2y + 2z - 3 = 0\) có tâm \(I\left( {4; - 1; - 1} \right)\), bán kính \(R = \sqrt {16 + 1 + 1 + 3} = \sqrt {21} \).
Gọi \(r\) là bán kính đường tròn \(\left( C \right)\), \(d = d\left( {I;\left( \alpha \right)} \right)\).
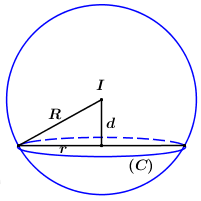
Áp dụng định lí Pytago ta có: \({R^2} = {r^2} + {d^2}\), do đó để \(r\) đạt GTLN thì \(d\) phải đạt GTNN (vì \(R = \sqrt {21} \) không đổi).
Ta có: \(d = \dfrac{{\left| {3.4 - 2.\left( { - 1} \right) - 1.\left( { - 1} \right) + d} \right|}}{{\sqrt {{3^2} + {{\left( { - 2} \right)}^2} + {{\left( { - 1} \right)}^2}} }} = \dfrac{{\left| {15 + d} \right|}}{{\sqrt {14} }} \ge 0\), suy ra \({d_{\min }} = 0 \Leftrightarrow d = - 15\).
Vậy phương trình mặt phẳng \(\left( \alpha \right)\) cần tìm là: \(3x - 2y - z - 15 = 0\).
Trong không gian \(Oxyz\), cho mặt cầu \(\left( C \right):\,\,\,{\left( {x + 1} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z - 2} \right)^2} = 1\) và hai điểm \(A\left( {2;1;0} \right)\), \(B\left( {0;2;0} \right)\). Khi điểm \(S\) thay đổi trên mặt cầu \(\left( C \right)\), thể tích của khối chóp \(S.OAB\) có giá trị lớn nhất bằng bao nhiêu?
Bước 1:
Dễ dàng nhận thấy \(O,\,\,A,\,\,B\) đều nằm ngoài mặt cầu \(\left( C \right)\) nên \(\left( {OAB} \right)\) không cắt mặt cầu \(\left( C \right)\).

Mặt cầu \(\left( C \right)\) ta có tâm \(I\left( { - 1;3;2} \right)\), bán kính \(R = 1\).
Ta có \(\overrightarrow {OA} = \left( {2;1;0} \right),\,\,\overrightarrow {OB} = \left( {0;2;0} \right) \Rightarrow \left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right] = \left( {0;0;4} \right)\)
\( \Rightarrow {S_{\Delta OAB}} = \dfrac{1}{2}\left| {\left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right]} \right| = 2\)
Bước 2:
\( \Rightarrow {V_{S.OAB}} = \dfrac{1}{3}d\left( {S;\left( {OAB} \right)} \right).{S_{\Delta OAB}}\).
Vì \({S_{\Delta OAB}}\) không đổi nên \({V_{S.OAB}}\) đạt giá trị lớn nhất khi và chỉ khi \(d\left( {S;\left( {OAB} \right)} \right)\) lớn nhất, khi đó \(d\left( {S;\left( {OAB} \right)} \right) = R + d\left( {I;\left( {OAB} \right)} \right)\).
Bước 3:
Mặt phẳng \(\left( {OAB} \right)\) nhận \(\overrightarrow n = \dfrac{1}{4}\left[ {\overrightarrow {OA} ;\overrightarrow {OB} } \right] = \left( {0;0;1} \right)\) là 1 VTPT nên có phương trình: \(z = 0\).
\( \Rightarrow d\left( {I;\left( {OAB} \right)} \right) = \left| {{z_I}} \right| = 2\) \( \Rightarrow d{\left( {S;\left( {OAB} \right)} \right)_{\max }} = 1 + 2 = 3\).
Vậy \(\max {V_{S.OAB}} = \dfrac{1}{3}.3.2 = 2\).

