Bài toán cực trị có tham số đối với một số hàm số cơ bản

TXĐ: $D = R$

TH1: $m = 0 \to y = x - 1.$

Hàm số không có cực trị.

TH2: $m \ne 0$.

Ta có: $y = \dfrac{{m{x^3}}}{3} - m{x^2} + x - 1$ $ \Rightarrow y' = m{x^2} - 2mx + 1.$

Để hàm số cho có cực đại, cực tiểu thì phương trình $y' = 0$ phải có $2$ nghiệm phân biệt

$ \Rightarrow \Delta ' = {m^2} - m > 0 \Leftrightarrow \left[ \begin{gathered} m < 0 \hfill \\ m > 1 \hfill \\\end{gathered}  \right..$

$y =  - {x^4} + 2m{x^2}$ $ \Rightarrow y' =  - 4{x^3} + 4mx =  - 4x\left( {{x^2} - m} \right)$ $ \Rightarrow y' = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\{x^2} = m \hfill \\ \end{gathered}  \right.$

Để hàm số có ba điểm cực trị thì phương trình $y' = 0$ có ba nghiệm phân biệt hay phương trình $x^2=m$ có hai nghiệm phân biệt $\ne 0$ hay $m > 0$

$y' = 8{x^3} - 2\left( {m + 1} \right)x = 2x\left[ {4{x^2} - \left( {m + 1} \right)} \right]$  $ \Rightarrow y' = 0 \Leftrightarrow \left[ \begin{gathered} x = 0 \hfill \\4{x^2} = m + 1{\text{ }}(1) \hfill \\ \end{gathered}  \right.$ 

Ta có yêu cầu bài toán để hàm số có một điểm cực trị $ \Leftrightarrow y' = 0$ có $1$ nghiệm duy nhất $ \Leftrightarrow (1)$ có $1$ nghiệm $x = 0$ hoặc $(1)$ vô nghiệm $ \Leftrightarrow m + 1 \leqslant 0 \Leftrightarrow m \leqslant  - 1$ 

Ta có: $f(x) = {x^3} + a{x^2} + bx - 2$

$ + )f\left( 0 \right) =  - 2 < 0;$ $f(1) = a + b - 1 > 0$ nên \(f\left( 0 \right).f\left( 1 \right) < 0\)

\( \Rightarrow \) phương trình \(f\left( x \right) = 0\) có ít nhất \(1\) nghiệm \({x_1} \in \left( {0;1} \right)\)

\( + )f\left( 2 \right) = 2\left( {3 + 2a + b} \right) < 0\) nên \(f\left( 1 \right).f\left( 2 \right) < 0\)

\( \Rightarrow \) phương trình \(f\left( x \right) = 0\) có ít nhất \(1\) nghiệm \({x_2} \in \left( {1;2} \right)\)

Do đó phương trình \(f\left( x \right) = 0\) có ít nhất hai nghiệm và đồ thị hàm số \(y = f\left( x \right)\) chỉ có thể có dạng:

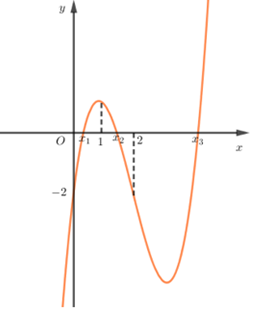
Khi đó, đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\)(màu tím) và \(y = \left| {f\left( {\left| x \right|} \right)} \right|\) (màu cam) lần lượt có đồ thị như sau:

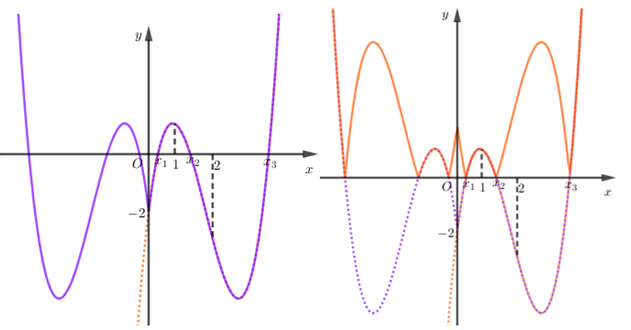
Như vậy, hàm số $y = \left| {f\left( {\left| x \right|} \right)} \right|$ có tất cả $11$ cực trị.

TXĐ $D = \mathbb{R}$

$y' =  - {x^2} + \dfrac{2}{3}mx \Rightarrow y'' =  - 2x + \dfrac{2}{3}m$

Hàm số đã cho đạt cực đại tại $x = 2$

$ \Leftrightarrow \left\{ \begin{gathered}  y'(2) = 0 \hfill \\ y''\left( 2 \right) < 0 \hfill \\ \end{gathered}  \right. $ $\Leftrightarrow \left\{ \begin{gathered} - {2^2} + \dfrac{2}{3}m.2 = 0 \hfill \\ - 2.2 + \dfrac{2}{3}m. < 0 \hfill \\ \end{gathered}  \right. $ $\Leftrightarrow \left\{ \begin{gathered} - 4 + \dfrac{4}{3}m = 0 \hfill \\- 4 + \dfrac{2}{3}m < 0 \hfill \\ \end{gathered}  \right. $ $\Leftrightarrow \left\{ \begin{gathered} m = 3 \hfill \\m < 6 \hfill \\ \end{gathered}  \right. \Leftrightarrow m = 3$

TXĐ: $D = R$

Ta có: $y' = 3{x^2} - 4mx + {m^2} \Rightarrow y'' = 6x - 4m$

Để $x = 1$ là điểm cực tiểu của hàm số  thì:

$\left\{ \begin{gathered}y'\left( 1 \right) = 0 \hfill \\y''\left( 1 \right) > 0 \hfill \\ \end{gathered}  \right. \Leftrightarrow \left\{ \begin{gathered}  {m^2} - 4m + 3 = 0 \hfill \\ 6 - 4m > 0 \hfill \\ \end{gathered}  \right. \Leftrightarrow \left\{ \begin{gathered}m = 1;m = 3 \hfill \\m < \dfrac{3}{2} \hfill \\ \end{gathered}  \right. \Leftrightarrow m = 1.$

Đạo hàm : $y' = {x^2} - 2ax - 3a$, $y' = 0 \Leftrightarrow {x^2} - 2ax - 3a = 0$  $\left( 1 \right)$

Hàm số có hai cực trị ${x_1}$,${x_2}$ khi $y' = 0$ có hai nghiệm phân biệt $ \Leftrightarrow \Delta ' > 0 \Leftrightarrow a <  - 3 $ hoặc $ a > 0$

Khi đó ${x_1}$,${x_2}$ là nghiệm pt $\left( 1 \right)$, theo định lý Viet : $\left\{ \begin{array}{l}{x_1} + {x_2} = 2a\\{x_1}.{x_2} =  - 3a\end{array} \right.$

Do đó, thay $\left\{ \begin{array}{l}2a={x_1} + {x_2} \\3a=-{x_1}.{x_2} \end{array} \right.$ vào đẳng thức bài cho ta được:

$\left\{ \begin{array}{l}x_1^2 + 2a{x_2} + 9a = x_1^2 + \left( {{x_1} + {x_2}} \right){x_2} - 3{x_1}{x_2} = x_1^2 - 2{x_1}{x_2} + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 4{a^2} + 12a\\x_2^2 + 2a{x_1} + 9a = x_2^2 + \left( {{x_1} + {x_2}} \right){x_1} - 3{x_1}{x_2} = x_1^2 - 2{x_1}{x_2} + x_2^2 = {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} = 4{a^2} + 12a\end{array} \right.$

Theo đề bài, ta có : $\dfrac{{4a + 12}}{a} + \dfrac{a}{{4a + 12}} = 2 \Leftrightarrow \dfrac{{4a + 12}}{a} = 1 \Leftrightarrow a =  - 4$

\(y' = 4{x^3} - 4{m^2}x\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm m.\end{array} \right.\)

Để hàm số có 3 cực trị thì phương trình \(y' = 0\) có 3 nghiệm, hay \(m \ne 0\).

Không mất tính tổng quát giả sử 3 điểm cực trị có tọa độ \(A\left( {0;\,\,{m^4} + 3} \right)\); \(B\left( {m;3} \right)\);\(C\left( { - m;3} \right)\).

Ta có \(\overrightarrow {AC} \left( { - m; - {m^4}} \right);\,\,\overrightarrow {OC} \left( { - m;3} \right)\)

Tứ giác \(OBAC\) có \(\left\{ \begin{array}{l}AB = AC\\OB = OC\end{array} \right.\).

Suy ra \(OA\) là đường trung trực của \(BC\).

Để tứ giác \(OBAC\) nội tiếp đường tròn thì điểm \(B\), \(C\) phải nhìn cạnh \(OA\) dưới góc \(90^\circ .\)

Khi đó \(\overrightarrow {AC} .\overrightarrow {OC}  = 0 \Leftrightarrow {m^2} - 3{m^4} = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0:L\\m =  \pm \sqrt {\dfrac{1}{3}} :T/m\end{array} \right.\).

Ta có \(y' = {x^3}\left[ {8{x^4} + 5x\left( {m - 2} \right) - 4\left( {{m^2} - 4} \right)} \right] = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\g\left( x \right) = 8{x^4} + 5x\left( {m - 2} \right) - 4\left( {{m^2} - 4} \right) = 0\end{array} \right.\)

Do \(x = 0\) là một nghiệm của đạo hàm nên hàm số đạt cực tiểu tại \(x = 0 \Leftrightarrow y'\) đổi dấu từ \( - \) sang \( + \) khi qua nghiệm \(x = 0\)

*) TH1: \(x = 0\) là nghiệm của \(g\left( x \right)\) hay \(m =  \pm 2\)

Với $m{\rm{ }} = {\rm{ }}2$  thì $g\left( x \right) = 0$  có nghiệm $x = 0$  bội $4$ theo kết quả ở trên thì $x{\rm{ }} = {\rm{ }}0$  là nghiệm bội $7$  của $y'$  nên $x{\rm{ }} = {\rm{ }}0$ là điểm cực tiểu của hàm số nên chọn $m{\rm{ }} = {\rm{ }}2.$

Với $m =  - 2$ thì $g\left( x \right)$ có nghiệm $x{\rm{ }} = {\rm{ }}0$ và 1 nghiệm dương, lúc này $x{\rm{ }} = {\rm{ }}0$ là nghiệm bội \(4\) của \(f'\left( x \right)\) nên \(x = 0\) không là điểm cực trị của hàm số. Loại $m{\rm{ }} = {\rm{ }} - {\rm{ }}2.$

*) TH2: \(x = 0\) không là nghiệm của \(g\left( x \right)\) hay $m \ne  \pm 2$. Ta có \(g\left( 0 \right) =  - 4\left( {{m^2} - 4} \right)\).

\(y' = {x^3}g\left( x \right)\) đổi dấu từ \( - \) sang \( + \) qua nghiệm \(x = 0\) khi và chỉ khi \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} g\left( x \right) > 0\\\mathop {\lim }\limits_{x \to {0^ - }} g\left( x \right) > 0\end{array} \right.\)

\( \Leftrightarrow  - 4\left( {{m^2} - 4} \right) > 0\)\( \Leftrightarrow {m^2} - 4 < 0 \Leftrightarrow  - 2 < m < 2\)

Do \(m\) nguyên nên \(m \in \left\{ { - 1;0;1} \right\}\)

Kết hợp hai trường hợp ta được \(m \in \left\{ { - 1;0;1;2} \right\}\)

$y = {x^3} - \left( {3m + 1} \right){x^2} + \left( {{m^2} + 3m + 2} \right)x + 3$

$y' = 3{x^2} - \left( {6m + 2} \right)x + {m^2} + 3m + 2$

Để cực tiểu và cực đại của đồ thị hàm số $y$ nằm về hai phía của trục tung thì ${x_1}{x_2} < 0,$ với ${x_1},{x_2}$ là hai nghiệm của phương trình $y' = 0.$

$ \Leftrightarrow 3({m^2} + 3m + 2) < 0 \Leftrightarrow {m^2} + 3m + 2 < 0 \Leftrightarrow  - 2 < m <  - 1$

\(y' = {x^2} - 2mx + 2m - 4\)

Để hàm số có cực đại cực tiểu \( \Leftrightarrow \Delta ' > 0,\forall m \Leftrightarrow {m^2} - 2m + 4 > 0,\forall m\)

Khi đó phương trình $y'=0$ có hai nghiệm $x_1,x_2$ thỏa mãn 

\(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a} = 2m\\{x_1}{x_2} = \dfrac{c}{a} = 2m - 4\end{array} \right.\)

Ta có:

\(\begin{array}{l}x_1^2 + x_2^2 = {x_1}.{x_2} + 10\\ \Leftrightarrow {({x_1} + {x_2})^2} - 2{x_1}{x_2} - {x_1}{x_2} - 10 = 0\\ \Leftrightarrow {({x_1} + {x_2})^2} - 3{x_1}{x_2} - 10 = 0\\ \Leftrightarrow {(2m)^2} - 3.(2m - 4) - 10 = 0\\ \Leftrightarrow 4{m^2} - 6m + 2 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = \dfrac{1}{2}\end{array} \right.\end{array}\)

Ta có: $y' = 3{x^2} - 6x + 3m$ 

Hàm số có $2$ điểm cực trị nhỏ hơn $2$ $ \Leftrightarrow y'$ có $2$ nghiệm phân biệt ${x_1},\,{x_2}$ thoả mãn ${x_1} < {x_2} < 2$ $ \Leftrightarrow \left\{ \begin{gathered}\Delta ' > 0 \hfill \\a.f(2) > 0 \hfill \\\dfrac{S}{2} < 2 \hfill \\\end{gathered}  \right. $ $\Leftrightarrow \left\{ \begin{gathered}9 - 9m > 0 \hfill \\ 3.({3.2^2} - 6.2 + 3m) > 0 \hfill \\ 1 < 2(\forall m) \hfill \\ \end{gathered}  \right.$ $ \Leftrightarrow \left\{ \begin{gathered}  m < 1 \hfill \\  m > 0 \hfill \\ \end{gathered}  \right. $ $\Leftrightarrow 0 < m < 1$

Ta có: $y' = 4{x^3} - 4mx = 0 \Leftrightarrow \left[ \begin{gathered}  x = 0 \hfill \\ {x^2} = m \hfill \\ \end{gathered}  \right.$

Đồ thị hàm số có $3$ điểm cực trị $ \Leftrightarrow $ pt $y' = 0$ có $3$ nghiệm phân biệt $ \Leftrightarrow $$m > 0$$ \Rightarrow \left[ \begin{gathered}x = 0 \hfill \\x = \sqrt m  \hfill \\ x =  - \sqrt m  \hfill \\ \end{gathered}  \right.$

$ \Rightarrow $ Đồ thị hàm số có $3$ điểm cực trị là: $A(0;2);\,\,\,B( - \sqrt m ;2 - {m^2});\,\,C(\sqrt m ;2 - {m^2})$

\(\overrightarrow {AB}  = \left( { - \sqrt m ; - {m^2}} \right),\overrightarrow {AC}  = \left( {\sqrt m ; - {m^2}} \right)\)

Dễ thấy $∆ ABC$ cân tại $A,$ để $∆ ABC$ vuông cân thì nó phải vuông tại $A$ 

\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC}  = 0 \Leftrightarrow  - m + {m^4} = 0\) \( \Leftrightarrow m\left( {{m^3} - 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\{m^3} - 1 = 0\end{array} \right.\) \( \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 1\end{array} \right.\) 

Kết hợp điều kiện $m > 0$ ta có $m = 1$

Vì điểm \(M\left( {a;\,\,b} \right)\) thuộc đồ thị \(\left( {{C_m}} \right)\) nên ta có: \({\left( {a - m} \right)^3} - 3a + {m^2} = b,\forall m \in \mathbb{R}\). \(\left( 1 \right)\)

Xét \(y' = 3{\left( {x - m} \right)^2} - 3\); \(y' = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x = m - 1\\x = m + 1\end{array} \right.\).

Bảng biến thiên

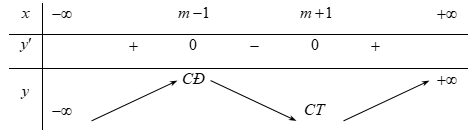
Dựa vào bảng biến thiên, ta có:

Nếu \({m_1}\) là giá trị của tham số \(m\) để đồ thị hàm số nhận điểm $M\left( {a;\,\,b} \right)$ là điểm cực đại thì \(a = {m_1} - 1\). Nếu \({m_2}\) là giá trị của tham số \(m\) để đồ thị hàm số nhận điểm $M\left( {a;\,\,b} \right)$ là điểm cực tiểu thì \(a = {m_2} + 1\)

Do đó $m_1=a+1,m_2=a-1$

Mà \({m_1}\), \({m_2}\) phải thỏa mãn \(\left( 1 \right)\) nên ta có: \(\left\{ \begin{array}{l} - 1 - 3a + {\left( {a + 1} \right)^2} = b\\1 - 3a + {\left( {a - 1} \right)^2} = b\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}a = \dfrac{1}{2}\\b =  - \dfrac{1}{4}\end{array} \right.\)

Vậy \(S = 2018a + 2020b = 504\)

\(\begin{array}{l}y' = 4{x^3} - 4mx\\y' = 0 \Leftrightarrow 4{x^3} - 4mx = 0 \Leftrightarrow 4x\left( {{x^2} - m} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = m\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm \sqrt m \,\, (1)\end{array} \right.\end{array}\)

Hàm số \(y=f(x)\) có 3 cực trị

\( \Leftrightarrow y' = 0\) có 3 nghiệm phân biệt

\( \Leftrightarrow (1){\rm{\;}}\) có 2 nghiệm phân biệt khác 0

\( \Leftrightarrow \) \(m > 0\).

Gọi 3 điểm cực trị của hàm số lần lượt là \(A(0;a);B(-\sqrt m;b);C(\sqrt m;c)\). Khi đó:

\(\begin{array}{*{20}{l}}
{ + )x = 0 \Rightarrow A\left( {0;3m + 2} \right)}\\
{ + )x = - \sqrt m {\rm{\;}} \Rightarrow y = {{\left( { - \sqrt m } \right)}^4} - 2m.{{\left( { - \sqrt m } \right)}^2} + 3m + 2}\\
{ = {m^2} - 2{m^2} + 3m + 2}\\
{ = {\rm{\;}} - {m^2} + 3m + 2 \Rightarrow B\left( { - \sqrt m ; - {m^2} + 3m + 2} \right)}\\
{ + )x = \sqrt m {\rm{\;}} \Rightarrow y=- {m^2} + 3m + 2\\ \Rightarrow C\left( {\sqrt m ; - {m^2} + 3m + 2} \right)}
\end{array}\)

Ta luôn có $AB=AC$ nên tam giác $ABC$ đều

\(\begin{array}{l} \Leftrightarrow AB = BC \Leftrightarrow A{B^2} = B{C^2}\\ \Leftrightarrow {\left( { - \sqrt m } \right)^2} + {\left( { - {m^2}} \right)^2} = {\left( {2\sqrt m } \right)^2} + {0^2}\\ \Leftrightarrow m + {m^4} = 4m\\ \Leftrightarrow {m^4} - 3m = 0\\ \Leftrightarrow m\left( {{m^3} - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = \sqrt[3]{3}\end{array} \right.\end{array}\) 

Kết hợp điều kiện \(m > 0 \Rightarrow m = \sqrt[3]{3}\)

\(\begin{array}{l}y' = 4{x^3} + 4\left( {1 - {m^2}} \right)x\\y' = 0 \Leftrightarrow 4{x^3} + 4\left( {1 - {m^2}} \right)x = 0 \Leftrightarrow 4x\left( {{x^2} + 1 - {m^2}} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = {m^2} - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm \sqrt {{m^2} - 1} \end{array} \right.\end{array}\)

Điều kiện để hàm số có $3$ cực trị: \({m^2} - 1 > 0 \Leftrightarrow \left[ \begin{array}{l}m > 1\\m <  - 1\end{array} \right.\)

\(\begin{array}{l}x = 0 \Rightarrow A\left( {0;m + 1} \right)\\x =  - \sqrt {{m^2} - 1}  \Rightarrow y = {\left( { - \sqrt {{m^2} - 1} } \right)^4} + 2\left( {1 - {m^2}} \right){\left( { - \sqrt {{m^2} - 1} } \right)^2} + m + 1\\ \Rightarrow y = {\left( {{m^2} - 1} \right)^2} - 2{\left( {{m^2} - 1} \right)^2} + m + 1 =  - {\left( {{m^2} - 1} \right)^2} + m + 1\\ \Rightarrow B\left( { - \sqrt {{m^2} - 1} ; - {{\left( {{m^2} - 1} \right)}^2} + m + 1} \right)\\x = \sqrt {{m^2} - 1}  \Rightarrow C\left( {\sqrt {{m^2} - 1} ; - {{\left( {{m^2} - 1} \right)}^2} + m + 1} \right)\end{array}\)

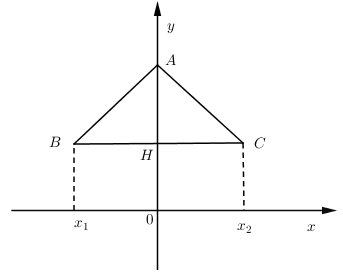
\(\begin{array}{l}{S_{ABC}} = 4\sqrt 2  \Leftrightarrow \dfrac{1}{2}AH.BC = 4\sqrt 2 \\ \Leftrightarrow \left| {{y_A} - {y_C}} \right|.\left| {HC} \right| = 4\sqrt 2 \\ \Leftrightarrow \left| {{y_A} - {y_C}} \right|.\left| {{x_C}} \right| = 4\sqrt 2 \\ \Leftrightarrow \left| {m + 1 + {{\left( {{m^2} - 1} \right)}^2} - m - 1} \right|.\sqrt {{m^2} - 1}  = 4\sqrt 2 \\ \Leftrightarrow {\left( {{m^2} - 1} \right)^2}.\sqrt {{m^2} - 1}  = 4\sqrt 2 \\ \Leftrightarrow {\left( {{m^2} - 1} \right)^5} = 32 \Leftrightarrow {m^2} - 1 = 2 \Leftrightarrow {m^2} = 3 \Leftrightarrow m =  \pm \sqrt 3 \end{array}\)

\(m =  \pm \sqrt 3 \) thỏa mãn điều kiện\(\left[ \begin{array}{l}m > 1\\m <  - 1\end{array} \right.\)

\(\begin{array}{l}y' = 4{x^3} - 4mx\\y' = 0 \Leftrightarrow 4{x^3} - 4mx = 0 \Leftrightarrow 4x\left( {{x^2} - m} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm \sqrt m \end{array} \right.\end{array}\)

Điều kiện để hàm số có $3$ cực trị: \(m > 0\)

\(\begin{array}{l}x = 0 \Rightarrow A\left( {0;\,{m^2} + m} \right)\\x =  - \sqrt m  \Rightarrow y = {\left( { - \sqrt m } \right)^4} - 2m{\left( { - \sqrt m } \right)^2} + {m^2} + m \\= {m^2} - 2{m^2} + {m^2} + m = m \Rightarrow B\left( { - \sqrt m ;\,m} \right)\\x = \sqrt m  \Rightarrow C\left( {\sqrt m ;\,m} \right)\end{array}\)

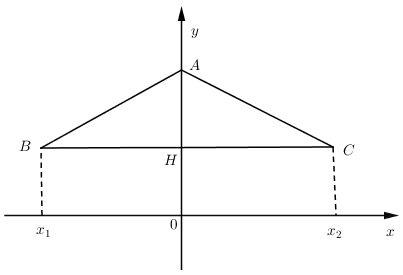
$\begin{array}{l}
\overrightarrow {AB} = \left( { - \sqrt m ; - {m^2}} \right),\overrightarrow {AC} = \left( {\sqrt m ; - {m^2}} \right)\\
\widehat {BAC} = {120^0}\\
\Leftrightarrow \dfrac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{\left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|}} = \cos {120^0}\\
\Leftrightarrow \dfrac{{ - m + {m^4}}}{{\sqrt {m + {m^4}} .\sqrt {m + {m^4}} }} = - \dfrac{1}{2}\\
\Leftrightarrow 2\left( {{m^4} - m} \right) = - \left( {m + {m^4}} \right)\\
\Leftrightarrow 3{m^4} - m = 0\\
\Leftrightarrow m\left( {3{m^3} - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
m = 0\left( {loai} \right)\\
m = \dfrac{1}{{\sqrt[3]{3}}}
\end{array} \right.
\end{array}$

Tập xác định \(D = \mathbb{R}\).

Ta có \(y' = 4{x^3} - 4mx = 4x\left( {{x^2} - m} \right)\).

Đồ thị hàm số có ba điểm cực trị $ \Leftrightarrow m \ge 0$

Khi đó: $y' = 4m{x^3} - 4mx = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  \pm \sqrt m \end{array} \right.$

Suy ra: Đồ thị hàm số có ba điểm cực trị là $A\left( {0;m - 1} \right)$ $B\left( { - \sqrt m ; - {m^2} + m - 1} \right)$, $C\left( {\sqrt m ; - {m^2} + m - 1} \right)$

Ta có: ${S_{\Delta ABC}} = \dfrac{1}{2}\left| {{y_B} - {y_A}} \right|.\left| {{x_C} - {x_B}} \right| = {m^2}\sqrt m $;

$AB = AC = \sqrt {{m^4} + m} $; $BC = 2\sqrt m $

Gọi \(R=1\) là bán kính đường tròn ngoại tiếp tam giác \(ABC\)

Diện tích tam giác \(ABC\) là:

\({S_{\Delta ABC}} = \dfrac{{AB.AC.BC}}{{4R}} = \dfrac{{2\sqrt m \left( {{m^4} + m} \right)}}{4}\)

Suy ra \({m^2}\sqrt m  = \dfrac{{2\sqrt m \left( {{m^4} + m} \right)}}{4} \Leftrightarrow 2m = {m^3} + 1\)

\( \Leftrightarrow \left( {m - 1} \right)\left( {{m^2} + m - 1} \right) = 0\)

\( \Leftrightarrow \left[ \begin{array}{l}m = 1\\{m^2} + m - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = \dfrac{{ - 1 + \sqrt 5 }}{2}\\m = \dfrac{{ - 1 - \sqrt 5 }}{2}\,\,\left( l \right)\end{array} \right.\)

Vậy: \(m = 1\) hoặc \(m = \dfrac{{ - 1 + \sqrt 5 }}{2}\)

Có: $y\left( x \right) = {x^3} + 3m{x^2} - 3x$ $ \Rightarrow y'\left( x \right) = 3{x^2} + 6mx - 3$ 

Phương trình đường thẳng $d$ đi qua $2$ cực trị của $(C)$ nên $\left( {{x_o};{y_o}} \right) \in d$  thỏa mãn:

\(\begin{array}{l}\left\{ \begin{array}{l}y'\left( {{x_o}} \right) = 0\\{y_o} = x_o^3 + 3mx_0^2 - 3{x_o}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x_o^2 + 6m{x_o} - 3 = 0\\{y_o} = {x_o}\left( {x_o^2 + 2m{x_o}} \right) - 3{x_0} + mx_0^2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x_o^2 + 2m{x_o} = 1\\{y_o} =  - 2{x_o} + mx_o^2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x_o^2 =  - 2m{x_o} + 1\\{y_o} =  - 2{x_o} + m\left( { - 2m{x_o} + 1} \right)\end{array} \right.\\ \Rightarrow {y_o} =  - 2\left( {{m^2} + 1} \right){x_o} + m\end{array}\)

$y' = 6{x^2} - 6\left( {m + 1} \right)x + 6m$

Đồ thị hàm số có hai điểm cực trị \(A,B\) \( \Leftrightarrow \) phương trình \(y' = 0\) có hai nghiệm phân biệt

\( \Leftrightarrow \Delta ' = 9{\left( {m + 1} \right)^2} - 36m > 0\) \( \Leftrightarrow 9{m^2} - 18m + 9 > 0\) \( \Leftrightarrow 9{\left( {m - 1} \right)^2} > 0\) \( \Leftrightarrow m \ne 1\)

Khi đó,

$y = y'.\left( \dfrac{1}{3}x -\dfrac{{m + 1}}{6} \right) + \left[ {4m - {{\left( {m + 1} \right)}^2}} \right]x + m\left( {m + 1} \right)$

Đường thẳng \(AB:\) \(y = \left[ {4m - {{\left( {m + 1} \right)}^2}} \right]x + m\left( {m + 1} \right)\) có hệ số góc $k={4m - {{\left( {m + 1} \right)}^2}}$

Đường thẳng \(d:\,y = x - 9\) có hệ số góc $k=1$

\(\begin{array}{l}AB \bot d\\ \Leftrightarrow \left[ {4m - {{\left( {m + 1} \right)}^2}} \right].1 =  - 1\\ \Leftrightarrow 4m - {m^2} - 2m - 1 =  - 1\\ \Leftrightarrow  - {m^2} + 2m = 0\\ \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 2\end{array} \right.\end{array}\)