Phương trình lượng giác cơ bản

Phương trình $\sin x = m$ có nghiệm nếu $\left| m \right| \le 1$ và vô nghiệm nếu $\left| m \right| > 1$

Đáp án A: $|m|=|-3|=3>1$=> Loại

Đáp án B: $|m|=|-2|=2>1$=> Loại

Đáp án C: $|m|=|0|=0\le 1$ => Nhận

Đáp án D: $|m|=|3|=3>1$=> Loại

$\sin x = \sin \alpha  \Leftrightarrow \left[ \begin{array}{l}x = \alpha  + k2\pi \\x = \pi  - \alpha  + k2\pi \end{array} \right.\left( {k \in Z} \right)$

Ta có: $\sin x =  - 1 \Leftrightarrow \sin x = \sin \left( { - \dfrac{\pi }{2}} \right) \Leftrightarrow x =  - \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)$

Đáp án A: $\sin x =  - 1 \Leftrightarrow x =  - \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)$ nên A đúng.

Đáp án B: $\sin x = 0 \Leftrightarrow x = k\pi \left( {k \in Z} \right)$ nên B đúng, C sai.

Đáp án D: $\sin x = 1 \Leftrightarrow x = \dfrac{\pi }{2} + k2\pi \left( {k \in Z} \right)$ nên D đúng.

Bước 1:

Ta có: $\sin x = \dfrac{1}{2} \Leftrightarrow \sin x = \sin \dfrac{\pi }{6}$

Bước 2:

$\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in Z} \right)$

Bước 3:

+) Xét $x = \dfrac{\pi }{6} + k2\pi$

Ta có $- \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2} \Leftrightarrow - \dfrac{\pi }{2} \le \dfrac{\pi }{6} + k2\pi \le \dfrac{\pi }{2}$

$\begin{array}{l} - \dfrac{{2\pi }}{3} \le k2\pi  \le \dfrac{\pi }{3} \Leftrightarrow  - \dfrac{{2\pi }}{{3.2\pi }} \le k \le \dfrac{\pi }{{3.2\pi }}\\ \Leftrightarrow  - \dfrac{1}{3} \le k \le \dfrac{1}{6}\end{array}$

Mà $k \in \mathbb{Z} \Rightarrow k = 0$. Thay vào x ta được: $x = \dfrac{\pi }{6}$

+) Xét $x = \dfrac{{5\pi }}{6} + k2\pi$

$\begin{array}{l} - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2} \Leftrightarrow  - \dfrac{\pi }{2} \le \dfrac{{5\pi }}{6} + k2\pi  \le \dfrac{\pi }{2}\\ \Leftrightarrow  - \dfrac{{4\pi }}{3} \le k2\pi  \le  - \dfrac{\pi }{3} \Leftrightarrow  - \dfrac{{4\pi }}{{3.2\pi }} \le k \le  - \dfrac{\pi }{{3.2\pi }}\\ \Leftrightarrow  - \dfrac{2}{3} \le k \le  - \dfrac{1}{6}\end{array}$

Mà $k \in \mathbb{Z}$ nên không có giá trị k thỏa mãn

Vậy phương trình ban đầu có nghiệm duy nhất là $x = \dfrac{\pi }{6}$

Ta có:

$2\sin \left( {x + \dfrac{\pi }{4}} \right) - 2 = 0 \Leftrightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) = 1 \Leftrightarrow x + \dfrac{\pi }{4} = \dfrac{\pi }{2} + k2\pi  \Leftrightarrow x = \dfrac{\pi }{4} + k2\pi \left( {k \in Z} \right)$

Mà $\pi  \le x \le 5\pi  \Rightarrow \pi  \le \dfrac{\pi }{4} + k2\pi  \le 5\pi  \Leftrightarrow \dfrac{{3\pi }}{4} \le k2\pi  \le \dfrac{{19\pi }}{4} \Leftrightarrow \dfrac{3}{8} \le k \le \dfrac{{19}}{8} \Rightarrow k \in \left\{ {1;2} \right\}$

Vậy phương trình có hai nghiệm trong đoạn $\left[ {\pi ;5\pi } \right]$.

Bước 1:

$\sin x.\cos x = 0 \Leftrightarrow \dfrac{1}{2}\sin 2x = 0$

Bước 2:

$\Leftrightarrow \sin 2x = 0 \Leftrightarrow 2x = k\pi$ $\Leftrightarrow x = \dfrac{{k\pi }}{2}\left( {k \in \mathbb{Z}} \right)$

Ta có: $\cos 2x = 1 \Leftrightarrow \cos 2x = \cos 0 \Leftrightarrow 2x = k2\pi  \Leftrightarrow x = k\pi \left( {k \in Z} \right)$

Ta có:

+) $\cos x \ne 1 \Leftrightarrow x \ne k2\pi \left( {k \in Z} \right)$ nên A sai.

+) $\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi \left( {k \in Z} \right)$ nên B đúng, D sai.

+) $\cos x \ne  - 1 \Leftrightarrow x \ne \pi  + k2\pi \left( {k \in Z} \right)$ nên C sai.

Ta có: $2\cos x - 1 = 0 \Leftrightarrow \cos x = \dfrac{1}{2} \Leftrightarrow \cos x = \cos \dfrac{\pi }{3} \Leftrightarrow x =  \pm \dfrac{\pi }{3} + k2\pi \left( {k \in Z} \right)$

Ta có: $\sqrt 2 \cos \left( {x + \dfrac{\pi }{3}} \right) = 1$ $\Leftrightarrow \cos \left( {x + \dfrac{\pi }{3}} \right) = \dfrac{1}{{\sqrt 2 }} = \cos \dfrac{\pi }{4}$ $\Leftrightarrow \left[ \begin{array}{l}x + \dfrac{\pi }{3} = \dfrac{\pi }{4} + k2\pi \\x + \dfrac{\pi }{3} =  - \dfrac{\pi }{4} + k2\pi \end{array} \right.$ $\Leftrightarrow \left[ \begin{array}{l}x =  - \dfrac{\pi }{{12}} + k2\pi \\x =  - \dfrac{{7\pi }}{{12}} + k2\pi \end{array} \right.\left( {k \in Z} \right)$

Vì $0 \le x \le 2\pi$ nên $0 \le  - \dfrac{\pi }{{12}} + k2\pi  \le 2\pi$ $\Leftrightarrow \dfrac{\pi }{{12}} \le k2\pi  \le \dfrac{{25\pi }}{{12}}$ $\Leftrightarrow \dfrac{1}{{24}} \le k \le \dfrac{{25}}{{24}} \Rightarrow k = 1$

Và $0 \le  - \dfrac{{7\pi }}{{12}} + k2\pi  \le 2\pi$ $\Leftrightarrow \dfrac{{7\pi }}{{12}} \le k2\pi  \le \dfrac{{31\pi }}{{12}}$ $\Leftrightarrow \dfrac{7}{{24}} \le k \le \dfrac{{31}}{{24}} \Rightarrow k = 1$

Vậy có hai nghiệm của phương trình trong khoảng $\left[ {0;2\pi } \right]$.

Bước 1:

Ta có: $\cos 3x = \cos x \Leftrightarrow \left[ \begin{array}{l}3x = x + k2\pi \\3x =  - x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}2x = k2\pi \\4x = k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \dfrac{{k\pi }}{2}\end{array} \right.$

Bước 2:

+) Với họ nghiệm $x=k\pi$ ta có:

Khi $k=0$ thì $x=0$, điểm biểu diễn là điểm A (Vẫn là điểm đó khi k chẵn)

Khi $k=1$ thì $x=\pi$, điểm biểu diễn là A' (Vẫn là điểm đó khi k lẻ).

Như thế họ nghiệm $x=k\pi$ có $2$ điểm biểu diễn là $A,A'$.

+) Với họ nghiệm $x= \dfrac{{k\pi }}{2}$ ta có:

Khi $k=0$ thì $x=0$, điểm biểu diễn là điểm A (Vẫn là điểm đó khi k có dạng 4m, tức là k chia hết cho 4)

Khi $k=1$ thì $x= \dfrac{{\pi }}{2}$, điểm biểu diễn là B (Vẫn là điểm đó khi k có dạng 4m+1).

Khi $k=2$ thì $x= \pi$, điểm biểu diễn là A' (Vẫn là điểm đó khi k có dạng 4m+2).

Khi $k=3$ thì $x= \dfrac{{3\pi }}{2}$, điểm biểu diễn là B' (Vẫn là điểm đó khi k có dạng 4m+3).

Như thế họ nghiệm $x = \dfrac{{k\pi }}{2}$ có $4$ điểm biểu diễn là $A,A',B,B'$.

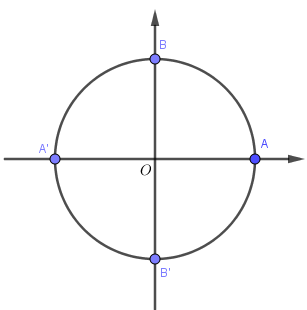
+) Kết hợp các điểm này lại ta được tổng cộng vẫn là 4 điểm $A,A',B,B'$. Mà 4 điểm này là 4 điểm biểu diễn của chính họ nghiệm $x = \dfrac{{k\pi }}{2}$ nên nghiệm của phương trình ban đầu là $x = \dfrac{{k\pi }}{2}$ $k \in Z$.

Bước 1:

${\sin ^2}x-\sin x = 0 \Leftrightarrow \left[ \begin{array}{l}\sin x = 0\\\sin x = 1\end{array} \right.$

Bước 2:

$\Leftrightarrow \left[ \begin{array}{l}x = k\pi \\x = \dfrac{\pi }{2} + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)$

Bước 3:

Xét $x = k\pi,k \in \mathbb{Z}$:

Vì $0 < x < \pi$ nên nghiệm của phương trình thỏa mãn:

$0 <  k\pi < \pi \Leftrightarrow 0<k<1$

Ta không thể tìm được số nguyên nào thỏa mãn điều trên

=> Không có số $k$ trong trường hợp này.

Xét $x = \dfrac{\pi }{2} + k2\pi,k \in \mathbb{Z}$:

Vì $0 < x < \pi$ nên nghiệm của phương trình thỏa mãn:

$0 <\dfrac{\pi }{2} + k2\pi<\pi \Leftrightarrow -\dfrac{\pi }{2} <k2\pi<\dfrac{\pi }{2}$

$\Leftrightarrow  - \dfrac{1}{4} < k < \dfrac{1}{4}$ mà $k \in \mathbb{Z} \Rightarrow k = 0$. Thay vào x ta được:

$x = \dfrac{\pi }{2} + 0 = \dfrac{\pi }{2}$

Vậy phương trình có 1 nghiệm duy nhất là $x= \dfrac{\pi }{2}$

Ta có:

$\sin 3x = \cos x \Leftrightarrow \sin 3x = \sin \left( {\dfrac{\pi }{2} - x} \right)$

$\Leftrightarrow \left[ \begin{array}{l}3x =\left( { \dfrac{\pi }{2} - x } \right)+ k2\pi \\3x = \pi  - \left( {\dfrac{\pi }{2} - x } \right)+ k2\pi \end{array} \right.$

$\Leftrightarrow \left[ \begin{array}{l}4x = \dfrac{\pi }{2} + k2\pi \\2x = \dfrac{\pi }{2} + k2\pi \end{array} \right.$

$\Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{2}\\x = \dfrac{\pi }{4} + k\pi \end{array} \right.\left( {k \in Z} \right)$

Ta có: $\sqrt 3 \tan x + 3 = 0 \Leftrightarrow \tan x =  - \sqrt 3  \Leftrightarrow x =  - \dfrac{\pi }{3} + k\pi \left( {k \in Z} \right)$

Bước 1:

Điều kiện:$\left\{ \begin{array}{l}\cos x \ne 0\\\cos \dfrac{x}{2} \ne 0\end{array} \right.$ $\Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{2} + k\pi \\\dfrac{x}{2} \ne \dfrac{\pi }{2} + k\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{2} + k\pi \\x \ne \pi  + k2\pi \end{array} \right.$

Bước 2:

Ta có: $\tan \dfrac{x}{2} = \tan x \Leftrightarrow \dfrac{x}{2} = x + k\pi$ $\Leftrightarrow  - \dfrac{x}{2} = k\pi \Leftrightarrow  - x = 2k\pi$ $\Leftrightarrow x =  - k2\pi \left( {k \in Z} \right)$ (*)

Đặt $k =  - l$ nên:

(*)$\Leftrightarrow x =  l2\pi \left( {l \in Z} \right)$ (TMĐK)

ĐKXĐ: $\sin \left( {5x - \dfrac{\pi }{8}} \right) \ne 0 \Leftrightarrow 5x - \dfrac{\pi }{8} \ne k\pi$ $\Leftrightarrow x \ne \dfrac{\pi }{{40}} + \dfrac{{k\pi }}{5}\left( {k \in Z} \right)$

Ta có:

$\sqrt 3 \cot \left( {5x - \dfrac{\pi }{8}} \right) = 0$ $\Leftrightarrow \cot \left( {5x - \dfrac{\pi }{8}} \right) = 0$ $\Leftrightarrow 5x - \dfrac{\pi }{8} = \dfrac{\pi }{2} + k\pi$ $\Leftrightarrow 5x = \dfrac{{5\pi }}{8} + k\pi$ $\Leftrightarrow x = \dfrac{\pi }{8} + \dfrac{{k\pi }}{5}\left( {k \in Z} \right)$

Điều kiện xác định: $\left\{ \begin{array}{l}\cos x \ne 0\\\sin x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{2} + k\pi \\x \ne k\pi \end{array} \right. \Leftrightarrow x \ne \dfrac{{k\pi }}{2} \Rightarrow D = R\backslash \left\{ {\dfrac{{k\pi }}{2},k \in Z} \right\}$

Do $\tan x.\cot x = 1,\forall x \in D$ nên tập nghiệm của phương trình là $R\backslash \left\{ {\dfrac{{k\pi }}{2},k \in Z} \right\}$ 

ĐKXĐ: $\left\{ \begin{array}{l}\cos 4x \ne 0\\\sin 2x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x \ne \dfrac{\pi }{2} + k\pi \\2x \ne k\pi \end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne \dfrac{\pi }{8} + \dfrac{{k\pi }}{4}\\x \ne \dfrac{{k\pi }}{2}\end{array} \right.$

Khi đó, dễ thấy $\cot 2x \ne 0$ (Nếu $\cot 2x = 0$ thì phương trình thành 0=1 =>Vô nghiệm) nên phương trình tương đương:

$\tan 4x.\cot 2x = 1 \Leftrightarrow \tan 4x = \dfrac{1}{{\cot 2x}} \\ \Leftrightarrow \tan 4x = \tan 2x \Leftrightarrow 4x = 2x + k\pi  \\ \Leftrightarrow x = \dfrac{{k\pi }}{2}$

Kết hợp với điều kiện ta được phương trình vô nghiệm.

Bước 1:

Ta có: $\tan \left( {\dfrac{\pi }{2} - x} \right) + 2\tan \left( {2x + \dfrac{\pi }{2}} \right) = 1$$\Leftrightarrow \cot x - 2\cot 2x = 1$

ĐK: $\left\{ \begin{array}{l}\sin x \ne 0\\\sin 2x \ne 0\end{array} \right. \Leftrightarrow \sin 2x \ne 0 \Leftrightarrow x \ne \dfrac{{k\pi }}{2}$

Bước 2:

Khi đó phương trình tương đương:

$\begin{array}{l}\cot x - 2\cot 2x = 1 \\ \Leftrightarrow \cot x - 2.\dfrac{{1 - {{\tan }^2}x}}{{2\tan x}} = 1 \\ \Leftrightarrow \cot x - \dfrac{{\tan x.\cot x - {{\tan }^2}x}}{{\tan x}} = 1\\ \Leftrightarrow \cot x - \left( {\cot x - \tan x} \right) = 1 \Leftrightarrow \tan x = 1 \Leftrightarrow x = \dfrac{\pi }{4} + k\pi \left( {k \in Z} \right)\left( {TMDK} \right)\end{array}$