Cho hàm số $y = f\left( x \right)$ có đạo hàm trên $\left( {a;b} \right)$. Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thuộc \((a;b)\) thì
Nếu $f'\left( x \right)$ đổi dấu từ âm sang dương qua điểm ${x_0}$ thì ${x_0}$ là điểm cực tiểu của hàm số.
Giả sử $y = f\left( x \right)$ có đạo hàm cấp hai trên $\left( {a;b} \right)$. Nếu $\left\{ \begin{gathered}f'\left( {{x_0}} \right) = 0 \hfill \\ f''\left( {{x_0}} \right) > 0 \hfill \\ \end{gathered} \right.$ thì
Nếu $\left\{ \begin{gathered} f'\left( {{x_0}} \right) = 0 \hfill \\ f''\left( {{x_0}} \right) > 0 \hfill \\\end{gathered} \right.$ thì ${x_0}$ là một điểm cực tiểu của hàm số.
Cho các phát biểu sau:
1. Hàm số $y = f\left( x \right)$ đạt cực đại tại ${x_0}$ khi và chỉ khi đạo hàm đổi dấu từ dương sang âm qua ${x_0}$.
2. Hàm số $y = f\left( x \right)$ đạt cực trị tại ${x_0}$ khi và chỉ khi ${x_0}$ là nghiệm của đạo hàm.
3. Nếu $f'\left( {{x_0}} \right) = 0$ và $f''\left( {{x_0}} \right) = 0$ thì ${x_0}$ không phải là cực trị của hàm số $y = f\left( x \right)$ đã cho.
4. Nếu $f'\left( {{x_0}} \right) = 0$ và $f''\left( {{x_o}} \right) > 0$ thì hàm số đạt cực đại tại ${x_0}$.
Các phát biểu đúng là:
+) Ta có định lí: Nếu $f'\left( x \right)$ đổi dấu từ dương sang âm khi $x$ qua điểm ${x_o}$ (theo chiều tăng) thì hàm số đạt cực đại tại điểm ${x_o}$ $ \Rightarrow $ 1 đúng.
+) Điều kiện cần để ${x_o}$ là điểm cực trị của hàm số là: ${x_o}$ là nghiệm của phương trình $f'\left( x \right) = 0$$ \Rightarrow $ 2 sai.
+) Nếu $f'\left( {{x_o}} \right) = 0$ và $f\left( x \right)$ có đạo hàm cấp hai khác 0 tại điểm ${x_o}$ thì:
-) Nếu $f''\left( {{x_o}} \right) < 0$ thì hàm số $f\left( x \right)$ đạt cực đại tại điểm ${x_o}$.
-) Nếu $f''\left( {{x_o}} \right) > 0$ thì hàm số $f\left( x \right)$ đạt cực tiểu tại điểm ${x_o}$.
+) Nếu $f'\left( {{x_o}} \right) = 0$ và $f''\left( {{x_o}} \right) = 0$ thì ta không kết luận gì chứ không phải hàm số không đạt cực trị tại ${x_0}$.
Khi \(\left\{ \begin{array}{l}f'\left( {{x_0}} \right) = 0\\f''\left( {{x_0}} \right) = 0\end{array} \right.\) thì ta không kết luận gì vì có thể xảy ra cả hai trường hợp là hàm số đạt cực trị hoặc không đạt cực trị tại \({x_0}\).
Ví dụ:
+) TH1: Xét hàm \(f\left( x \right) = {x^4}\) có \(f'\left( x \right) = 4{x^3} = 0 \Leftrightarrow x = 0\)
\(f''\left( x \right) = 12{x^2}\) và \(f''\left( 0 \right) = 0\).
Trong TH này hàm số có \(f''\left( 0 \right) = 0\) nhưng vẫn đạt cực tiểu tại \(x = 0\) vì đạo hàm \(f'\left( x \right)\) đổi dấu từ âm sang dương qua \(x = 0\).
+) TH2: Xét hàm \(g\left( x \right) = {x^3}\) có \(f'\left( x \right) = 3{x^2} = 0 \Leftrightarrow x = 0\)
\(f''\left( x \right) = 6x \Rightarrow f''\left( 0 \right) = 0\)
Trong TH này hàm số có \(f''\left( 0 \right) = 0\) nhưng không đạt cực trị tại \(x = 0\) vì đạo hàm \(f'\left( x \right) = 3{x^2}\) không đổi dấu của \(x = 0\).
$ \Rightarrow $ 3 và 4 sai.
Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ có:
Điều kiện để hàm số bậc ba không có cực trị là phương trình $y' = 0$ vô nghiệm hoặc có nghiệm kép.
Số điểm cực trị của đồ thị hàm số $y = \dfrac{{x - 1}}{{2 - x}}$ là:
TXĐ: $D = R\backslash \left\{ 2 \right\}$
Dễ thấy $y' = \dfrac{1}{{{{\left( {2 - x} \right)}^2}}} > 0$ $\forall x \in D$
$ \Rightarrow $ Hàm số đồng biến trên các khoảng $\left( -\infty ;2 \right)$ và $\left( 2;+\infty \right)$
$ \Rightarrow $ Hàm số không có cực trị.
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số $y = {x^3} - 3{x^2} + 1$ là:
Cách 1:
$y' = 3{x^2} - 6x$ ;
$y' = 0 \Leftrightarrow 3x\left( {x - 2} \right) = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \Rightarrow y = 1 \hfill \\x = 2 \Rightarrow y = - 3 \hfill \\ \end{gathered} \right.$
Từ đây suy ra hai điểm cực trị có tọa độ $A\left( {0,1} \right)$ và $B\left( {2, - 3} \right).$
Phương trình đường thẳng qua hai điểm $A, B$ là: $\dfrac{{x - 0}}{{2 - 0}} = \dfrac{{y - 1}}{{ - 3 - 1}}$ $\Leftrightarrow - 4x = 2\left( {y - 1} \right) \Leftrightarrow y = - 2x + 1.$
Cách 2:
Ta có $y' = 3{x^2} - 6x$
Khi đó ${x^3} - 3{x^2} + 1 $ $= \left( {3{x^2} - 6x} \right)\left( {\dfrac{1}{3}x - \dfrac{1}{3}} \right) - 2x + 1$
Vậy đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là $y = - 2x + 1$
Cách 3:
Bước 1:
$y'=3x^2-6x$; $y''=6x-6$
Bước 2:
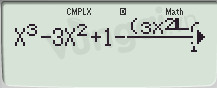
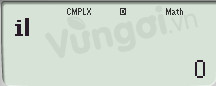
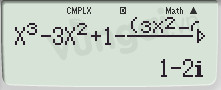
Bước 3: Ta được a=1 và b=-2
Vậy đường thẳng là: $y=-2x+1$
Hàm số nào sau đây không có cực trị?
Đáp án A: $y' = 3{x^2} \ge 0 $ với mọi \(x\) nên hàm số đồng biến trên \(R\). Do đó nó không có cực trị.
Vậy hàm số $y = {x^3}$ không có cực trị.
Đáp án B: $y' = 3{x^2} + 6x = 3x\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \hfill\\x = - 2 \hfill \\ \end{gathered} \right.$ $y'' = 6x + 6 \Rightarrow \left\{ \begin{gathered} y''\left( 0\right) = 6 > 0 \hfill \\ y''\left( { - 2} \right) = - 6 < 0 \hfill \\ \end{gathered} \right.$, do đó $x = 0$ là điểm cực tiểu của hàm số, $x = - 2$ là điểm cực đại của hàm số.
Đáp án C: $y' = 4{x^3} = 0 \Leftrightarrow x = 0 \Rightarrow \left\{ \begin{gathered} y' > 0,\forall x > 0\hfill \\ y' < 0,\forall x < 0 \hfill \\ \end{gathered} \right. \Rightarrow x = 0$ là điểm cực tiểu của hàm số.
Đáp án D: $y' = 4{x^3} = 0 \Leftrightarrow x = 0 \Rightarrow \left\{ \begin{gathered}y' > 0,\forall x > 0 \hfill \\ y' < 0,\forall x < 0 \hfill \\ \end{gathered} \right. \Rightarrow x = 0$ là điểm cực tiểu của hàm số.
Hàm số $f\left( x \right) = 2\sin 2x - 3$ đạt cực tiểu tại:
Ta có: $f\left( x \right) = 2\sin 2x - 3$
TXĐ: $D = R.$
$f'\left( x \right) = 4\cos 2x$, $f'\left( x \right) = 0 \Leftrightarrow \cos 2x = 0 \Leftrightarrow 2x =\dfrac{\pi }{2} + k\pi $ $\Leftrightarrow x = \dfrac{\pi }{4} + \dfrac{{k\pi }}{2}$, $k \in Z$
$f''\left( x \right) = - 8\sin 2x$
Ta có: $f''\left( {\dfrac{\pi }{4} + \dfrac{{k\pi }}{2}} \right) = - 8\sin \left( {\dfrac{\pi }{2} + k\pi } \right) $ , $k \in Z$
Khi $k=2n$ thì \(\sin \left( {\dfrac{\pi }{2} + 2n\pi } \right) = \sin \dfrac{\pi }{2} = 1\) nên \(f''\left( {\dfrac{\pi }{4} + \dfrac{{2n\pi }}{2}} \right) = - 8 < 0\)
Khi $k=2n+1$ thì \(\sin \left( {\dfrac{\pi }{2} + \left( {2n + 1} \right)\pi } \right) = \sin \dfrac{{3\pi }}{2} = - 1\) nên \(f''\left( {\dfrac{\pi }{4} + \dfrac{{\left( {2n + 1} \right)\pi }}{2}} \right) = 8 > 0\)
Vậy hàm số đạt cực tiểu tại $x = \dfrac{\pi }{4} + \dfrac{\left( {2k + 1}\right)\pi }{2} $
Đồ thị hàm số nào sau đây có $3$ điểm cực trị?
Xét phương án B ta thấy $y' =4x^3-4x=4x(x^2-1)= 4x\left( {x + 1} \right)\left( {x - 1} \right).$
Phương trình $y' = 0$ có ba nghiệm đơn phân biệt cho nên thỏa mãn yêu cầu bài toán.
Ngoài ra, ta tính $y'$ và giải các phương trình $y'=0$ ở từng đáp án ta thấy:
Đáp án A: $y'=4x^3+4x=4x(x^2+1)$ chỉ có $1$ nghiệm $x=0$ nên loại.
Đáp án C: $y'=8x^3+8x=8x(x^2+1)$ chỉ có $1$ nghiệm $x=0$ nên loại.
Đáp án D: $y'=-4x^3-4x=-4x(x^2+1)$ chỉ có $1$ nghiệm $x=0$ nên loại.
Cho hàm số $y = f\left( x \right)$ có đạo hàm $f'\left( x \right) = \left( {x -1}\right)\left({{x^2}- 2} \right)\left( {{x^4} - 4} \right)$. Số điểm cực trị của hàm số $y = f\left( x \right)$ là:
Ta có: $f'\left( x \right) = 0$
$\begin{gathered} \Leftrightarrow \left( {x - 1} \right)\left( {{x^2} - 2}\right)\left( {{x^4} - 4} \right) = 0 \hfill \\\Leftrightarrow \left( {x - 1} \right){\left( {{x^2} - 2}\right)^2}\left( {{x^2} + 2} \right) = 0 \hfill \\ \Leftrightarrow \left[ \begin{gathered}x = 1 \hfill \\ x = \sqrt 2 \hfill \\x = - \sqrt { 2} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $
Một điểm được gọi là cực trị của hàm số khi đạo hàm của hàm số đổi dấu qua điểm đó.
Ta nhận thấy đạo hàm của hàm số chỉ đổi dấu qua $x = 1$ và không đổi dấu qua $x = \pm \sqrt 2 $.
Vậy hàm số có $1$ điểm cực trị.
Đồ thị hàm số $y = {x^3} - 3x + 2$ có $2$ điểm cực trị $A,\;B.$ Diện tích tam giác $OAB\;$ với $O(0;0)$ là gốc tọa độ bằng:
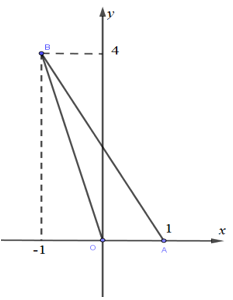
$\begin{array}{*{20}{l}}{y = {x^3} - 3x + 2 \Rightarrow y' = 3{x^2} - 3}\\{y' = 0 \Leftrightarrow x = {\rm{\;}} \pm 1}\end{array}$
Tọa độ $2$ điểm cực trị : $A(1;{\mkern 1mu} 0),{\mkern 1mu} {\mkern 1mu} B( - 1;4)$
Khi đó ${S_{\Delta OAB}} = \dfrac{1}{2}.OA.{d(B,OA)} = \dfrac{1}{2}.\left| {{x_A}} \right|.\left| {{y_B}} \right| = \dfrac{1}{2}.\left| 1 \right|.\left| 4 \right| = 2$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên trên khoảng $\left( {0;2} \right)$ như sau:
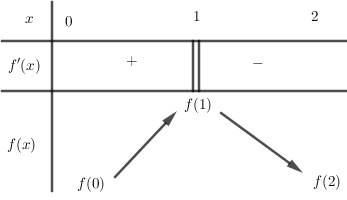
Khẳng định nào sau đây là khẳng định đúng:
A sai vì trên đoạn $\left( {0;2} \right)$ vẫn có cực trị tại $x = 1$.
Hàm số đạt cực đại tại $x=1$ nên B đúng.
C sai vì hàm số đạt cực đại tại $x = 1$ không phải cực tiểu
D sai vì đạo hàm không đổi dấu qua $x = 0$
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
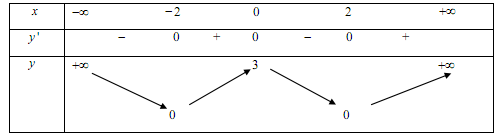
Khẳng định nào sau đây là khẳng định sai:
Từ bảng biến thiên ta thấy:
- Đạo hàm đổi dấu từ âm sang dương qua $x = - 2$ nên $x = - 2$ là điểm cực tiểu của hàm số (C đúng).
- Đạo hàm đổi dấu từ âm sang dương qua $x = 2$ nên $x = 2$ là điểm cực tiểu của hàm số (A đúng).
- Đạo hàm đổi dấu từ dương sang âm qua $x = 0$ nên $x = 0$ là điểm cực đại của hàm số (D đúng).
- Qua điểm $x = 3$ thì đạo hàm không đổi dấu nên $x = 3$ không là điểm cực trị của hàm số (B sai).
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau. Khẳng định nào dưới đây là đúng?
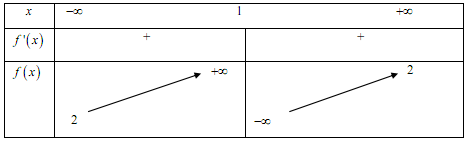
Từ bảng biến thiên ta thấy, đạo hàm không đổi dấu trên $\left( { - \infty ; + \infty } \right)$ nên hàm số không có cực trị.
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như hình bên dưới, chọn khẳng định sai:
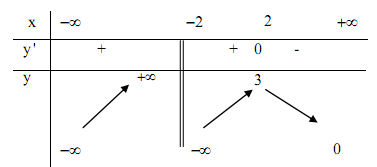
Từ bảng biến thiên ta thấy:
Đạo hàm đổi dấu từ dương sang âm qua điểm $x = 2$ nên $x = 2$ là điểm cực đại của hàm số, $y = 3$ là giá trị cực đại của hàm số và $\left( {2;3} \right)$ là điểm cực đại của đồ thị hàm số.
Ngoài ra, đạo hàm không đổi dấu qua điểm $x = - 2$ nên $x = - 2$ không là điểm cực trị của hàm số.
Hàm số $y = {x^3} - 3x^2 + 4$ đạt cực tiểu tại:
TXĐ: $D=R$
Ta có: $y' = 3{x^2} - 6x$
$ \Rightarrow y' = 0 \Leftrightarrow x = 0$ hoặc $x = 2$
Ta có bảng biến thiên:
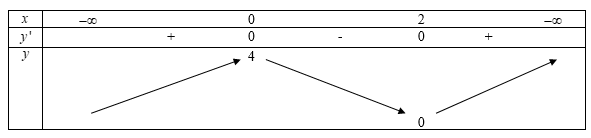
Từ bảng dễ thấy hàm số đạt giá trị cực tiểu $y = 0$ tại $x = 2$
Cho hàm số $y = \dfrac{{ - {x^2} + 3x + 6}}{{x + 2}}$, chọn kết luận đúng:
Đồ thị hàm số có điểm cực tiểu $\left( { - 4;11} \right)$ và điểm cực đại $\left( {0;3} \right)$.
Ta có: $y = \dfrac{{ - {x^2} + 3x + 6}}{{x + 2}} = - x + 5 - \dfrac{4}{{x + 2}}$.
TXĐ: $D = R\backslash \left\{ { - 2} \right\}$.
Ta có: $y' = - 1 + \dfrac{4}{{{{\left( {x + 2} \right)}^2}}} = \dfrac{{ - {x^2} - 4x}}{{{{\left( {x + 2} \right)}^2}}};y' = 0 \Leftrightarrow \left[ \begin{gathered}x = 0 \Rightarrow y = 3 \hfill \\ x = - 4 \Rightarrow y = 11 \hfill \\ \end{gathered} \right.$
Bảng biến thiên:
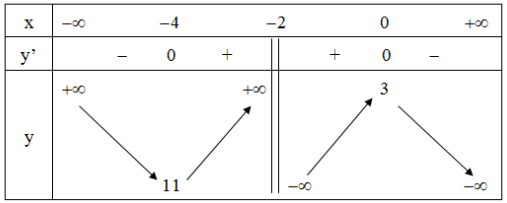
Từ bảng biến thiên ta thấy đồ thị hàm số có điểm cực đại là $\left( {0;3} \right)$ và điểm cực tiểu là $\left( { - 4;11} \right)$.
Cho hàm số bậc hai $y = f\left( x \right)$ có đồ thị như hình vẽ bên, một hàm số $g\left( x \right)$ xác định theo $f\left( x \right)$ có đạo hàm $g'\left( x \right) = f\left( x \right) + m$. Tìm tất cả các giá trị thực của tham số $m$ để hàm số $g\left( x \right)$ không có cực trị.
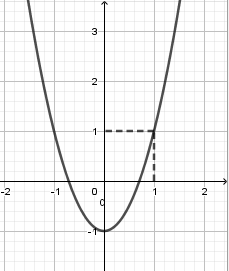
Gọi hàm số $y = f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right)$.
Đồ thị hàm số $y = a{x^2} + bx + c$ nhận điểm $\left( {0; - 1} \right)$ làm đỉnh và đi qua điểm $\left( {1;1}\right)$ nên $a = 2;b = 0;c = - 1$ hay $f\left( x \right) = 2{x^2} - 1$.
Do đó $g'\left( x \right) = 2{x^2} + m - 1$.
Hàm số $y = g\left( x \right)$ không có cực trị$ \Leftrightarrow g'\left( x \right) = 0$ vô nghiệm hoặc có nghiệm kép.
$ \Leftrightarrow m - 1 \geqslant 0 \Leftrightarrow m \geqslant 1$.
Vậy $m \geqslant 1$.
Điểm thuộc đường thẳng \(d:x-y-1=0\) cách đều hai điểm cực trị của đồ thị hàm số \(y={{x}^{3}}-3{{x}^{2}}+2\) là
Ta có \(y={{x}^{3}}-3{{x}^{2}}+2\,\,\xrightarrow{{}}\,\,{y}'=3{{x}^{2}}-6x;\,\,{y}'=0\Leftrightarrow \left[\begin{align} x=0\,\,\Rightarrow \,\,y\left( 0 \right)=2 \\ x=2\,\,\Rightarrow \,\,y\left( 2 \right)=-\,2 \\ \end{align} \right..\)
Suy ra tọa độ hai điểm cực trị của đồ thị hàm số là \(A\left( 0;2 \right),\,\,B\left( 2;-\,2 \right).\)
Gọi \(M\in d\Rightarrow M\left( a;a-1 \right),\) khi đó \(\left\{ \begin{align} MA=\sqrt{{{a}^{2}}+{{\left( a-3 \right)}^{2}}} \\ MB=\sqrt{{{\left( a-2 \right)}^{2}}+{{\left( a+1 \right)}^{2}}} \\ \end{align} \right.\)
Mà \(M\) cách đều \(A,\,\,B\)
Suy ra \(M{{A}^{2}}=M{{B}^{2}}\)\(\Leftrightarrow \)\({{a}^{2}}+{{\left( a-3 \right)}^{2}}={{\left( a-2 \right)}^{2}}+{{\left( a+1 \right)}^{2}}\)\(\Leftrightarrow \)\(a=1\,\,\Rightarrow \,\,M\left( 1;0 \right).\)
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên.
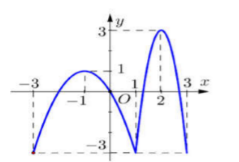
Trên đoạn \(\left[ { - 3;\,3} \right],\) hàm số đã cho có mấy điểm cực trị?
Dựa vào đồ thị hàm số ta thầy, trên đoạn \(\left[ { - 3;\,\,3} \right],\) hàm số \(y = f\left( x \right)\) có 3 điểm cực trị là \(\left( { - 1;\,\,1} \right);\,\,\,\left( {1; - 3} \right);\,\,\left( {2;\,\,3} \right).\)

