Hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) xác định trên:
Hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) xác định trên \(\left( {0; + \infty } \right)\).
Hàm số \(y = {\log _a}x\) có đạo hàm là:
Điều kiện xác định: $x>0$
Đạo hàm hàm số \(y = {\log _a}x\) là \(y' = \dfrac{1}{{x\ln a}}\)
Chọn mệnh đề đúng:
Giới hạn cần nhớ: \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\)
Cho hàm số \(y = {\log _a}x\). Nếu \(0 < a < 1\) thì hàm số:
Hàm số \(y = {\log _a}x\) nghịch biến trên \(\left( {0; + \infty } \right)\) nếu \(0 < a < 1\) và đồng biến trên \(\left( {0; + \infty } \right)\) nếu \(a > 1\).
Tiệm cận đứng của đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) là đường thẳng:
Đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đường tiệm cận đứng là \(x = 0\) (trục \(Oy\))
Điểm \(\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) nếu:
Điểm \(\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) nếu \({y_0} = {\log _a}{x_0}\).
Điểm nào sau đây không thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\)?
- Đồ thị hàm số luôn đi qua các điểm \(\left( {1;0} \right)\) và \(\left( {a;1} \right)\).
- Với \(x = {a^2}\) thì \(y = {\log _a}x = {\log _a}{a^2} = 2\) nên đồ thị hàm số đi qua \(\left( {{a^2};2} \right)\) nên C sai, D đúng.
Cho hàm số \(y = {\log _{\frac{\pi }{4}}}x\). Khẳng định nào sau đây sai?
- Hàm số \(y = {\log _{\frac{\pi }{4}}}x\) có tập xác định \(D = \left( {0; + \infty } \right)\).
- Vì \(0 < \dfrac{\pi }{4} < 1\) nên hàm số nghịch biến trên TXĐ
- Tiệm cận đứng của đồ thị hàm số là trục $Oy$
- Đồ thị hàm số nằm hoàn toàn bên phải trục hoành (vì \(x > 0\))
Trong các khẳng định sau, khẳng định nào đúng?
\(\log a + \log b = \log \left( {ab} \right)\) nên ý A sai
Nhận thấy \({a^{x + y}} = {a^x}.{a^y}\) nên mệnh đề ở ý B sai.
Vì $12 > 1$ nên \(y = {\log _{12}}x\) là hàm đồng biến trên khoảng $(0; + \infty )$ nên D sai
Cho $a, b$ là các số thực, thỏa mãn \(0 < a < 1 < b\), khẳng định nào sau đây là đúng?
Ta có: \(0 < a < 1\) nên hàm số \(y = {\log _a}x\) nghịch biến, do đó \(b > 1\) nên \({\log _a}b < {\log _a}1 = 0\).
Vì \(b > 1\) nên hàm số \(y = {\log _b}x\) đồng biến, do đó \(a < 1\) nên \({\log _b}a < {\log _b}1 = 0\).
Vậy \({\log _a}b < 0;{\log _b}a < 0 \Rightarrow {\log _a}b + {\log _b}a < 0\).
Tìm tập xác định D của hàm số \(y = {\log _{\sqrt 2 }}\left( {\dfrac{{ - 3}}{{2 - 2x}}} \right)\).
Điều kiện : \(\dfrac{{ - 3}}{{2 - 2x}} > 0 \Leftrightarrow 2 - 2x < 0 \Leftrightarrow x > 1.\)
Đạo hàm hàm số \(y = {\log _{2018}}\left( {2018x + 1} \right)\) là:
Ta có: \(\left[ {{{\log }_{2018}}\left( {2018x + 1} \right)} \right]' = \dfrac{{\left( {2018x + 1} \right)'}}{{\left( {2018x + 1} \right)\ln 2018}} = \dfrac{{2018}}{{\left( {2018x + 1} \right)\ln 2018}}\)
Tính đạo hàm hàm số \(y = \ln \left( {1 + \sqrt {x + 1} } \right)\).
Ta có: \(y' = \left[ {\ln \left( {1 + \sqrt {x + 1} } \right)} \right]' = \dfrac{{\left( {1 + \sqrt {x + 1} } \right)'}}{{1 + \sqrt {x + 1} }} = \dfrac{{\dfrac{1}{{2\sqrt {x + 1} }}}}{{1 + \sqrt {x + 1} }} = \dfrac{1}{{2\sqrt {x + 1} \left( {1 + \sqrt {x + 1} } \right)}}\)
Cho $a, b$ là các số thực dương, thỏa mãn \({a^{\frac{3}{4}}} > {a^{\frac{4}{5}}}\) và \({\log _b}\dfrac{1}{2} < {\log _b}\dfrac{2}{3}\). Mệnh đề nào dưới đây đúng?
Ta có:
\(\dfrac{3}{4} < \dfrac{4}{5}\) và \({a^{\frac{3}{4}}} > {a^{\frac{4}{5}}}\)\( \Rightarrow 0 < a < 1\)
\(\dfrac{1}{2} < \dfrac{2}{3}\) và \({\log _b}\dfrac{1}{2} < {\log _b}\dfrac{2}{3}\)\( \Rightarrow b > 1\)
Nếu gọi \(({G_1})\) là đồ thị hàm số \(y = {a^x}\) và \(({G_2})\)là đồ thị hàm số \(y = {\log _a}x\) với \(0 < a \ne 1\). Mệnh đề nào dưới đây đúng ?
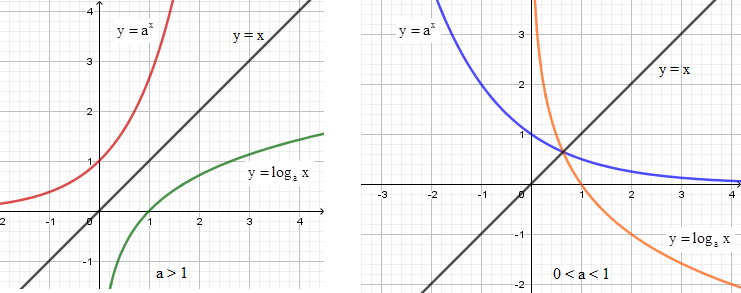
Quan sát hình vẽ ta thấy hai đồ thị hàm số đối xứng nhau qua đường thẳng \(y = x\).
Cho ba số thực dương $a, b, c$ khác $1$. Đồ thị các hàm số $y = \log_{a} x, y=\log_{b} x, y= \log_{c} x$ được cho trong hình vẽ sau:
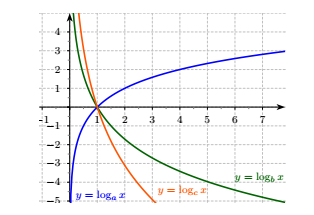
Mệnh đề nào dưới đây đúng?
Quan sát hình vẽ ta thấy:
- Hàm số \(y = {\log _a}x\) là hàm đồng biến nên ta có \(a > 1\) .
- Hai hàm số \(y = {\log _b}x,y = {\log _c}x\) nghịch biến nên có \(0 < b,c < 1\)
Từ nhận xét này ta thấy \(a\) là số lớn nhất.
Tìm tất cả các giá trị thực của tham số $m$ sao cho hàm số \(y = \log ({x^2} - 2mx + 4)\) có tập xác định là $R$
Giải điều kiện: \({x^2} - 2mx + 4 > 0,\forall x \in R\)
\(\Delta ' = {m^2} - 4 < 0 \Leftrightarrow (m - 2)(m + 2) < 0\). Suy ra \( - 2 < m < 2\)
Tìm tập giá trị \({\rm{T}}\) của hàm số \(f\left( x \right) = \dfrac{{\ln x}}{x}\) với \(x \in \left[ {1;{e^2}} \right].\)
Hàm số \(f\left( x \right)\) xác định và liên tục trên đoạn \(\left[ {1;{e^2}} \right]\).
Đạo hàm \(f'\left( x \right) = \dfrac{{1 - \ln x}}{{{x^2}}}\)\( \Rightarrow f'\left( x \right) = 0 \Leftrightarrow 1 - \ln x = 0\) \( \Leftrightarrow x = e \in \left[ {1;{e^2}} \right]\)
Ta có \(\left\{ \begin{array}{l}f\left( 1 \right) = 0\\f\left( e \right) = \dfrac{1}{e}\\f\left( {{e^2}} \right) = \dfrac{2}{{{e^2}}}\end{array} \right.\) \( \Rightarrow \mathop {\min }\limits_{x \in \left[ {1;{e^2}} \right]} f\left( x \right) = 0,\mathop {\max }\limits_{x \in \left[ {1;{e^2}} \right]} f\left( x \right) = \dfrac{1}{e}\) \( \Rightarrow {\rm{T}} = \left[ {0;\dfrac{1}{e}} \right]\)
Biết hai hàm số $y = {a^x}$ và $y = f\left( x \right)$ có đồ thị như hình vẽ đồng thời đồ thị của hai hàm số này đối xứng nhau qua đường thẳng $d:y = - x$. Tính $f\left( { - {a^3}} \right).$
Giả sử \(M\left( {{x_M};{y_M}} \right)\) là điểm thuộc hàm số \(y = {a^x}\); \(N\left( {{x_0};{y_0}} \right)\) là điểm đối xứng của \(M\) qua đường thẳng \(y = - x\).
Gọi \(I\) là trung điểm của \(MN \Rightarrow I\left( {\dfrac{{{x_M} + {x_0}}}{2};\dfrac{{{y_M} + {y_0}}}{2}} \right)\).
Vì \(M,{\rm{ }}N\) đối xứng nhau qua $d$ $ \Rightarrow \left\{ \begin{array}{l}I \in d\\\overrightarrow {MN} //\overrightarrow {{n_d}} \end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\dfrac{{{y_M} + {y_0}}}{2} = - \dfrac{{{x_M} + {x_0}}}{2}\\\dfrac{{{x_M} - {x_0}}}{1} = \dfrac{{{y_M} - {y_0}}}{1}\end{array} \right.$ $ \Leftrightarrow \left\{ \begin{array}{l}{x_0} = - {y_M}\\{y_0} = - {x_M}\end{array} \right.$
Ta có \(M\left( {{x_M};{y_M}} \right) \in \) đồ thị \(y = {a^x}\) nên \({y_M} = {a^{{x_M}}}\).
Do đó ${x_0} = - {y_M} = - {a^{{x_M}}} = - {a^{ - {y_0}}}$$ \Rightarrow - {y_0} = {\log _a}\left( { - {x_0}} \right) \Leftrightarrow {y_0} = - {\log _a}\left( { - {x_0}} \right)$.
Điều này chứng tỏ điểm \(N\) thuộc đồ thị hàm số $f\left( x \right) = - {\log _a}\left( { - x} \right)$.
Khi đó \(f\left( { - {a^3}} \right) = - {\log _a}{a^3} = - 3.\)
Tìm tham số \(m\) để hàm số \(y = \dfrac{{{{\log }_{\dfrac{1}{2}}}x - 2}}{{{{\log }_2}x - m}}\) đồng biến trên khoảng \(\left( {0;1} \right)\).
Ta có: \(y = \dfrac{{{{\log }_{\dfrac{1}{2}}}x - 2}}{{{{\log }_2}x - m}} = \dfrac{{ - {{\log }_2}x - 2}}{{{{\log }_2}x - m}}\).
Đặt \(t = {\log _2}x\), với \(x \in \left( {0;1} \right) \Rightarrow t \in \left( { - \infty ;0} \right)\).
\( \Rightarrow \) Hàm số \(y = \dfrac{{{{\log }_{\dfrac{1}{2}}}x - 2}}{{{{\log }_2}x - m}}\) đồng biến trên khoảng \(\left( {0;1} \right)\) khi và chỉ khi \(y = f\left( t \right) = \dfrac{{ - t - 2}}{{t - m}}\) đồng biến trên \(\left( { - \infty ;0} \right)\).
\( \Leftrightarrow \left\{ \begin{array}{l}y' = \dfrac{{m + 2}}{{{{\left( {t - m} \right)}^2}}} > 0\\m \notin \left( { - \infty ;0} \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m > - 2\\m \ge 0\end{array} \right. \Leftrightarrow m \ge 0\).
