Giới hạn của hàm số

Ta có

$\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {4{x^2} - 3x + 1}  - \left( {ax + b} \right)} \right) = 0$$ \Leftrightarrow \mathop {\lim }\limits_{x \to  + \infty } \left( {\left( {\sqrt {4{x^2} - 3x + 1}  - ax} \right) - b} \right) = 0$$ \Leftrightarrow \mathop {\lim }\limits_{x \to  + \infty } \left( {\dfrac{{4{x^2} - 3x + 1 - {a^2}{x^2}}}{{\sqrt {4{x^2} - 3x + 1}  + ax}} - b} \right) = 0$$ \Leftrightarrow \mathop {\lim }\limits_{x \to  + \infty } \left( {\dfrac{{\left( {4 - {a^2}} \right){x^2} - 3x + 1}}{{\sqrt {4{x^2} - 3x + 1}  + ax}} - b} \right) = 0$

$ \Leftrightarrow \left\{ \begin{array}{l}4 - {a^2} = 0\\a > 0\\\dfrac{{ - 3}}{{2 + a}} - b = 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b =  - \dfrac{3}{4}\end{array} \right.$.

Vậy $a - 4b = 5$.

Hàm số \(y = f\left( x \right)\) có giới hạn là số \(L\) khi \(x\) dần tới \({x_0}\) kí hiệu là \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L\).

Ta có \(\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {a{x^2} + bx}  - cx} \right) =  - 2\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{\left( {a - {c^2}} \right){x^2} + bx}}{{\sqrt {a{x^2} + bx}  + cx}} =  - 2\).

Điều này xảy ra \( \Leftrightarrow \left\{ \begin{array}{l}a - {c^2} = 0\,\,\,\,\left( {a,\,\,c > 0} \right)\\\dfrac{b}{{\sqrt a  + c}} =  - 2\end{array} \right.\) . (Vì nếu \(c \le 0\) thì \(\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {a{x^2} + bx}  - cx} \right) =  + \infty \)).

Mặt khác, ta cũng có \({c^2} + a = 18\).

Do đó, \(\left\{ \begin{array}{l} a = {c^2} = 9\\b =  - 2\left( {\sqrt a  + c} \right)\end{array} \right.\) \( \Leftrightarrow \) \(a = 9\), \(b =  - 12\), \(c = 3\). Vậy \(P = a + b + 5c\)\( = 12\).

\(\mathop {\lim }\limits_{x \to 3} \sqrt {\dfrac{{9{x^2} - x}}{{\left( {2x - 1} \right)\left( {{x^4} - 3} \right)}}}  \)

\(= \sqrt {\dfrac{{{{9.3}^2} - 3}}{{\left( {2.3 - 1} \right)\left( {{3^4} - 3} \right)}}}  = \dfrac{1}{{\sqrt 5 }} = \dfrac{{\sqrt 5 }}{5}\)

Vì hàm số có giới hạn hữu hạn tại $x = 1$ nên biểu thức tử nhận $x = 1$ làm nghiệm, hay $1 + a + b = 0$.

Áp dụng vào giả thiết, được $\mathop {\lim }\limits_{x \to 1} \dfrac{{{x^2} + ax - 1 - a}}{{{x^2} - 1}} = \dfrac{{ - 1}}{2} \Leftrightarrow \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {x - 1} \right)\left( {x + 1 + a} \right)}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} =  - \dfrac{1}{2}$.

$ \Leftrightarrow \mathop {\lim }\limits_{x \to 1} \dfrac{{x + 1 + a}}{{x + 1}} =  - \dfrac{1}{2} \Leftrightarrow \dfrac{{2 + a}}{2} =  - \dfrac{1}{2} \Leftrightarrow a =  - 3$.

Suy ra $b = 2$.

Vậy ${a^2} + {b^2} = 13$.

Giả sử \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L,\mathop {\lim }\limits_{x \to {x_0}} g\left( x \right) = M\). Khi đó: \(\mathop {\lim }\limits_{x \to {x_0}} \left[ {f\left( x \right) + g\left( x \right)} \right] = L + M\)

\(\mathop {\lim }\limits_{x \to \sqrt 3 } \left| {{x^2} - 4} \right| = \left| {{{\left( {\sqrt 3 } \right)}^2} - 4} \right| = 1\)

Số \(L\) là: + giới hạn bên phải của hàm số \(y = f\left( x \right)\) kí hiệu là \(\mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = L\)

               + giới hạn bên trái của hàm số \(y = f\left( x \right)\) kí hiệu là \(\mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = L\)

Ta có: \(\mathop {\lim }\limits_{x \to  - \infty } \left( {\sqrt {{x^2} + ax + 5}  + x} \right) = 5\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to  - \infty } \left( {\dfrac{{{x^2} + ax + 5 - {x^2}}}{{\sqrt {{x^2} + ax + 5}  - x}}} \right) = 5\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to  - \infty } \left( {\dfrac{{ax + 5}}{{\sqrt {{x^2} + ax + 5}  - x}}} \right) = 5\)\( \Leftrightarrow \mathop {\lim }\limits_{x \to  - \infty } \left( {\dfrac{{a + \dfrac{5}{x}}}{{ - \sqrt {1 + \dfrac{a}{x} + \dfrac{5}{{{x^2}}}}  - 1}}} \right) = 5\)\( \Leftrightarrow \dfrac{a}{{ - 2}} = 5\)\( \Leftrightarrow a =  - 10\).

Vì vậy giá trị của \(a\) là một nghiệm của phương trình \({x^2} + 9x - 10 = 0\).

Cách 1 (Đặc biệt hóa)

Chọn \(f\left( x \right) = 10x\), ta có \(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 20}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{10x - 20}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{10\left( {x - 2} \right)}}{{x - 2}} = 10\)

Lúc đó \(T = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt[3]{{6f\left( x \right) + 5}} - 5}}{{{x^2} + x - 6}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt[3]{{60x + 5}} - 5}}{{{x^2} + x - 6}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt[3]{{60x + 5}} - 5}}{{\left( {x - 2} \right)\left( {x + 3} \right)}}\)

\( = \mathop {\lim }\limits_{x \to 2} \dfrac{{60x + 5 - {5^3}}}{{\left( {x - 2} \right)\left( {x + 3} \right)\left( {{{\sqrt[3]{{60x + 5}}}^2} + 5\sqrt[3]{{60x + 5}} + 25} \right)}}\)

\( = \mathop {\lim }\limits_{x \to 2} \dfrac{{60\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x + 3} \right)\left( {{{\sqrt[3]{{60x + 5}}}^2} + 5\sqrt[3]{{60x + 5}} + 25} \right)}}\)

\( = \mathop {\lim }\limits_{x \to 2} \dfrac{{60}}{{\left( {x + 3} \right)\left( {{{\sqrt[3]{{60x + 5}}}^2} + 5\sqrt[3]{{60x + 5}} + 25} \right)}} = \dfrac{4}{{25}}\)

Cách 2:

Chọn \(f\left( x \right) = 10x\), ta có \(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 20}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{10x - 20}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{10\left( {x - 2} \right)}}{{x - 2}} = 10\)

Sử dụng CASIO (chức năng CALC), nhập hàm cần tính giới hạn

Màn hình hiển thị

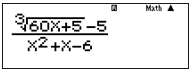
Thay giá trị \(x = 1,9999999\) vào

Màn hình hiển thị

Thay tiếp giá trị \(x = 2,0000001\) vào

Màn hình hiển thị

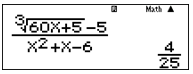
Cách 3:

Theo giả thiết có \(\mathop {\lim }\limits_{x \to 2} \left( {f\left( x \right) - 20} \right) = 0\) hay \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 20\) \(\left( * \right)\)

Khi đó $T = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt[3]{{6f\left( x \right) + 5}} - 5}}{{{x^2} + x - 6}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{6f\left( x \right) + 5 - 125}}{{\left( {{x^2} + x - 6} \right)\left[ {{{\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right)}^2} + 5\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right) + 25} \right]}}$

$T = \mathop {\lim }\limits_{x \to 2} \dfrac{{6\left[ {f\left( x \right) - 20} \right]}}{{\left( {x - 2} \right)\left( {x + 3} \right)\left[ {{{\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right)}^2} + 5\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right) + 25} \right]}}$

\(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 20}}{{x - 2}} = 10\)

\(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 20\\ \Rightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{6}{{\left( {x - 3} \right).\left[ {{{\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right)}^2} + 5\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right) + 25} \right]}}\\ = \dfrac{6}{{\left( {2 + 3} \right).\left[ {{{\left( {\sqrt[3]{{6.20 + 5}}} \right)}^2} + 5.\left( {\sqrt[3]{{6.20 + 5}}} \right) + 25} \right]}} = \dfrac{6}{{5.75}}\end{array}\)

$T = \dfrac{{10.6}}{{5.75}} = \dfrac{4}{{25}}$

\(\mathop {\lim }\limits_{x \to  - \infty } \left( {x - {x^3} + 1} \right) = \mathop {\lim }\limits_{x \to  - \infty } {x^3}\left( {\dfrac{1}{{{x^2}}} - 1 + \dfrac{1}{{{x^3}}}} \right) =  + \infty \) vì \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to  - \infty } {x^3} =  - \infty \\\mathop {\lim }\limits_{x \to  - \infty } \left( {\dfrac{1}{{{x^2}}} - 1 + \dfrac{1}{{{x^3}}}} \right) =  - 1 < 0\end{array} \right..\)

Ta có: \(I = \mathop {\lim }\limits_{x \to  + \infty } \left( {x + 1 - \sqrt {{x^2} - x + 2} } \right)\)$ \Leftrightarrow I = \mathop {\lim }\limits_{x \to  + \infty } \left( {\dfrac{{{x^2} - {x^2} + x - 2}}{{x + \sqrt {{x^2} - x + 2} }} + 1} \right)$$ \Leftrightarrow I = \mathop {\lim }\limits_{x \to  + \infty } \left( {\dfrac{{x - 2}}{{x + \sqrt {{x^2} - x + 2} }} + 1} \right)$$ \Leftrightarrow I = \mathop {\lim }\limits_{x \to  + \infty } \left( {\dfrac{{1 - \dfrac{2}{x}}}{{1 + \sqrt {1 - \dfrac{1}{x} + \dfrac{2}{{{x^2}}}} }} + 1} \right)$\( \Leftrightarrow I = \dfrac{3}{2}\).

Ta có: \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = L \Leftrightarrow \mathop {\lim }\limits_{x \to x_0^ + } f\left( x \right) = \mathop {\lim }\limits_{x \to x_0^ - } f\left( x \right) = L\)

Đặt \(L = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{x}{{\sqrt[7]{{x + 1}}.\sqrt {x + 4}  - 2}}} \right) = \dfrac{a}{b}\) thì \(\dfrac{1}{L} = \lim \left( {\dfrac{{\sqrt[7]{{x + 1}}.\sqrt {x + 4}  - 2}}{x}} \right) = \dfrac{b}{a}\).

Ta có

$\dfrac{b}{a} = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sqrt[7]{{x + 1}}.\sqrt {x + 4}  - \sqrt {x + 4}  + \sqrt {x + 4}  - 2}}{x}} \right) = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sqrt[7]{{x + 1}}.\sqrt {x + 4}  - \sqrt {x + 4} }}{x}} \right) + \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sqrt {x + 4}  - 2}}{x}} \right)$

Xét ${L_1} = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sqrt {x + 4} \left( {\sqrt[7]{{x + 1}} - 1} \right)}}{x}} \right)$. Đặt \(t = \sqrt[7]{{x + 1}}\). Khi đó :\(\left\{ \begin{array}{l}x = {t^7} - 1\\x \to 0 \Rightarrow t \to 1\end{array} \right.\)

\({L_1} = \mathop {\lim }\limits_{t \to 1} \dfrac{{\sqrt {{t^7} + 3} \left( {t - 1} \right)}}{{{t^7} - 1}} = \mathop {\lim }\limits_{t \to 1} \dfrac{{\sqrt {{t^7} + 3} }}{{\left( {{t^6} + {t^5} + {t^4} + {t^3} + {t^2} + t + 1} \right)}} = \dfrac{2}{7}\)

Xét ${L_2} = \mathop {\lim }\limits_{x \to 0} \left( {\dfrac{{\sqrt {x + 4}  - 2}}{x}} \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{\left( {\sqrt {x + 4}  - 2} \right)\left( {\sqrt {x + 4}  + 2} \right)}}{{x\left( {\sqrt {x + 4}  + 2} \right)}} = \mathop {\lim }\limits_{x \to 0} \dfrac{1}{{\sqrt {x + 4}  + 2}} = \dfrac{1}{4}$

Vậy \(\dfrac{b}{a} = \dfrac{2}{7} + \dfrac{1}{4} = \dfrac{{15}}{{28}}\)\( \Rightarrow a = 28,b = 15 \Rightarrow a + b = 43\) \( \Rightarrow a + b = 43\).

Vì \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} \left( {x - 15} \right) =  - 13 < 0\\\mathop {\lim }\limits_{x \to {2^ + }} \left( {x - 2} \right) = 0\\x - 2 > 0,\forall x > 2\end{array} \right.\) \( \Rightarrow \mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{x - 15}}{{x - 2}} =  - \infty \)

Ta có

\(\begin{array}{l}{u_2} = {u_1} + 4.1 + 3\\{u_3} = {u_2} + 4.2 + 3\\...\\{u_n} = {u_{n - 1}} + 4.\left( {n - 1} \right) + 3\end{array}\)

Cộng vế theo vế và rút gọn ta được

\({u_n} = {u_1} + 4.\left( {1 + 2 + ... + n - 1} \right) + 3\left( {n - 1} \right)\)\( = 4\dfrac{{n\left( {n - 1} \right)}}{2} + 3\left( {n - 1} \right)\)\( = 2{n^2} + n - 3\), với mọi $n \ge 1$.

Suy ra                                                           

\(\begin{array}{l}{u_{2n}} = 2{\left( {2n} \right)^2} + 2n - 3\\{u_{{2^2}n}} = 2{\left( {{2^2}n} \right)^2} + {2^2}n - 3\\...\\{u_{{2^{2018}}n}} = 2{\left( {{2^{2018}}n} \right)^2} + {2^{2018}}n - 3\end{array}\)

Và

\(\begin{array}{l}{u_{4n}} = 2{\left( {4n} \right)^2} + 4n - 3\\{u_{{4^2}n}} = 2{\left( {{4^2}n} \right)^2} + {4^2}n - 3\\...\\{u_{{4^{2018}}n}} = 2{\left( {{4^{2018}}n} \right)^2} + {4^{2018}}n - 3\end{array}\)

Do đó \(\lim \dfrac{{\sqrt {{u_n}}  + \sqrt {{u_{4n}}}  + \sqrt {{u_{{4^2}n}}}  + ... + \sqrt {{u_{{4^{2018}}n}}} }}{{\sqrt {{u_n}}  + \sqrt {{u_{2n}}}  + \sqrt {{u_{{2^2}n}}}  + ... + \sqrt {{u_{{2^{2018}}n}}} }}\)

$ = \lim \dfrac{{\sqrt {2 + \dfrac{1}{n} - \dfrac{3}{{{n^2}}}}  + \sqrt {{{2.4}^2} + \dfrac{4}{n} - \dfrac{3}{{{n^2}}}}  + ... + \sqrt {2{{\left( {{4^{2018}}} \right)}^2} + \dfrac{{{4^{2018}}}}{n} - \dfrac{3}{{{n^2}}}} }}{{\sqrt {2 + \dfrac{1}{n} - \dfrac{3}{{{n^2}}}}  + \sqrt {{{2.2}^2} + \dfrac{2}{n} - \dfrac{3}{{{n^2}}}}  + ... + \sqrt {2{{\left( {{2^{2018}}} \right)}^2} + \dfrac{{{2^{2018}}}}{n} - \dfrac{3}{{{n^2}}}} }}$

\( = \dfrac{{\sqrt 2 \left( {1 + 4 + {4^2} + ... + {4^{2018}}} \right)}}{{\sqrt 2 \left( {1 + 2 + {2^2} + ... + {2^{2018}}} \right)}}\)$ = \dfrac{{1\dfrac{{1 - {4^{2019}}}}{{1 - 4}}}}{{\dfrac{{1 - {2^{2019}}}}{{1 - 2}}}}$$ = \dfrac{1}{3}\dfrac{{{4^{2019}} - 1}}{{{2^{2019}} - 1}}$\( = \dfrac{{{2^{2019}} + 1}}{3}\).

Vì \({2^{2019}} > 2019\) cho nên sự xác định ở trên là duy nhất nên \(\left\{ \begin{array}{l}a = 2\\b = 1\\c = 3\end{array} \right.\)

Vậy \(S = a + b - c = 0\).

Ta có: \(\mathop {\lim }\limits_{x \to  \pm \infty } c = c,\mathop {\lim }\limits_{x \to  \pm \infty } \dfrac{c}{{{x^k}}} = 0\) nên đáp án A đúng.

Bước 1: Tính $\mathop {\lim }\limits_{x \to 1} f\left( x \right)$

Đặt \(\dfrac{{f\left( x \right) - 16}}{{x - 1}} = g\left( x \right) \Rightarrow f\left( x \right) = \left( {x - 1} \right)g\left( x \right) + 16\)

\( \Rightarrow \mathop {\lim }\limits_{x \to 1} f\left( x \right) = 16\).

Bước 2: Tính I

\(I = \mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 16}}{{\left( {x - 1} \right)\left( {\sqrt {2f\left( x \right) + 4}  + 6} \right)}}\)\( = \mathop {\lim }\limits_{x \to 1} \dfrac{{f\left( x \right) - 16}}{{x - 1}}.\dfrac{1}{{\sqrt {2f\left( x \right) + 4} {\rm{\;}} + 6}}\) \( = 24.\dfrac{1}{{\sqrt {2.16 + 4}  + 6}} = 2\)

Ta có: \(\mathop {\lim }\limits_{x \to  + \infty } f\left( x \right) =  + \infty  \Leftrightarrow \mathop {\lim }\limits_{x \to  + \infty } \left[ { - f\left( x \right)} \right] =  - \infty \)

\(\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} + 1}  + x} \right) = \mathop {\lim }\limits_{x \to  + \infty } x\left( {\sqrt {1 + \dfrac{1}{{{x^2}}}}  + 1} \right) =  + \infty \) vì \(\left\{ \begin{array}{l}\mathop {\lim }\limits_{x \to  + \infty } x =  + \infty \\\mathop {\lim }\limits_{x \to  + \infty} \sqrt {1 + \dfrac{1}{{{x^2}}}}  + 1 = 2 > 0\end{array} \right..\)