Cho \(f\left( x \right)\) là đa thức thỏa mãn \(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 20}}{{x - 2}} = 10\). Tính \(T = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt[3]{{6f\left( x \right) + 5}} - 5}}{{{x^2} + x - 6}}\)

Cách 1 (Đặc biệt hóa)

Chọn \(f\left( x \right) = 10x\), ta có \(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 20}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{10x - 20}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{10\left( {x - 2} \right)}}{{x - 2}} = 10\)

Lúc đó \(T = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt[3]{{6f\left( x \right) + 5}} - 5}}{{{x^2} + x - 6}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt[3]{{60x + 5}} - 5}}{{{x^2} + x - 6}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt[3]{{60x + 5}} - 5}}{{\left( {x - 2} \right)\left( {x + 3} \right)}}\)

\( = \mathop {\lim }\limits_{x \to 2} \dfrac{{60x + 5 - {5^3}}}{{\left( {x - 2} \right)\left( {x + 3} \right)\left( {{{\sqrt[3]{{60x + 5}}}^2} + 5\sqrt[3]{{60x + 5}} + 25} \right)}}\)

\( = \mathop {\lim }\limits_{x \to 2} \dfrac{{60\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x + 3} \right)\left( {{{\sqrt[3]{{60x + 5}}}^2} + 5\sqrt[3]{{60x + 5}} + 25} \right)}}\)

\( = \mathop {\lim }\limits_{x \to 2} \dfrac{{60}}{{\left( {x + 3} \right)\left( {{{\sqrt[3]{{60x + 5}}}^2} + 5\sqrt[3]{{60x + 5}} + 25} \right)}} = \dfrac{4}{{25}}\)

Cách 2:

Chọn \(f\left( x \right) = 10x\), ta có \(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 20}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{10x - 20}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{10\left( {x - 2} \right)}}{{x - 2}} = 10\)

Sử dụng CASIO (chức năng CALC), nhập hàm cần tính giới hạn

Màn hình hiển thị

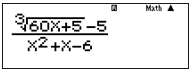
Thay giá trị \(x = 1,9999999\) vào

Màn hình hiển thị

Thay tiếp giá trị \(x = 2,0000001\) vào

Màn hình hiển thị

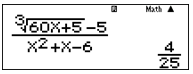
Cách 3:

Theo giả thiết có \(\mathop {\lim }\limits_{x \to 2} \left( {f\left( x \right) - 20} \right) = 0\) hay \(\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 20\) \(\left( * \right)\)

Khi đó $T = \mathop {\lim }\limits_{x \to 2} \dfrac{{\sqrt[3]{{6f\left( x \right) + 5}} - 5}}{{{x^2} + x - 6}} = \mathop {\lim }\limits_{x \to 2} \dfrac{{6f\left( x \right) + 5 - 125}}{{\left( {{x^2} + x - 6} \right)\left[ {{{\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right)}^2} + 5\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right) + 25} \right]}}$

$T = \mathop {\lim }\limits_{x \to 2} \dfrac{{6\left[ {f\left( x \right) - 20} \right]}}{{\left( {x - 2} \right)\left( {x + 3} \right)\left[ {{{\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right)}^2} + 5\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right) + 25} \right]}}$

\(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - 20}}{{x - 2}} = 10\)

\(\begin{array}{l}\mathop {\lim }\limits_{x \to 2} f\left( x \right) = 20\\ \Rightarrow \mathop {\lim }\limits_{x \to 2} \dfrac{6}{{\left( {x - 3} \right).\left[ {{{\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right)}^2} + 5\left( {\sqrt[3]{{6f\left( x \right) + 5}}} \right) + 25} \right]}}\\ = \dfrac{6}{{\left( {2 + 3} \right).\left[ {{{\left( {\sqrt[3]{{6.20 + 5}}} \right)}^2} + 5.\left( {\sqrt[3]{{6.20 + 5}}} \right) + 25} \right]}} = \dfrac{6}{{5.75}}\end{array}\)

$T = \dfrac{{10.6}}{{5.75}} = \dfrac{4}{{25}}$