Thể tích khối hộp

Công thức tính thể tích lăng trụ có diện tích đáy \(S\) và chiều cao \(h\) là \(V = Sh\).

Vì \(M \in \left( {A'B'C'} \right) \Rightarrow d\left( {M;\left( {ABC} \right)} \right) = d\left( {\left( {A'B'C'} \right);\left( {ABC} \right)} \right)\)

\( \Rightarrow {V_{M.ABC}} = \dfrac{1}{3}d\left( {M;\left( {ABC} \right)} \right).{S_{ABC}} = \dfrac{1}{3}V\)

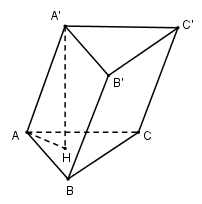
Gọi $H$ là hình chiếu vuông góc của $A'$  trên \(\left( {ABC} \right) \Rightarrow A'H \bot \left( {ABC} \right)\)

\( \Rightarrow AH\) là hình chiếu vuông góc của $AA'$  trên \(\left( {ABC} \right) \Rightarrow \widehat {\left( {AA';\left( {ABC} \right)} \right)} = \widehat {\left( {AA';AH} \right)} = \widehat {A'AH} = {60^0}\)

\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot AH \Rightarrow \Delta A'AH\) vuông tại \(H \Rightarrow A'H = AA'.\sin 60 = a\sqrt 3 .\dfrac{{\sqrt 3 }}{2} = \dfrac{{3a}}{2}\)

Tam giác $ABC$ đều cạnh  nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \dfrac{{3a}}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^3}\sqrt 3 }}{8}\)

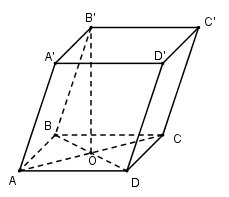
Gọi \(O = AC \cap BD\).

Xét tam giác $ABD$ có $AB = AD = a$ và \(\widehat {BAD} = {60^0} \Rightarrow \Delta ABD\) đều cạnh \(a \Rightarrow BD = a \Rightarrow BO = \dfrac{a}{2}\)

\( \Rightarrow B'O \bot \left( {ABCD} \right) \Rightarrow B'O \bot BO \Rightarrow \Delta BB'O\) vuông tại $O$

$ \Rightarrow B'O = \sqrt {BB{'^2} - B{O^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}$

\({S_{ABD}} = \dfrac{{{a^2}\sqrt 3 }}{4} \Rightarrow {S_{ABCD}} = 2{S_{ABD}} = \dfrac{{{a^2}\sqrt 3 }}{2}\)

Vậy \({V_{ABCD.A'B'C'D'}} = B'O.{S_{ABCD}} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}}}{4}\)

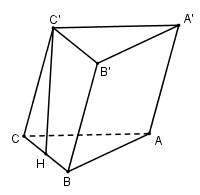
Áp dụng định lí Côsin trong tam giác $ABC$ có: \(BC = \sqrt {A{B^2} + A{C^2} - 2AB.AC.\cos 120}  \)

$= \sqrt {4{a^2} + {a^2} - 2.2a.a.\dfrac{{ - 1}}{2}}  = a\sqrt 7  \Rightarrow CH = \dfrac{1}{2}BC = \dfrac{{a\sqrt 7 }}{2}$

\(C'H \bot \left( {ABC} \right) \Rightarrow C'H \bot CH \Rightarrow \Delta CC'H\) vuông tại $H$

\( \Rightarrow C'H = \sqrt {CC{'^2} - C{H^2}}  = \sqrt {\dfrac{{10{a^2}}}{4} - \dfrac{{7{a^2}}}{4}}  = \dfrac{{a\sqrt 3 }}{2}\)

\({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin 120 = \dfrac{1}{2}.2a.a.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{2}\)

Vậy \({V_{ABC.A'B'C'}} = C'H.{S_{ABC}} = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}}}{4}\)

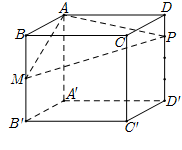
Áp dụng công thức tính nhanh, ta có:

$\dfrac{{{V_{AMNPBCD}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{2}\left( {\dfrac{{BM}}{{BB'}} + \dfrac{{DP}}{{DD'}}} \right) = \dfrac{3}{8} \Rightarrow \,\,{V_{AMNPBCD}} = 3{a^3}.$

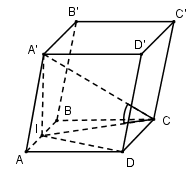
Theo bài ra ta có: $IC$ là hình chiếu vuông góc của $A'C$  trên $\left( {ABCD} \right)$

\( \Rightarrow \widehat {\left( {A'C;\left( {ABCD} \right)} \right)} = \widehat {\left( {A'C;IC} \right)} = \widehat {A'CI} = \alpha \)

Xét tam giác vuông $IBC$ có: \(IC = \sqrt {I{B^2} + B{C^2}}  = \sqrt {\dfrac{{{a^2}}}{4} + {a^2}}  = \dfrac{{a\sqrt 5 }}{2}\)

Xét tam giác vuông $A'IC$  có: \(A'I = IC.\tan \alpha  = \dfrac{{a\sqrt 5 }}{2}.\dfrac{2}{{\sqrt 5 }} = a\)

\({S_{\Delta ICD}} = \dfrac{1}{2}d\left( {I;CD} \right).CD = \dfrac{1}{2}a.a = \dfrac{{{a^2}}}{2}\)

Vậy \({V_{A'.ICD}} = \dfrac{1}{3}A'I.{S_{\Delta ICD}} = \dfrac{1}{3}.a.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{6}\)

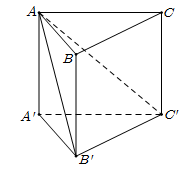
Dựng $B'M \bot A'C' \Rightarrow B'M \bot \left( {ACC'A'} \right)$

Dựng $MN \bot AC' \Rightarrow AC' \bot \left( {MNB'} \right)$

Khi đó $\widehat {\left( {\left( {AB'C'} \right);\left( {AC'A'} \right)} \right)} = \widehat {MNB'} = {60^0}$

Ta có: $B'M = \dfrac{{a\sqrt 2 }}{2} \Rightarrow MN = \dfrac{{B'M}}{{\tan \widehat {MNB'}}} = \dfrac{{a\sqrt 6 }}{6}$

Mặt khác $\tan \widehat {AC'A'} = \dfrac{{MN}}{{C'N}} = \dfrac{{AA'}}{{A'C'}}$

Trong đó $MN = \dfrac{{a\sqrt 6 }}{6};MC' = \dfrac{{a\sqrt 2 }}{2} \Rightarrow C'N = \sqrt {C'{M^2} - M{N^2}}  = \dfrac{{a\sqrt 3 }}{3}$

Suy ra $AA' = a$

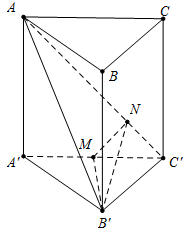
Thể tích lăng trụ $V = \dfrac{{A{B^2}}}{2}.AA' = \dfrac{{{a^3}}}{2}$$ \Rightarrow {V_{B'.ACC'A'}} = V - {V_{B'.BAC}} = V - \dfrac{V}{3} = \dfrac{2}{3}V = \dfrac{{{a^3}}}{3}.$

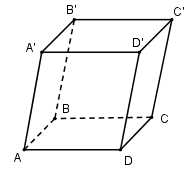
Dựng khối hộp $ABCD.A’B’C’D’$ ta có: \({V_{ABC.A'B'C'}} = \dfrac{1}{2}{V_{ABCD.A'B'C'D'}}\)

Khối hộp \(ABCD.A'B'C'D'\) có hai đáy là $ABB’A’$ và $CDD’C’$

\( \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABB'A'}}.h\)

Trong đó \(h = d\left( {\left( {ABB'A'} \right);\left( {CDD'C'} \right)} \right) = d\left( {CC';\left( {ABB'A'} \right)} \right) = 7\)

\( \Rightarrow {V_{ABCD.A'B'C'D'}} = 4.7 = 28\)

Vậy \({V_{ABC.A'B'C'}} = \dfrac{1}{2}.28 = 14\)

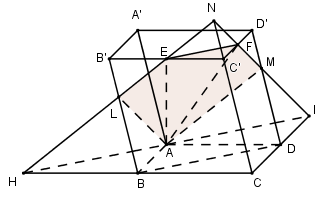
Mặt phẳng \(\left( {AEF} \right)\) chứa \(EF//BD \subset \left( {ABCD} \right)\)

\( \Rightarrow \) Giao tuyến của \(\left( {AEF} \right)\) và \(\left( {ABCD} \right)\) là đường thẳng đi qua \(A\) và song song với \(EF\)

Trong \(\left( {ABCD} \right)\) qua \(A\) kẻ \(HI//BD\,\,\left( {H \in BC,I \in CD} \right)\)

Trong \(\left( {BCC'B'} \right)\) gọi \(L = EH \cap BB'\), trong \(\left( {CDD'C'} \right)\) gọi \(M = FI \cap DD'\), khi đó \(\left( {AEF} \right) \equiv \left( {ALEFM} \right)\)

Ta có : \(\left\{ \begin{array}{l}\left( {AEF} \right) \cap \left( {BCC'B'} \right) = HE\\\left( {AEF} \right) \cap \left( {CDD'C'} \right) = FI\\\left( {BCC'B'} \right) \cap \left( {CDD'C'} \right) = CC'\end{array} \right. \)

\(\Rightarrow HE,FI,CC'\) đồng quy tại \(N\).

Ta có : \({V_{H'}} = {V_{N.CIH}} - {V_{N.EFC'}} - {V_{L.ABH}} - {V_{M.ADI}}\)

Ta dễ dàng chứng minh được \(B,D\) lần lượt là trung điểm của \(CH,CI \Rightarrow BD = \dfrac{1}{2}HI \Rightarrow EF = \dfrac{1}{2}BD = \dfrac{1}{4}HI\)

\( \Rightarrow \Delta C'EF\) đồng dạng với \(\Delta CIH\) theo tỉ số đồng dạng \(k = \dfrac{1}{4} \Rightarrow \dfrac{{{S_{\Delta C'EF}}}}{{{S_{\Delta CIH}}}} = \dfrac{1}{{16}}\)

 $\begin{array}{l}\dfrac{{NC'}}{{NC}} = \dfrac{{EC'}}{{HC}} = \dfrac{1}{4} \Rightarrow \dfrac{{d\left( {N';\left( {C'EF} \right)} \right)}}{{d\left( {N;\left( {CIH} \right)} \right)}} = \dfrac{1}{4}\\ \Rightarrow {V_{N.EFC'}} = \dfrac{1}{{16}}.\dfrac{1}{4}{V_{N.CIH}} = \dfrac{1}{{64}}{V_{N.CIH}}\\{V_{LABH}} = {V_{M.ADI}} = \dfrac{1}{2}.\dfrac{1}{4}{V_{N.CIH}} = \dfrac{1}{8}{V_{N.CIH}}\\ \Rightarrow {V_{H'}} = {V_{N.CIH}} - {V_{N.EFC'}} - {V_{L.ABH}} - {V_{M.ADI}} = \dfrac{{47}}{{64}}{V_{N.CIH}}\end{array}$

 Ta có :

\(\begin{array}{l}\dfrac{{CC'}}{{NC}} = \dfrac{3}{4},\dfrac{{{S_{ABCD}}}}{{{S_{CIH}}}} = \dfrac{1}{2} \Rightarrow \dfrac{{{V_{ABCD.A'B'C'D'}}}}{{{V_{S.CIH}}}} = \dfrac{{d\left( {C';\left( {ABCD} \right)} \right).{S_{ABCD}}}}{{\dfrac{1}{3}d\left( {N;\left( {CIH} \right)} \right).{S_{CIH}}}} = 3.\dfrac{{CC'}}{{NC}}.\dfrac{{{S_{ABCD}}}}{{{S_{CIH}}}} = 3.\dfrac{3}{4}.\dfrac{1}{2} = \dfrac{9}{8}\\ \Rightarrow {V_{S.CIH}} = \dfrac{8}{9}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow {V_{H'}} = \dfrac{{47}}{{64}}{V_{N.CIH}} = \dfrac{{47}}{{72}}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow {V_H} = \dfrac{{25}}{{72}}{V_{ABCD.A'B'C'D'}}\\ \Rightarrow \dfrac{{{V_H}}}{{{V_{H'}}}} = \dfrac{{25}}{{47}}\end{array}\)

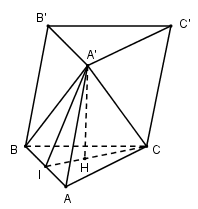
Gọi $H$ là tâm tam giác đều $ABC$ . Vì $A'A = A'B = A'C$ nên hình chóp $A'.ABC$  là đều nên \(A'H \bot \left( {ABC} \right)\)

Gọi $I$ là trung điểm của $AB$.

Vì tam giác $ABC$ đều cạnh $a$ nên \(CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow HI = \dfrac{1}{3}CI = \dfrac{{a\sqrt 3 }}{6}\)

Tam giác $A'AB$  cân tại $A'$  nên \(A'I \bot AB \Rightarrow \Delta A'AI\) vuông tại \(I \Rightarrow A'I = \sqrt {AA{'^2} - A{I^2}}  = \sqrt {\dfrac{{7{a^2}}}{{12}} - \dfrac{{{a^2}}}{4}}  = \dfrac{a}{{\sqrt 3 }}\)

\(A'H \bot \left( {ABC} \right) \Rightarrow A'H \bot HI \Rightarrow \Delta A'HI\) vuông tại \(H \Rightarrow A'H = \sqrt {A'{I^2} - H{I^2}}  = \sqrt {\dfrac{{{a^2}}}{3} - \dfrac{{{a^2}}}{{12}}}  = \dfrac{a}{2}\)

Vì tam giác $ABC$ đều cạnh $a$ nên \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)

Vậy \({V_{ABC.A'B'C'}} = A'H.{S_{ABC}} = \dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\)

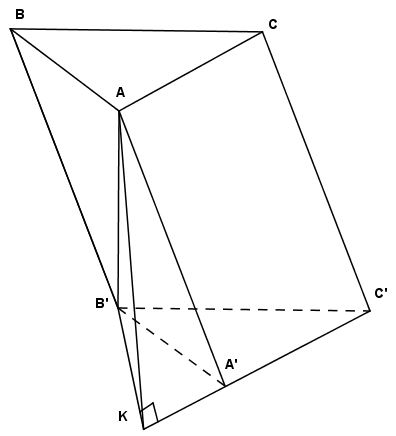
Trong (A’B’C’) kẻ \(B'K \bot A'C'\,\,\left( {K \in A'C'} \right)\)

Ta có:

\(\left. \begin{array}{l}AB' \bot A'C'\left( {AB' \bot \left( {A'B'C'} \right)} \right)\\B'K \bot A'C'\end{array} \right\} \Rightarrow A'C' \bot \left( {AB'K} \right) \Rightarrow A'C' \bot AK\)

\(\left. \begin{array}{l}\left( {AA'C'} \right) \cap \left( {A'B'C'} \right) = A'C'\\\left( {AA'C'} \right) \supset AK \bot A'C'\\\left( {A'B'C'} \right) \supset B'K \bot A'C'\end{array} \right\} \Rightarrow \widehat {\left( {\left( {AA'C'} \right);\left( {A'B'C'} \right)} \right)} = \widehat {\left( {AK;B'K} \right)} = \widehat {AKB'} = {30^0}\)

Ta có:

\(\begin{array}{l}{S_{A'B'C'}} = \dfrac{1}{2}A'B'.A'C'.\sin 120 = \dfrac{1}{2}{a^2}.\dfrac{{\sqrt 3 }}{2} = \dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{1}{2}B'K.A'C'\\ \Rightarrow B'K = \dfrac{{2{S_{A'B'C'}}}}{{A'C'}} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{2}}}{a} = \dfrac{{a\sqrt 3 }}{2}\end{array}\)

\(AB' \bot \left( {A'B'C'} \right) \Rightarrow AB' \bot B'K \Rightarrow \Delta AB'K\) vuông tại B’

$ \Rightarrow AB' = B'K.tan30 = \dfrac{{a\sqrt 3 }}{2}.\dfrac{{\sqrt 3 }}{3} = \dfrac{a}{2}$

Vậy \({V_{ABC.A'B'C'}} = AB'.{S_{A'B'C'}} = \dfrac{a}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{8}\)

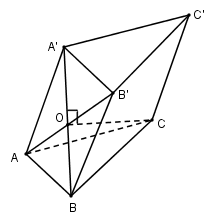
Gọi $O$ là tâm hình bình hành $ABB’A’$. Ta có \(CO \bot \left( {ABB'A'} \right) \Rightarrow CO \bot OA;CO \bot OB\)

\(\Delta COA = \Delta COB\left( {c.g.c} \right) \Rightarrow OA = OB \Rightarrow AB' = A'B \Rightarrow ABB'A'\) là hình chữ nhật.

Lại có \(AB = BB' = a \Rightarrow ABB'A'\) là hình vuông

Khi đó \(OA = OB = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }}\)

Xét tam giác vuông $OAC$ có: \(OC = \sqrt {A{C^2} - O{A^2}}  = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}}  = \dfrac{{a\sqrt 2 }}{2}\)

\( \Rightarrow {V_{C.A'AB}} = \dfrac{1}{3}OC.{S_{A'AB}} = \dfrac{1}{3}.\dfrac{{a\sqrt 2 }}{2}.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{{12}}\)

Mà ${V_{ABC.A'B'C'}} = {S_{ABC}}.d\left( {A',\left( {ABC} \right)} \right) = 3.\dfrac{1}{3}{S_{ABC}}.d\left( {A',\left( {ABC} \right)} \right) = 3.{V_{A'.ABC}}$

Vậy \({V_{ABC.A'B'C'}} = 3{V_{C.A'AB}} = \dfrac{{{a^3}\sqrt 2 }}{4}\)

Diện tích toàn phần của hình hộp chữ nhật: ${S_{tp}} = {S_{xq}} + 2ab = 2h\left( {a + b} \right) + 2ab.$

Thể tích hình hộp chữ nhật: $V = abh.$

Thể tích của lăng trụ là: $V = {S_d}.h.$

Diện tích toàn phần của khối lập phương: ${S_{tp}} = 6{a^2}.$

Thể tích của khối lập phương: $V = {a^3}.$

Thể tích khối chóp là: $V = \dfrac{1}{3}{S_d}.h.$

Do đó các đáp án B, C, D đúng, chỉ có A sai.

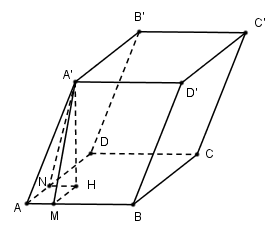
Kẻ \(A'H \bot \left( {ABCD} \right);HM \bot AB;HN \bot AD\)

Ta có: \(\left. \begin{array}{l}A'H \bot AB\\HM \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {A'HM} \right) \Rightarrow AB \bot A'M\)

\(\left. \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {ABCD} \right) = AB\\\left( {ABB'A'} \right) \supset A'M \bot AB\\\left( {ABCD} \right) \supset HM \bot AB\end{array} \right\} \Rightarrow \widehat {\left( {\left( {ABB'A'} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {A'M;HM} \right)} = \widehat {A'MH} = {45^o}\)

Chứng minh tương tự ta có \(\widehat {A'NH} = {60^0}\)

Đặt \(A'H = x\) khi đó ta có:

\(A'N = \dfrac{x}{{\sin 60}} = \dfrac{{2x}}{{\sqrt 3 }},AN = \sqrt {AA{'^2} - A'{N^2}}  = \sqrt {1 - \dfrac{{4{x^2}}}{3}}  = HM\)

Mà \(HM = x.\cot 45 = x\)

$ \Rightarrow x = \sqrt {1 - \dfrac{{4{x^2}}}{3}}  \Leftrightarrow {x^2} = 1 - \dfrac{{4{x^2}}}{3} \Leftrightarrow \dfrac{{7{x^2}}}{3} = 1 \Rightarrow {x^2} = \dfrac{3}{7} \Rightarrow x = \sqrt {\dfrac{3}{7}} $

\({S_{ABCD}} = \sqrt 3 .\sqrt 7  = \sqrt {21} \)

Vậy \({V_{ABCD.A'B'C'D'}} = A'H.{S_{ABCD}} = \sqrt {\dfrac{3}{7}} .\sqrt {21}  = 3\)

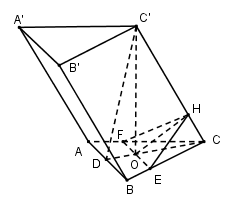
Gọi $D$ là trung điểm của $AB$. Trong $(CC’D)$ kẻ \(OH \bot CC' \Rightarrow OH = a\)

\(\left. \begin{array}{l}CD \bot AB\\C'O \bot AB\end{array} \right\} \Rightarrow AB \bot \left( {CC'D} \right) \Rightarrow AB \bot CC'\)

Trong $(ABC)$, qua $O$ kẻ $EF // AB$ \(\left( {E \in BC;F \in AC} \right)\)

Ta có: \(\left. \begin{array}{l}EF \bot CC'\\OH \bot CC'\end{array} \right\} \Rightarrow CC' \bot \left( {EFH} \right) \Rightarrow CC' \bot HE;CC' \bot HF\)

Ta có: \(\left. \begin{array}{l}\left( {ACC'A'} \right) \cap \left( {BCC'B'} \right) = CC'\\\left( {ACC'A'} \right) \supset HF \bot CC'\\\left( {BCC'B'} \right) \supset HE \bot CC'\end{array} \right\} \Rightarrow \widehat {\left( {\left( {ACC'A'} \right);\left( {BCC'B'} \right)} \right)} = \widehat {\left( {HF;HE} \right)} = {90^0} \Rightarrow HE \bot HF\)

\( \Rightarrow \Delta HEF\) vuông tại $H$

\(\Delta HCE = \Delta HCF\left( {c.g.v - c.h} \right) \Rightarrow HE = HF \Rightarrow \Delta HEF\) vuông cân tại H\( \Rightarrow EF = 2HO = 2a\)

Ta có: \(\dfrac{{EF}}{{AB}} = \dfrac{{CO}}{{CD}} = \dfrac{2}{3} \Rightarrow AB = \dfrac{3}{2}EF = \dfrac{3}{2}.2a = 3a\)\( \Rightarrow {S_{\Delta ABC}} = \dfrac{{A{B^2}\sqrt 3 }}{4} = \dfrac{{9{a^2}\sqrt 3 }}{4}\)

\(CD = \dfrac{{AB\sqrt 3 }}{2} = \dfrac{{3a\sqrt 3 }}{2} \Rightarrow CO = \dfrac{2}{3}AB = \dfrac{2}{3}.\dfrac{{3a\sqrt 3 }}{2} = a\sqrt 3 \)

\(C'O \bot \left( {ABC} \right) \Rightarrow C'O \bot CO \Rightarrow \Delta CC'O\) vuông tại O

\( \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{1}{{C'{O^2}}} + \dfrac{1}{{C{O^2}}} \Rightarrow \dfrac{1}{{C'{O^2}}} = \dfrac{1}{{O{H^2}}} - \dfrac{1}{{C{O^2}}} = \dfrac{1}{{{a^2}}} - \dfrac{1}{{3{a^2}}} = \dfrac{2}{{3{a^2}}} \Rightarrow C'O = \dfrac{{\sqrt 6 }}{2}a\)

Vậy ${V_{ABC.A'B'C'}} = C'O.{S_{\Delta ABC}} = \dfrac{{a\sqrt 6 }}{2}.\dfrac{{9{a^2}\sqrt 3 }}{4} = \dfrac{{27{a^3}\sqrt 2 }}{8}$

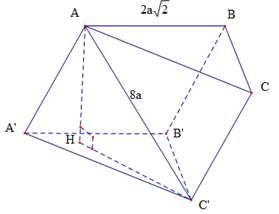
Gọi \(H\) là hình chiếu của \(A\) lên \(mp\left( {A'B'C'} \right)\).

\( \Rightarrow \widehat {HC'A} = {45^0}\).

\( \Rightarrow \Delta AHC'\) vuông cân tại $H.$

\( \Rightarrow AH = AC'.\sin 45^0=AC'.\dfrac{{\sqrt 2}}{{2}} =  4a\sqrt 2 .\)

Diện tích tam giác $ABC$ là: $S_{ABC}=\dfrac{(2a\sqrt{2})^2\sqrt{3}}{4}$

NX: \({V_{A.BCC'B'}} = \dfrac{2}{3}{V_{ABC.A'B'C'}} = \dfrac{2}{3}AH.{S_{ABC}} = \dfrac{2}{3}.4a\sqrt 2 .\dfrac{{{{\left( {2a\sqrt 2 } \right)}^2}.\sqrt 3 }}{4} = \dfrac{{16{a^3}\sqrt 6 }}{3}.\)

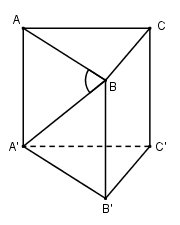
Vì \(AA' \bot \left( {ABC} \right) \Rightarrow AB\) là hình chiếu vuông góc của $A'B$ lên \( (ABC)\Rightarrow \widehat {\left( {A'B;\left( {ABC} \right)} \right)} = \widehat {\left( {A'B;AB} \right)} = \widehat {A'BA} = {30^0}\)

 Xét tam giác vuông $ABC$ có: \(AB = BC.\tan 60 = a\sqrt 3 \)

\(AA' \bot \left( {ABC} \right) \supset AB \Rightarrow AA' \bot AB \Rightarrow \Delta ABA'\) vuông tại $A$ \( \Rightarrow AA' = AB.\tan \widehat {A'BA} = a\sqrt 3 .\tan 30 = a\sqrt 3 .\dfrac{1}{{\sqrt 3 }} = a\)

\({S_{\Delta ABC}} = \dfrac{1}{2}AB.BC = \dfrac{1}{2}a\sqrt 3 .a = \dfrac{{{a^2}\sqrt 3 }}{2}\)

Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = a.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{2}\)

Gọi D là trung điểm của BC ta có:

Tam giác ABC đều nên \(AD \bot BC\) và $AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot BC$

\( \Rightarrow BC \bot \left( {AA'D} \right) \Rightarrow BC \bot A'D \Rightarrow \Delta A'BC\)cân tại A’

 Tam giác ABC đều cạnh \(a = 4 \Rightarrow AD = \dfrac{{4\sqrt 3 }}{2} = 2\sqrt 3 \)

\({S_{\Delta A'BC}} = \dfrac{1}{2}A'D.BC \Rightarrow A'D = \dfrac{{2{S_{\Delta A'BC}}}}{{BC}} = \dfrac{{2.8}}{4} = 4\)

Xét tam giác vuông  AA’D có: \(AA' = \sqrt {A'{D^2} - A{D^2}}  = \sqrt {16 - 12}  = 2\)

\({S_{ABC}} = \dfrac{{{4^2}\sqrt 3 }}{4} = 4\sqrt 3 \)

Vậy \({V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = 2.4\sqrt 3  = 8\sqrt 3 \)

Vì $A'B'C'D'$  là hình vuông cạnh $a$ nên \(B'D' = a\sqrt 2 \)

\(BB' \bot \left( {A'B'C'D'} \right) \Rightarrow BB' \bot B'D' \Rightarrow \Delta BB'D'\) vuông tại \(B' \Rightarrow BB' = \sqrt {BD{'^2} - B'D{'^2}}  = \sqrt {6{a^2} - 2{a^2}}  = 2a\)

Vậy \({V_{ABCD.A'B'C'D'}} = BB'.{S_{ABCD}} = 2a.{a^2} = 2{a^3}\)