Câu hỏi:
2 năm trước
Cho hình lăng trụ ABC.A′B′C′ có AB=2a,AC=a,AA′=a√102,^BAC=1200. Hình chiếu vuông góc của C′ lên (ABC) là trung điểm của cạnh BC. Tính thể tích khối lăng trụ ABC.A′B′C′ theo a?
Trả lời bởi giáo viên
Đáp án đúng: b
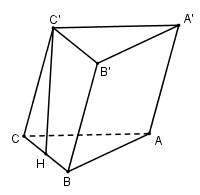
Áp dụng định lí Côsin trong tam giác ABC có: BC=√AB2+AC2−2AB.AC.cos120
=√4a2+a2−2.2a.a.−12=a√7⇒CH=12BC=a√72
C′H⊥(ABC)⇒C′H⊥CH⇒ΔCC′H vuông tại H
⇒C′H=√CC′2−CH2=√10a24−7a24=a√32
SABC=12AB.AC.sin120=12.2a.a.√32=a2√32
Vậy VABC.A′B′C′=C′H.SABC=a√32.a2√32=3a34
Hướng dẫn giải:
- Tính diện tích đáy SABC.
- Tính độ dài đường cao.
- Tính thể tích khối lăng trụ theo công thức V=Sh với S là diện tích đáy, h là chiều cao.