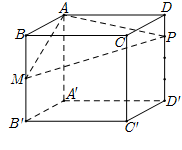
Cho hình lăng trụ ABCD.A′B′C′D′ có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của điểm A′ trên mặt phẳng (ABCD) là trung điểm I của cạnh AB. Biết A′C tạo với mặt phẳng đáy một góc α với tanα=2√5. Thể tích khối chóp A′.ICD là:
Trả lời bởi giáo viên
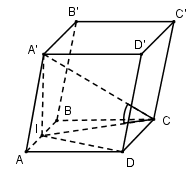
Theo bài ra ta có: IC là hình chiếu vuông góc của A′C trên (ABCD)
⇒^(A′C;(ABCD))=^(A′C;IC)=^A′CI=α
Xét tam giác vuông IBC có: IC=√IB2+BC2=√a24+a2=a√52
Xét tam giác vuông A′IC có: A′I=IC.tanα=a√52.2√5=a
SΔICD=12d(I;CD).CD=12a.a=a22
Vậy VA′.ICD=13A′I.SΔICD=13.a.a22=a36
Hướng dẫn giải:
- Xác định góc giữa đường thẳng và mặt phẳng: là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng.
- Tính độ dài đường cao A′I và diện tích đáy ICD.
- Tính thể tích khối lăng trụ theo công thức V=Sh với S là diện tích đáy, h là chiều cao.