Câu hỏi:
2 năm trước
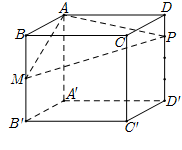
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(2a,\) gọi \(M\) là trung điểm của $BB'$ và \(P\) thuộc cạnh $DD'$ sao cho $DP\, = \,\dfrac{1}{4}DD'.$ Mặt phẳng $(AMP)$ cắt $CC'$ tại$N.$ Thể tích khối đa diện $AMNPBCD$ bằng
Trả lời bởi giáo viên
Đáp án đúng: b
Áp dụng công thức tính nhanh, ta có:
$\dfrac{{{V_{AMNPBCD}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{2}\left( {\dfrac{{BM}}{{BB'}} + \dfrac{{DP}}{{DD'}}} \right) = \dfrac{3}{8} \Rightarrow \,\,{V_{AMNPBCD}} = 3{a^3}.$
Hướng dẫn giải:
Dựa vào công thức tính nhanh tỉ số thể tích trong khối lăng trụ với đáy là tứ giác như sau:
Cho hình lăng trụ $ABCD.A'B'C'D'$. Mặt phẳng $(\alpha )$ cắt lăng trụ theo thiết diện là tứ giác $MNPQ$ với $M \in AA',\,\,N \in BB',\,\,P \in CC',\,\,Q \in DD'.$ Khi đó:
$\dfrac{{AM}}{{AA'}} + \dfrac{{CN}}{{CC'}} = \dfrac{{BP}}{{BB'}} + \dfrac{{DQ}}{{DD'}}$ và $\dfrac{{{V_{ABCD.MNPQ}}}}{{{V_{ABCD.A'B'C'D'}}}} = \dfrac{1}{2}\left( {\dfrac{{AM}}{{AA'}} + \dfrac{{CN}}{{CC'}}} \right) = \dfrac{1}{2}\left( {\dfrac{{BP}}{{BB'}} + \dfrac{{DQ}}{{DD'}}} \right)$
