Lăng trụ đứng tứ giác có đáy là hình thoi mà các đường chéo là \(6cm\) và \(8cm\), biết rằng chu vi đáy bằng 2 lần chiều cao lăng trụ. Tính thể tích khối lăng trụ
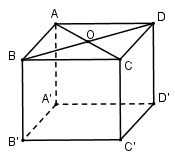
Gọi \(O = AC \cap BD\) ta có: \(OA = 3cm\,;\,OB = 4cm\)
Xét tam giác vuông $OAB$ có: \(AB = \sqrt {O{A^2} + O{B^2}} = \sqrt {{3^2} + {4^2}} = 5cm\).
Khi đó chu vi đáy bằng \(P = 4.5 = 20 = 2AA' \Rightarrow AA' = 10\left( {cm} \right)\)
\({S_{ABCD}} = \dfrac{1}{2}AC.BD = \dfrac{1}{2}.6.8 = 24\left( {c{m^2}} \right)\)
Vậy \({V_{ABCD.A'B'C'D'}} = AA'.{S_{ABCD}} = 10.24 = 240\left( {c{m^3}} \right)\)
Cho lăng trụ đứng \(ABC.A'B'C'\) với $ABC$ là tam giác vuông cân tại $C$ có \(AB = a\) , mặt bên \(ABB'A'\) là hình vuông. Mặt phẳng qua trung điểm $I$ của $AB$ và vuông góc với \(AB'\) chia khối lăng trụ thành 2 phần. Tính thể tích mỗi phần?
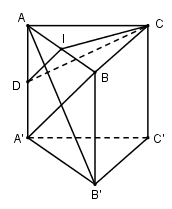
Gọi $D$ là trung điểm của $AA'$ ta có $ID$ là đường trung bình của tam giác \(AA'B \Rightarrow ID//A'B\)
Mà \(A'B \bot AB'\) (do \(ABB'A'\) là hình vuông)
\( \Rightarrow ID \bot AB'\)
Tam giác $ABC$ vuông cân tại $C$ nên \(IC \bot AB\). Mà \(AA' \bot \left( {ABC} \right) \Rightarrow AA' \bot IC\)
\( \Rightarrow IC \bot \left( {ABB'A'} \right) \Rightarrow IC \bot AB'\)
\( \Rightarrow AB' \bot \left( {ICD} \right)\)
\( \Rightarrow \) Mặt phẳng qua $I$ và vuông góc với $AB'$ là \(\left( {ICD} \right)\)
Tam giác $ABC$ vuông cân tại $C$ nên \(AC = BC = \dfrac{{AB}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }} \Rightarrow {S_{ABC}} = \dfrac{1}{2}AC.BC = \dfrac{1}{2}\dfrac{a}{{\sqrt 2 }}\dfrac{a}{{\sqrt 2 }} = \dfrac{{{a^2}}}{4}\)
\(ABB'A'\) là hình vuông \( \Rightarrow AA' = AB = a\)
\( \Rightarrow {V_{ABC.A'B'C'}} = AA'.{S_{ABC}} = a.\dfrac{{{a^2}}}{4} = \dfrac{{{a^3}}}{4} = V\)
Ta có: \({V_{D.ACI}} = \dfrac{1}{3}AD.{S_{ACI}} = \dfrac{1}{3}.\dfrac{1}{2}AA'.\dfrac{1}{2}{S_{ABC}} = \dfrac{1}{{12}}{V_{ABC.A'B'C'}} = \dfrac{1}{{12}}.\dfrac{{{a^3}}}{4} = \dfrac{{{a^3}}}{{48}} = {V_1}\)
\( \Rightarrow {V_2} = V - {V_1} = \dfrac{{{a^3}}}{4} - \dfrac{{{a^3}}}{{48}} = \dfrac{{11{a^3}}}{{48}}\)
Cho đa diện \(ABCDEF\) có \(AD,BE,CF\) đôi một song song. \(AD \bot \left( {ABC} \right)\), \(AD + BE + CF = 5\), diện tích tam giác \(ABC\) bằng \(10\). Thể tích đa diện \(ABCDEF\) bằng
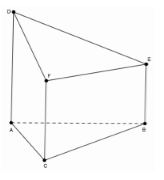
Chọn \(AD = BE = CF = \dfrac{5}{3}\) thì đa diện là hình lăng trụ đứng \(ABC.DEF\) có diện tích đáy \({S_{ABC}} = 10\) và chiều cao \(AD = \dfrac{5}{3}\).
Thể tích \(V = {S_{ABC}}.AD = 10.\dfrac{5}{3} = \dfrac{{50}}{3}\).
Cho hình hộp \(ABCD.A'B'C'D'\) có thể tích bằng \(V\). Gọi \(M,\,\,N,\,\,P,\,\,Q,\,\,E,\,\,F\) lần lượt là tâm các hình bình hành \(ABCD,\,\,A'B'C'D',\,\,ABB'A',\,\,BCC'B',\,\,CDD'C',\,\,DAA'D'\). Thể tích khối đa diện có các đỉnh \(M,\,\,P,\,\,Q,\,\,E,\,\,F,\,\,N\) bằng:
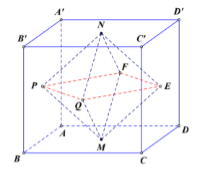
Đặc biệt hóa, coi \(ABCD.A'B'C'D'\) là khối lập phương cạnh bằng 1 \( \Rightarrow {V_{ABCD.A'B'C'D'}} = 1 = V\).
Dễ thấy \(MNPQEF\) là khối bát diện đều cạnh cạnh \(QE = \dfrac{1}{2}BD = \dfrac{{\sqrt 2 }}{2}\).
Vậy \({V_{MNPQEF}} = \dfrac{{{{\left( {\dfrac{{\sqrt 2 }}{2}} \right)}^3}\sqrt 2 }}{3} = \dfrac{1}{6} = \dfrac{V}{6}\).
Cho hình lăng trụ \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A.\) Cạnh \(BC = 2a\) và \(\angle ABC = {60^0}.\) Biết tứ giác \(BCC'B'\) là hình thoi có \(\angle B'BC\) nhọn. Mặt phẳng \(\left( {BCC'B'} \right)\) vuông góc với \(\left( {ABC} \right)\) và mặt phẳng \(\left( {ABB'A'} \right)\) tạo với \(\left( {ABC} \right)\) góc \({45^0}.\) Thể tích khối lăng trụ \(ABC.A'B'C'\) bằng:
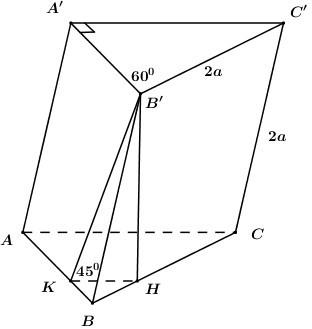
Trong \(\left( {BCC'B'} \right)\) kẻ \(B'H \bot BC\,\,\left( {H \in BC} \right)\) (do \(\angle B'BC\) nhọn).
Trong \(\left( {ABC} \right)\) kẻ \(HK\parallel AC \Rightarrow HK \bot AB\) ta có: \(\left\{ \begin{array}{l}AB \bot HK\\AB \bot B'H\end{array} \right. \Rightarrow AB \bot \left( {B'HK} \right) \Rightarrow AB \bot B'K\).
Ta có: \(\left\{ \begin{array}{l}\left( {ABB'A'} \right) \cap \left( {ABC} \right) = AB\\B'K \subset \left( {ABB'A'} \right),\,\,B'K \bot AB\\HK \subset \left( {ABC} \right),\,\,HK \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {ABB'A'} \right);\left( {ABC} \right)} \right) = \angle \left( {B'K;HK} \right) = \angle B'HK = {45^0}\).
\( \Rightarrow \Delta B'HK\) vuông cân tại \(H \Rightarrow B'H = HK = x\).
Xét tam giác vuông \(BB'H\) có: \(BH = \sqrt {BB{'^2} - BH{'^2}} = \sqrt {4{a^2} - {x^2}} \).
Xét tam giác vuông \(ABC\) có: \(AC = BC.\sin {60^0} = a\sqrt 3 \), \(AB = BC.\cos {60^0} = a\).
Áp dụng định lí Ta-lét ta có: \(\dfrac{{BH}}{{BC}} = \dfrac{{HK}}{{AC}} \Rightarrow \dfrac{{\sqrt {4{a^2} - {x^2}} }}{{2a}} = \dfrac{x}{{a\sqrt 3 }}\)
\(\begin{array}{l} \Leftrightarrow 3\left( {4{a^2} - {x^2}} \right) = 4{x^2}\\ \Leftrightarrow 12{a^2} - 3{x^2} = 4{x^2}\\ \Leftrightarrow {x^2} = \dfrac{{12{a^2}}}{7}\\ \Leftrightarrow x = \dfrac{{2a\sqrt {21} }}{7} = B'H\end{array}\)
\({S_{\Delta ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.a.a\sqrt 3 = \dfrac{{{a^2}\sqrt 3 }}{2}\).
Vậy \({V_{ABC.A'B'C'}} = B'H.{S_{\Delta ABC}} = \dfrac{{2a\sqrt {21} }}{7}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{3{a^3}\sqrt 7 }}{7}\).
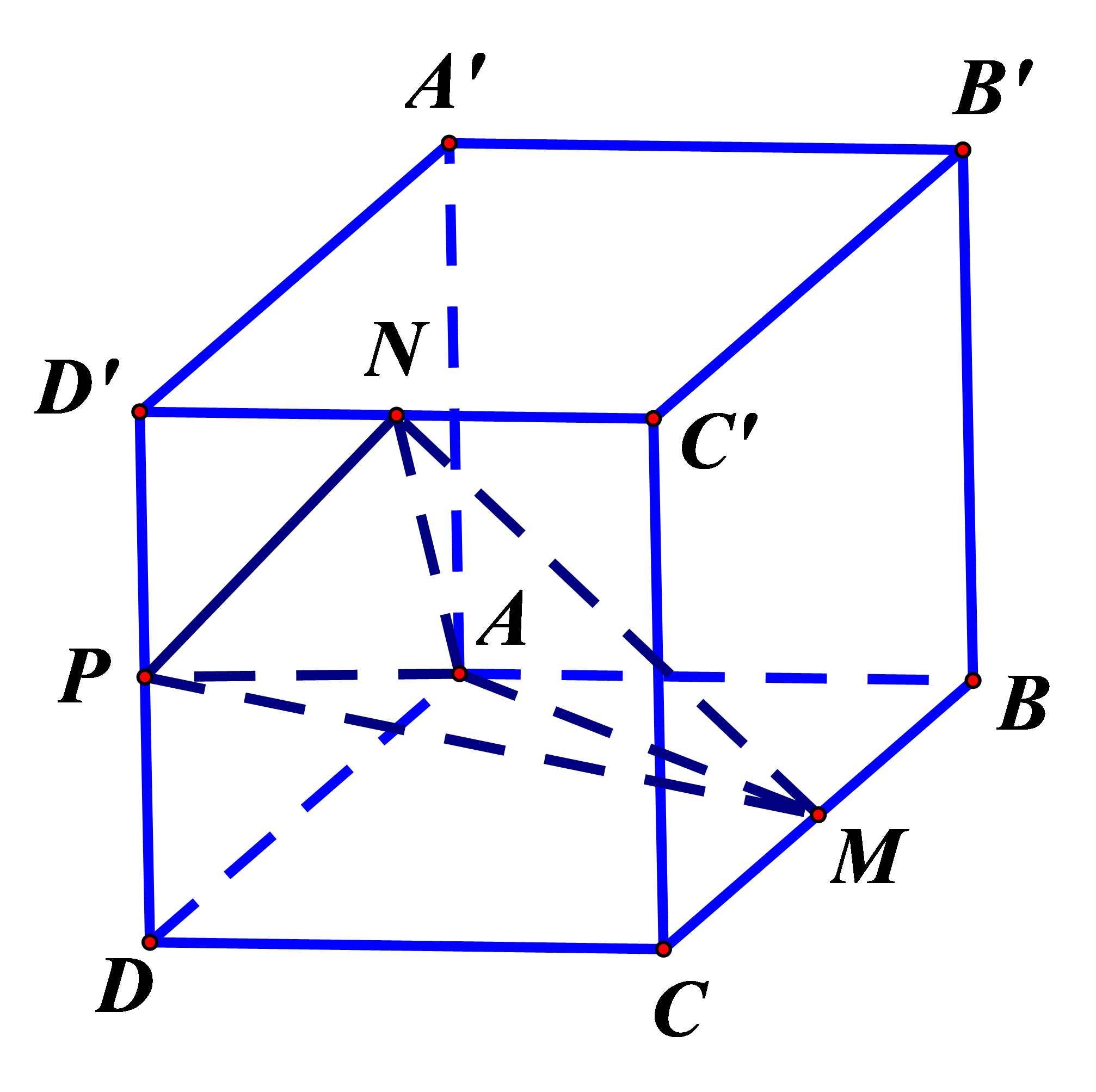
Cho hình hộp chữ nhật $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ có $M, N, P$ lần lượt là trung điểm các cạnh $B C, C^{\prime} D^{\prime}, D D^{\prime}$ (tham khảo hình vẽ). Biết thể tích khối hộp bằng 144 , thể tích khối tứ diện $A M N P$ bằng
15
15
15
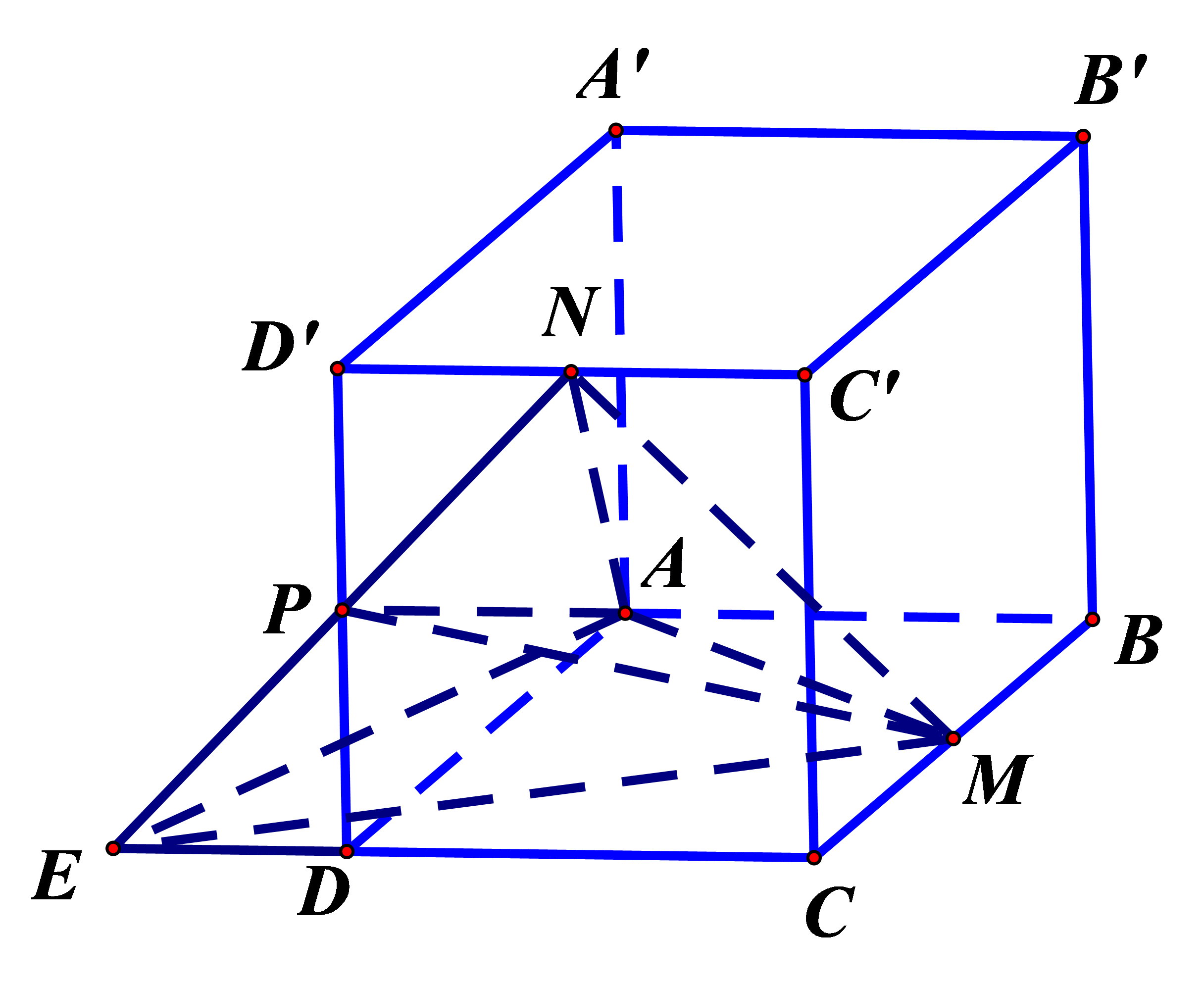
Bước 1: Gọi $E=N P \cap C D$. Đặt $D C=2 d, B C=2 r$
Gọi $E=N P \cap C D$. Đặt $D C=2 d, B C=2 r$
Ta có:
\(\begin{array}{l}{S_{EMA}} = {S_{ECBA}} - {S_{EMC}} - {S_{ABM}}\\ = 5dr - \dfrac{3}{2}dr - dr = \dfrac{5}{2}dr\end{array}\)
Bước 2: Tính thể tích của NPAM
\(\begin{array}{l}{V_{NEAM}} = \dfrac{1}{3}{S_{EMA}} \cdot d(N,(EMA))\\ = \dfrac{1}{3}{S_{EMA}} \cdot CC' = \dfrac{5}{{24}} \cdot 4dr \cdot C{C^\prime }\\ = \dfrac{5}{{24}}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}} = 30.\\ \Rightarrow {V_{NPAM}} = \dfrac{1}{2}{V_{NEAM}} = 15\end{array}\)
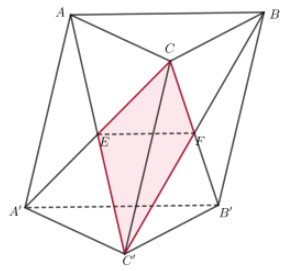
Cho khối lăng trụ tam giác đều ABC.A′B′C′. Các mặt phẳng (ABC′) và (A′B′C) chia khối lăng trụ đã cho thành 4 khối đa diện. Kí hiệu H1, H2 lần lượt là khối có thể tích lớn nhất và nhỏ nhất trong bốn khối trên. Giá trị của \(\dfrac{{{V_{\left( {{H_1}} \right)}}}}{{{V_{\left( {{H_2}} \right)}}}}\) bằng
 s
s
Bước 1:
Gọi \(E\) là giao điểm của AC và AC’ và F là giao điểm của BC’ và B’C’
Khi đó (ABC’) và (A’B’C) chia khối lăng trụ tam giác đều ABC.A’B’C’ thành 4 khối đa diện: CEFC’;FEA’B’C’;FEABC và FEABB’A’
Gọi V là thể tích của khối lăng trụ tam giác đều ABC.A’B’C’.
Bước 2: Tính thể tích của $CEFC’;FEA’B’C’;FEABC$ và $FEABB’A'$ theo thể tích của $ABC.A'B'C'$
Ta có \({V_{C.A'B'C'}} = {V_{C'.ABC}} = \dfrac{1}{3}V\)
\({V_{FEA'B'C'}} = {V_{C.A'B'C'}} - {V_{CEFC'}}\) và \({V_{FEABC}} = {V_{C'.ABC}} - {V_{CEFC'}}\)
\( \Rightarrow {V_{FEA'B'C'}} = {V_{FEABC}}\)
Mặt khác
\(\begin{array}{l}\dfrac{{{V_{CEFC'}}}}{{V_{C.A'B'C'}}} = \dfrac{{CE}}{{CA}}.\dfrac{{CF}}{{CB'}} = \dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}\\ \Rightarrow {V_{CEFC'}} = \dfrac{1}{4}{V_{C.A'B'C'}} = \dfrac{1}{4}.\dfrac{1}{3}V = \dfrac{1}{{12}}V\end{array}\)
\( \Rightarrow {V_{FEA'B'C'}} = {V_{FEABC}}\)\( = {V_{C.A'B'C'}} - {V_{CEFC'}}\)\( = \dfrac{1}{3}V - \dfrac{1}{{12}}V = \dfrac{1}{4}V\)
\( \Rightarrow {V_{FEABB'A'}} = V - 2.\dfrac{1}{4}V - \dfrac{1}{{12}}V = \dfrac{5}{{12}}V\)
Do đó \({H_1}\) có thể tích lớn nhất là khối đa diện FEABB’A’; \({H_2}\) có thể tích nhỏ nhất là khối đa diện CEFC’ và \(\dfrac{{{V_{\left( {{H_1}} \right)}}}}{{{V_{\left( {{H_2}} \right)}}}} = 5\).
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\)có \(AB = a,\) đường thẳng \(A'B\) tạo với mặt phẳng \(\left( {BCC'B'} \right)\) một góc \({30^0}.\) Tính thể tích khối lăng trụ \(ABC.A'B'C'.\)
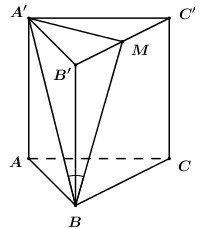
Gọi \(M\) là trung điểm của \(B'C'\). Vì \(\Delta A'B'C'\) đều nên \(A'M \bot B'C'\).
Ta có: \(\left\{ \begin{array}{l}A'M \bot B'C'\\A'M \bot BB'\,\,\left( {BB' \bot \left( {A'B'C'} \right)} \right)\end{array} \right.\) \( \Rightarrow A'M \bot \left( {BCC'B'} \right)\).
\( \Rightarrow BM\) là hình chiếu của \(A'M\) lên \(\left( {BCC'B'} \right)\) \( \Rightarrow \angle \left( {A'B;\left( {BCC'B'} \right)} \right) = \angle \left( {A'B;MB} \right) = \angle A'BM = {30^0}\).
Theo bài ra ta có \(\Delta A'B'C'\) đều cạnh \(a\) nên \(A'M = \dfrac{{a\sqrt 3 }}{2}\) và \({S_{\Delta A'B'C'}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Ta có: \(A'M \bot \left( {BCC'B'} \right) \Rightarrow A'M \bot BM\) \( \Rightarrow \Delta A'BM\) vuông tại \(M\) \( \Rightarrow BM = A'M.\cot {30^0} = \dfrac{{3a}}{2}\).
Áp dụng định lí Pytago trong tam giác vuông \(BB'M\) ta có: \(BB' = \sqrt {B{M^2} - BB{'^2}} = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = a\sqrt 2 \).
Vậy \({V_{ABC.A'B'C'}} = BB'.{S_{A'B'C'}} = a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{4}\).
Cho hình lập phương \(ABCD.A'B'C'D'\) có thể tích \(V\). Gọi \(M\) là điểm thuộc cạnh \(BB'\) sao cho \(MB = 2MB'\). Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\) và vuông góc với \(AC'\) cắt các cạnh \(DD'\), \(DC\), \(BC\) lần lượt tại \(N\), \(P\), \(Q\). Gọi \({V_1}\) là thể tích của khối đa diện \(CPQMNC'\).Tính tỉ số \(\dfrac{{{V_1}}}{V}\).
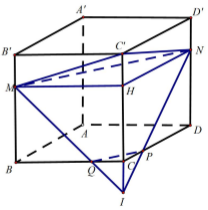
Gọi cạnh của hình lập phương là \(a\).
Ta có:
\(\left( \alpha \right) \bot AC'\)\( \Rightarrow \left( \alpha \right)\parallel BD\). Trong \(\left( {BDD'B'} \right)\) kẻ \(MN\parallel BD\,\,\left( {N \in DD'} \right)\).
\(\left( \alpha \right) \bot AC' \Rightarrow \alpha \parallel B'C\). Trong \(\left( {BCC'B'} \right)\) kẻ \(MQ\parallel B'C\,\,\left( {Q \in BC} \right)\).
\(\left( \alpha \right) \bot AC'\)\( \Rightarrow \left( \alpha \right)\parallel BD\). Trong \(\left( {BDD'B'} \right)\) kẻ \(MN\parallel BD\,\,\left( {N \in DD'} \right)\).
\(\left( \alpha \right) \bot AC' \Rightarrow \alpha \parallel B'C\). Trong \(\left( {ABCD} \right)\) kẻ \(PQ\parallel BD\,\,\left( {P \in DC} \right)\).
Khi đó \(\left( \alpha \right) \equiv \left( {MNPQ} \right)\).
Theo cách dựng ta có \(BQ = 2QC,\,\,DP = 2PC,\,\,DN = 2ND'\).
Gọi \(H\) là điểm thuộc \(CC'\) sao cho \(CH = 2HC'\).
Khi đó ta có: \({V_{CPQMNC'}} = {V_{C.MHN}} + {V_{CQP.MHN}}\).
Xét hình chóp \(C'.MHN\) có \(C'H = \dfrac{a}{3}\), \({S_{\Delta MHN}} = \dfrac{1}{2}{a^2}\).
\( \Rightarrow {V_{C'.MHN}} = \dfrac{1}{3}C'H.{S_{\Delta MHN}} = \dfrac{1}{3}.\dfrac{a}{3}.\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}}}{{18}} = \dfrac{V}{{18}}\).
Xét hình chóp cụt \(CQP.MHN\) có
\(\begin{array}{l}{V_{CQP.MHN}} = {V_{I.MHN}} - {V_{I.CQP}} = \dfrac{1}{3}\left( {IH.{S_{\Delta MHN}} - IC.{S_{\Delta CQP}}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{3}\left( {a.\dfrac{1}{2}{a^2} - \dfrac{a}{3}.\dfrac{1}{2}.\dfrac{a}{3}.\dfrac{a}{3}} \right) = \dfrac{{13{a^3}}}{8} = \dfrac{{13V}}{{81}}\end{array}\)
\( \Rightarrow {V_1} = {V_{CPQMNC'}} = {V_{C.MHN}} + {V_{CQP.MHN}} = \dfrac{V}{{18}} + \dfrac{{13V}}{{81}} = \dfrac{{35V}}{{162}}\).
Vậy \(\dfrac{{{V_1}}}{V} = \dfrac{{35}}{{162}}\)
Cho lăng trụ đều \(ABC.A'B'C'\), cạnh đáy bằng a, góc giữa hai mặt phẳng \(\left( {A'BC} \right)\) và \(\left( {ABC} \right)\) bằng \(60^\circ \). Tính thể tích khối lăng trụ đó.
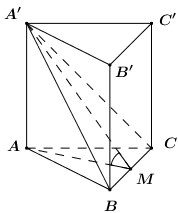
Gọi \(M\) là trung điểm của \(BC\). Ta có:
\(AM \bot BC\) (do \(\Delta ABC\) đều)
\(BC \bot AA'\,\,\left( {gt} \right)\)
\( \Rightarrow BC \bot \left( {AA'M} \right) \Rightarrow BC \bot A'M\).
Ta có: \(\left\{ \begin{array}{l}\left( {A'BC} \right) \cap \left( {ABC} \right) = BC\\AM \subset \left( {ABC} \right),\,\,AM \bot BC\\A'M \subset \left( {A'BC} \right),\,\,A'M \bot BC\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {A'BC} \right);\left( {ABC} \right)} \right) = \angle \left( {A'M;AM} \right) = \angle A'MA = {60^0}\).
Vì \(\Delta ABC\) đều cạnh \(a\) nên \(AM = \dfrac{{a\sqrt 3 }}{2}\) và \({S_{\Delta ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\).
Xét tam giác vuông \(A'AM\) có: \(AA' = AM.\tan {60^0} = \dfrac{{a\sqrt 3 }}{2}.\sqrt 3 = \dfrac{{3a}}{2}\).
Vậy thể tích khối lăng trụ là \({V_{ABC.A'B'C'}} = AA'.{S_{\Delta ABC}} = \dfrac{{3a}}{2}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{a^2}\sqrt 3 }}{8}\).
Đề thi THPT QG - 2021 - mã 101
Cho khối hộp chữ nhật \(ABCD.A'B'C'D'\) có đáy là hình vuông, \(BD = 2a,\) góc giữa hai mặt phẳng \(\left( {A'B{\rm{D}}} \right)\) và \(\left( {ABCD} \right)\) bằng \({30^0}\). Thể tích của khối hộp chữ nhật đã cho bằng
* Xác định \(\angle \left( {\left( {A'BD} \right);\left( {ABCD} \right)} \right)\).
+ \(\left( {A'BC} \right) \cap \left( {ABCD} \right) = BD\).
+ \(\left\{ \begin{array}{l}AA' \bot BD\\AO \bot BD\end{array} \right. \Rightarrow \left( {A'AO} \right) \bot BD\).
+ \(\left\{ \begin{array}{l}\left( {A'AO} \right) \cap \left( {A'BD} \right) = A'O\\\left( {A'AO} \right) \cap \left( {ABCD} \right) = AO\end{array} \right.\)
\( \Rightarrow \angle \left( {\left( {A'BD} \right);\left( {ABCD} \right)} \right) = \angle \left( {A'O;AO} \right) = \angle A'OA\).
\( \Rightarrow \angle A'OA = {30^0}\).
* Xét tam giác \(A'OA\) vuông tại \(A\) có \(AO = \dfrac{1}{2}AC = \dfrac{1}{2}BD = a\).
\( \Rightarrow AA' = \tan {30^0}.AO = \dfrac{{a\sqrt 3 }}{3}\).
\( \Rightarrow {V_{ABCD.A'B'C'D'}} = {S_{ABCD}}.AA' = \dfrac{1}{2}AC.BD.AA'\) \( = \dfrac{1}{2}.{\left( {2a} \right)^2}.\dfrac{{a\sqrt 3 }}{3} = \dfrac{{2\sqrt 3 {a^3}}}{3}\).
Cho khối lăng trụ \(ABC.A'B'C'\). Gọi \(E\) là trọng tâm tam giác \(A'B'C'\) và \(F\) là trung điểm \(BC\). Gọi \({V_1}\) là thể tích khối chóp \(B'.EAF\) và \({V_2}\) là thể tích khối lăng trụ \(ABC.A'B'C'\). Khi đó \(\dfrac{{{V_1}}}{{{V_2}}}\) có giá trị bằng
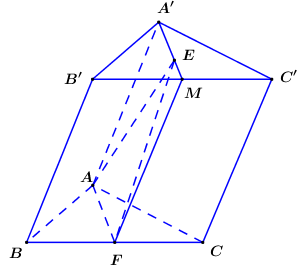
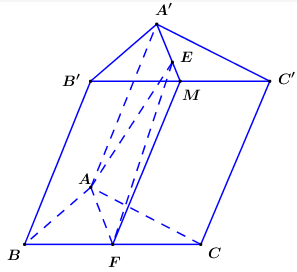
Gọi thể tích $ABC.A'B'C'$ là $V$.
Gọi \(M\) là trung điểm của \(B'C'\) ta có: \({S_{\Delta AEF}} = \dfrac{1}{2}{S_{AA'MF}}\) \( \Rightarrow {V_{B'.AEF}} = \dfrac{1}{2}{V_{B'.AA'MF}}\).
Mà \({V_{B'.AA'MF}} = \dfrac{2}{3}{V_{ABF.A'B'M}} = \dfrac{2}{3}.\dfrac{1}{2}V = \dfrac{1}{3}V\).
\( \Rightarrow {V_{B'.AEF}} = \dfrac{1}{2}{V_{B'.AA'MF}} = \dfrac{1}{2}.\dfrac{1}{3}V = \dfrac{1}{6}V\).
Vậy \(\dfrac{{{V_1}}}{V} = \dfrac{1}{6}\).
Cho hình lăng trụ tam giác \(ABC.A'B'C'\) có diện tích đáy bằng \(12\) và chiều cao bằng \(6\). Gọi \(M,\,\,N\) lần lượt là trung điểm của \(CB,\,\,CA\) và \(P,\,\,Q,\,\,R\) lần lượt là tâm các hình bình hành \(ABB'A'\), \(BCC'B'\), \(CAA'C'\). Thể tích của khối đa diện \(PQRABMN\) bằng:
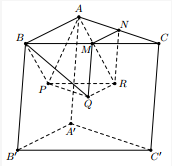
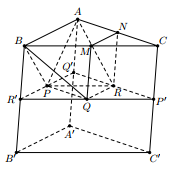
Gọi \(P',\,\,Q',\,\,R'\) lần lượt là giao điểm của mặt phẳng \(\left( {PQR} \right)\) với các cạnh \(CC',\,\,AA',\,\,BB'\).
Dễ dàng chứng minh được \(P',\,\,Q',\,\,R'\) tương ứng là trung điểm của các cạnh \(CC',\,\,AA',\,\,BB'\), đồng thời \(P,\,\,Q,\,\,R\) lần lượt là trung điểm của các cạnh \(Q'R',\,\,R'P',\,\,P'Q'\).
Đặt \(V = {V_{ABC.Q'R'P'}}\).
Ta có: \({S_{R'PQ}} = \dfrac{1}{4}{S_{R'Q'P'}}\) nên \({V_{B.R'PQ}} = \dfrac{1}{4}{V_{B.R'Q'P'}} \)\(= \dfrac{1}{4}.\dfrac{1}{3}V = \dfrac{1}{{12}}V\)
Tương tự ta có: \({V_{A.Q'PR}} = \dfrac{1}{{12}}V\).
Ta có: \({S_{MNC}} = {S_{QRP'}} = \dfrac{1}{4}{S_{ABC}}\) nên \({V_{CMN.P'QR}} = \dfrac{V}{4}\)
Vậy \(V{V_{PQRABMN}} = V - {V_{B.R'PQ}} - {V_{A.Q'PR}} - {V_{CMN.P'QR}} = V - 2.\dfrac{V}{{12}} - \dfrac{V}{4} = \dfrac{{7V}}{{12}} = \dfrac{7}{2}.\dfrac{1}{2}.12.6 = 21\).
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có độ dài cạnh đáy \(AB = 8,\) cạnh bên bằng \(\sqrt 6 \) (minh họa như hình vẽ). Gọi \(M\) là trung điểm của cạnh \(A'C'\). Khoảng cách từ \(B'\) đến mặt phẳng \(\left( {ABM} \right)\) bằng bao nhiêu?
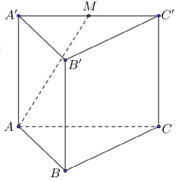
Đáp án: $d\left(B^{\prime},(A B M)\right)$
Đáp án: $d\left(B^{\prime},(A B M)\right)$
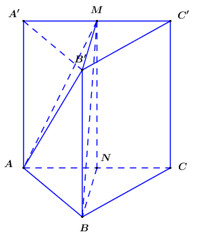
Bước 1: Gọi \(N\) là trung điểm của \(AC\), chứng minh \(d\left( {A;\left( {BB'M} \right)} \right) = d\left( {A;\left( {BB'MN} \right)} \right) = AN\).
Gọi \(N\) là trung điểm của \(AC\) ta có \(\left( {BB'M} \right) \equiv \left( {BB'MN} \right)\) nên \(d\left( {A;\left( {BB'M} \right)} \right) = d\left( {A;\left( {BB'MN} \right)} \right)\).
Vì tam giác ABC đều nên \(AN \bot BN\). Ta có \(\left\{ \begin{array}{l}AN \bot BN\\AN \bot MN\end{array} \right. \Rightarrow AN \bot \left( {BB'MN} \right)\) nên \(d\left( {A;\left( {BB'MN} \right)} \right) = AN = 4\)
Bước 2: Tính \({V_{A.BB'M}} = \dfrac{1}{3}d\left( {A;\left( {BB'MN} \right)} \right).{S_{\Delta BB'M}} = {V_{B'.ABM}}\).
Ta lại có \(BN = \dfrac{{AB\sqrt 3 }}{2} = 4\sqrt 3 ,\,\,MN = AA' = \sqrt 6 \) nên \({S_{BB'MN}} = MN.BN = \sqrt 6 .4\sqrt 3 = 12\sqrt 2 \) \( \Rightarrow {S_{\Delta BB'M}} = 6\sqrt 2 \).
\( \Rightarrow {V_{A.BB'M}} = \dfrac{1}{3}d\left( {A;\left( {BB'MN} \right)} \right).{S_{\Delta BB'M}} = \dfrac{1}{3}.4.12\sqrt 2 = 16\sqrt 2 = {V_{B'.ABM}}\)
Bước 3: Sử dụng \(d\left( {B';\left( {ABM} \right)} \right) = \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}}\).
Lại có \({V_{B'.ABM}} = \dfrac{1}{3}d\left( {B';\left( {ABM} \right)} \right).{S_{\Delta ABM}}\) nên \(d\left( {B';\left( {ABM} \right)} \right) \)\(= \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}}\).
Ta có:
\(\begin{array}{l}AM = \sqrt {A'{A^2} + A'{M^2}} \\= \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {4^2}} = \sqrt {22} \\AB = 8\\BM = \sqrt {BB{'^2} + B'{M^2}} \\= \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {{\left( {4\sqrt 3 } \right)}^2}} = 3\sqrt 6 \end{array}\)
Bước 4: Sử dụng công thức \({S_{\Delta ABM}} = \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} \) với \(p\) là nửa chu vi tam giác \(ABM\).
Gọi \(p\) là nửa chu vi tam giác ABM ta có \(p = \dfrac{{\sqrt {22} + 8 + 3\sqrt 6 }}{2}\).
\( \Rightarrow {S_{\Delta ABM}} \)\(= \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} \)\( = 12\sqrt 2 \)
Vậy \(d\left( {B';\left( {ABM} \right)} \right) = \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}} = \dfrac{{3.16\sqrt 2 }}{{12\sqrt 2 }} = 4\).
Ông A dự định sử dụng hết 5m2 kính để làm một bể cá bằng kính có dạng hình hộp chữ nhật không nắp, chiều dài gấp đôi chiều rộng (các mối ghép có kích thước không đáng kể). Bể cá có dung tích lớn nhất bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
Đáp án:
$m^3$
Đáp án:
$m^3$
Bước 1: Gọi chiều rộng bể cá là x, tính chiều dài và chiều cao của bế cá theo x.
Gọi chiều rộng của bể cá là x (m) \(\left( {x > 0} \right) \Rightarrow \) Chiều dài của bể cá là \(2x\,\,\left( m \right)\)
Gọi h là chiều cao của bể cá ta có \(2{x^2} + 2xh + 4xh = 5 \Leftrightarrow 2{x^2} + 6xh = 5 \Leftrightarrow h = \dfrac{{5 - 2{x^2}}}{{6x}}\)
Bước 2: Tính thể tích của bể cá theo x, sử dụng phương pháp hàm số tìm GTLN của thể tích bể cá.
Khi đó thể tích của bể cá là \(2{x^2}.\dfrac{{5 - 2{x^2}}}{{6x}} = \dfrac{1}{3}\left( {5x - 2{x^3}} \right) = \dfrac{1}{3}f\left( x \right)\)
Xét hàm số \(f\left( x \right) = 5x - 2{x^3}\,\,\left( {x > 0} \right)\) có \(f'\left( x \right) = 5 - 6{x^2} = 0 \Leftrightarrow x = \sqrt {\dfrac{5}{6}} \)
Lập BBT:
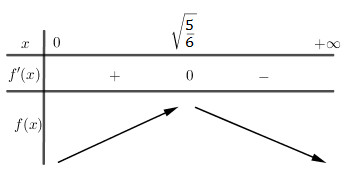
\( \Rightarrow \mathop {\max }\limits_{\left( {0; + \infty } \right)} f\left( x \right) = f\left( {\sqrt {\dfrac{5}{6}} } \right)\)
\( \Rightarrow {V_{\max }} = \dfrac{1}{3}f\left( {\sqrt {\dfrac{5}{6}} } \right) = \dfrac{{5\sqrt {50} }}{{27}} \approx 1,01{m^3}\)
Cho hình hộp $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ có đáy $A B C D$ là hình thoi cạnh $a$, $\widehat{B C D}=120^{\circ} .$ Biết rằng hình chiếu vuông góc của $A^{\prime}$ lên mặt phẳng $(A B C D)$ trùng với giao điểm của $A C$ và $B D$. Diện tích tam giác $A^{\prime} A B$ bằng $\dfrac{a^{2} \sqrt{3}}{4}$
Tính góc giữa hai mặt phẳng $\left(A B B^{\prime} A^{\prime}\right)$ và $(A B C)$
Bước 1: Tính diện tích tam giác ABH
Hình thoi $A B C D$ có $\widehat{B C D}=120^{\circ}$
$\Rightarrow \widehat{A B C}=60^{\circ}$
Do đó $A B C$ là tam giác đều
$\Rightarrow S_{A B C}=\dfrac{a^{2} \sqrt{3}}{4}$
$\Rightarrow S_{A B H}=\dfrac{1}{2} S_{A B C}=\dfrac{a^{2} \sqrt{3}}{8} .$
Bước 2: Sử dụng công thức liên hệ giữa diện tích hình chiếu của đa giác và đa giác ban đầu.
Tam giác $A B H$ là hình chiếu của tam giác $A^{\prime} B H$
Gọi góc giữa $\left(A B B^{\prime} A^{\prime}\right)$ và $(A B C D)$ là $\varphi$
Khi đó ta có $S_{A B H}=S_{A B A^{\prime}} \cos \varphi \Rightarrow \cos \varphi=\dfrac{S_{A B H}}{S_{A B A^{\prime}}}=\dfrac{1}{2} \Rightarrow \varphi=60^{\circ}$
Cho hình hộp $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ có đáy $A B C D$ là hình thoi cạnh $a$, $\widehat{B C D}=120^{\circ} .$ Biết rằng hình chiếu vuông góc của $A^{\prime}$ lên mặt phẳng $(A B C D)$ trùng với giao điểm của $A C$ và $B D$. Diện tích tam giác $A^{\prime} A B$ bằng $\dfrac{a^{2} \sqrt{3}}{4}$
Tính thể tích khối lăng trụ $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$
Bước 1: Gọi $M$ là trung điểm $A B, I$ là trung điểm $A M$. Tính góc A’IH
Ta có $S_{A B C D}=2 S_{A B C}=\dfrac{a^{2} \sqrt{3}}{2}$
Gọi $M$ là trung điểm $A B, I$ là trung điểm $A M$
Khi đó $H I \perp A B \Rightarrow$ góc giữa $\left(A B B^{\prime} A^{\prime}\right)$ và $(A B C D)$ là góc $\widehat{A^{\prime} I H}=60^{\circ}$
Bước 2: Tính $V_{A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}$
Ta có $I H=\dfrac{1}{2} C M=\dfrac{a \sqrt{3}}{4} \Rightarrow A^{\prime} H\\=I H \cdot \tan 60^{\circ}=\dfrac{3 a}{4}$
$\Rightarrow V_{A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}=A^{\prime} H \cdot S_{A B C D}\\=\dfrac{3 a}{4} \cdot \dfrac{a^{2} \sqrt{3}}{2}=\dfrac{3 a^{3} \sqrt{3}}{8} .$

