Câu hỏi:
2 năm trước
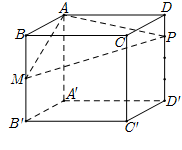
Cho hình hộp chữ nhật $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ có $M, N, P$ lần lượt là trung điểm các cạnh $B C, C^{\prime} D^{\prime}, D D^{\prime}$ (tham khảo hình vẽ). Biết thể tích khối hộp bằng 144 , thể tích khối tứ diện $A M N P$ bằng
Trả lời bởi giáo viên
Đáp án đúng:
15
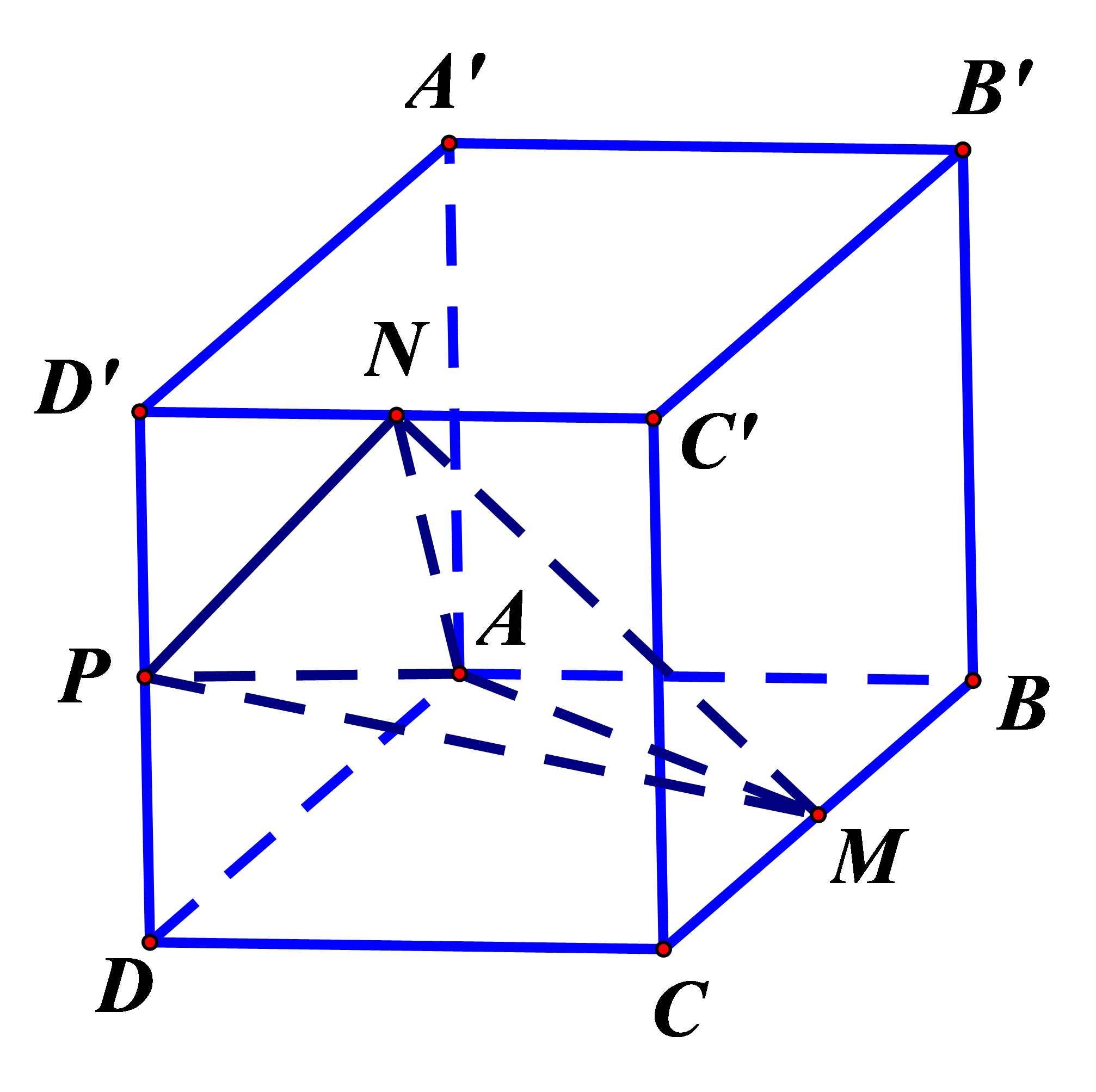
Bước 1: Gọi $E=N P \cap C D$. Đặt $D C=2 d, B C=2 r$
Gọi $E=N P \cap C D$. Đặt $D C=2 d, B C=2 r$
Ta có:
\(\begin{array}{l}{S_{EMA}} = {S_{ECBA}} - {S_{EMC}} - {S_{ABM}}\\ = 5dr - \dfrac{3}{2}dr - dr = \dfrac{5}{2}dr\end{array}\)
Bước 2: Tính thể tích của NPAM
\(\begin{array}{l}{V_{NEAM}} = \dfrac{1}{3}{S_{EMA}} \cdot d(N,(EMA))\\ = \dfrac{1}{3}{S_{EMA}} \cdot CC' = \dfrac{5}{{24}} \cdot 4dr \cdot C{C^\prime }\\ = \dfrac{5}{{24}}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}} = 30.\\ \Rightarrow {V_{NPAM}} = \dfrac{1}{2}{V_{NEAM}} = 15\end{array}\)
Hướng dẫn giải:
Bước 1: Gọi $E=N P \cap C D$. Đặt $D C=2 d, B C=2 r$
Biểu diễn $ S_{E M A}$ theo d và r.
Bước 2: Tính thể tích của NPAM
