Câu hỏi:
2 năm trước
Cho khối lăng trụ \(ABC.A'B'C'\). Gọi \(E\) là trọng tâm tam giác \(A'B'C'\) và \(F\) là trung điểm \(BC\). Gọi \({V_1}\) là thể tích khối chóp \(B'.EAF\) và \({V_2}\) là thể tích khối lăng trụ \(ABC.A'B'C'\). Khi đó \(\dfrac{{{V_1}}}{{{V_2}}}\) có giá trị bằng
Trả lời bởi giáo viên
Đáp án đúng: c
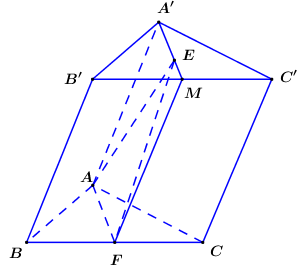
Gọi thể tích $ABC.A'B'C'$ là $V$.
Gọi \(M\) là trung điểm của \(B'C'\) ta có: \({S_{\Delta AEF}} = \dfrac{1}{2}{S_{AA'MF}}\) \( \Rightarrow {V_{B'.AEF}} = \dfrac{1}{2}{V_{B'.AA'MF}}\).
Mà \({V_{B'.AA'MF}} = \dfrac{2}{3}{V_{ABF.A'B'M}} = \dfrac{2}{3}.\dfrac{1}{2}V = \dfrac{1}{3}V\).
\( \Rightarrow {V_{B'.AEF}} = \dfrac{1}{2}{V_{B'.AA'MF}} = \dfrac{1}{2}.\dfrac{1}{3}V = \dfrac{1}{6}V\).
Vậy \(\dfrac{{{V_1}}}{V} = \dfrac{1}{6}\).
Hướng dẫn giải:
- Gọi thể tích $ABC.A'B'C'$ là $V$.
- So sánh \({V_{B'.AEF}},\,\,{V_{B'.AA'MF}}\).
- So sánh \({V_{B'.AA'MF}},\,\,{V_{ABF.A'B'M}}\), từ đó so sánh \({V_{B'.AA'MF}},\,\,V\).
