Câu hỏi:
2 năm trước
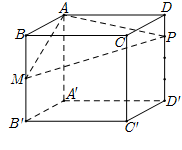
Cho hình hộp $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$ có đáy $A B C D$ là hình thoi cạnh $a$, $\widehat{B C D}=120^{\circ} .$ Biết rằng hình chiếu vuông góc của $A^{\prime}$ lên mặt phẳng $(A B C D)$ trùng với giao điểm của $A C$ và $B D$. Diện tích tam giác $A^{\prime} A B$ bằng $\dfrac{a^{2} \sqrt{3}}{4}$
Tính thể tích khối lăng trụ $A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}$
Trả lời bởi giáo viên
Đáp án đúng: b
Bước 1: Gọi $M$ là trung điểm $A B, I$ là trung điểm $A M$. Tính góc A’IH
Ta có $S_{A B C D}=2 S_{A B C}=\dfrac{a^{2} \sqrt{3}}{2}$
Gọi $M$ là trung điểm $A B, I$ là trung điểm $A M$
Khi đó $H I \perp A B \Rightarrow$ góc giữa $\left(A B B^{\prime} A^{\prime}\right)$ và $(A B C D)$ là góc $\widehat{A^{\prime} I H}=60^{\circ}$
Bước 2: Tính $V_{A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}$
Ta có $I H=\dfrac{1}{2} C M=\dfrac{a \sqrt{3}}{4} \Rightarrow A^{\prime} H\\=I H \cdot \tan 60^{\circ}=\dfrac{3 a}{4}$
$\Rightarrow V_{A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}=A^{\prime} H \cdot S_{A B C D}\\=\dfrac{3 a}{4} \cdot \dfrac{a^{2} \sqrt{3}}{2}=\dfrac{3 a^{3} \sqrt{3}}{8} .$
Hướng dẫn giải:
Bước 1: Gọi $M$ là trung điểm $A B, I$ là trung điểm $A M$. Tính góc A’IH
Bước 2: Tính $V_{A B C D \cdot A^{\prime} B^{\prime} C^{\prime} D^{\prime}}$
