Giải bất phương trình $\log_{2}\left( {3x-1} \right) \ge 3$.
Điều kiện: $x > \dfrac{1}{3}$
BPT $ \Leftrightarrow 3x - 1 \ge 8 \Leftrightarrow x \ge 3$
Kết hợp điều kiện ta được $x \ge 3$
Giải bất phương trình \({\log _{\frac{1}{3}}}(x + {9^{500}}) > - 1000\)
Điều kiện $x + {9^{500}} > 0 \Leftrightarrow x > - {9^{500}}$
Vì ${\rm{0 < a}} = \dfrac{1}{3} < 1$ nên
$\begin{array}{l}{\log _{\dfrac{1}{3}}}\left( {x + {9^{500}}} \right) > - 1000 \Leftrightarrow 0 < x + {9^{500}} < {\left( {\dfrac{1}{3}} \right)^{ - 1000}} \Leftrightarrow 0 < x + {9^{500}} < {3^{1000}}\\ \Leftrightarrow - {9^{500}} < x < {3^{1000}} - {9^{500}} \Leftrightarrow - {3^{1000}} < x < {3^{1000}} - {3^{1000}} \Leftrightarrow - {3^{1000}} < x < 0\end{array}$
Số nguyên nhỏ nhất thỏa mãn $\log_{2}\left( {5x-3} \right) > 5$ là:
Điều kiện: $x > \dfrac{3}{5}$
${\log _2}\left( {5x - 3} \right) > 5 \Leftrightarrow 5x - 3 > {2^5} \Leftrightarrow 5x > 35 \Leftrightarrow x > 7$
Vậy số nguyên nhỏ nhất thỏa mãn bất phương trình là \(x = 8\).
Tìm tập nghiệm \(S\) của bất phương trình \({\log _{\frac{1}{2}}}\left( {x - 1} \right) > {\log _{\frac{1}{2}}}\left( {5 - 2x} \right)\).
Điều kiện \(\left\{ \begin{array}{l}x - 1 > 0\\5 - 2x > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > 1\\x < \dfrac{5}{2}\end{array} \right.\)
\({\log _{\frac{1}{2}}}\left( {x - 1} \right) > {\log _{\frac{1}{2}}}\left( {5 - 2x} \right) \Leftrightarrow x - 1 < 5 - 2x \Leftrightarrow x < 2\).
Kết hợp với điều kiện suy ra $S= (1;2)$.
Tìm tất cả các giá trị thực của tham số \(m\) để bất phương trình \(4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0\) nghiệm đúng với mọi giá trị \(x \in \left[ {1;64} \right]\).
Điều kiện : $x > 0$
\(4.{\left( {{{\log }_2}\sqrt x } \right)^2} + {\log _2}x + m \ge 0 \Leftrightarrow 4.{\left( {{{\log }_2}\sqrt x } \right)^2} + 2.{\log _2}\sqrt x \ge - m\)(1)
Đặt \(t = {\log _2}\sqrt x \). Khi \(x \in \left[ {1;64} \right] \Rightarrow t \in \left[ {0;3} \right]\).
Ta có bất phương trình \(4{t^2} + 2t \ge - m\).
Xét \(f(t) = 4{t^2} + 2t;f'(t) = 8t + 2 > 0,\forall t \in \left[ {0;3} \right]\)
Để (1) nghiệm đúng với \(\forall t \in \left[ {0;3} \right]\) thì $\mathop {\min }\limits_{\left[ {0;3} \right]} f\left( t \right) \ge - m$
\( \Leftrightarrow f(0) \ge - m \Leftrightarrow 0 \ge - m \Leftrightarrow m \ge 0\).
Tập nghiệm của bất phương trình $\ln\left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0$ là:
$\begin{array}{l}\ln \left[ {\left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1} \right] > 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) + 1 > 1\\ \Leftrightarrow \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right) > 0\end{array}$
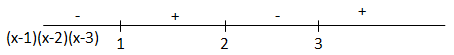
$ \Rightarrow x \in (1;2) \cup (3; + \infty )$
Tập nghiệm của bất phương trình $\log\left( {{x^2} + 25} \right) > \log\left( {10x} \right)$ là:
Điều kiện: $x > 0$
$\log ({x^2} + 25) > \log (10x) \Leftrightarrow {x^2} + 25 > 10x \Leftrightarrow {(x - 5)^2} > 0 \Leftrightarrow x \ne 5$
Tập nghiệm của bất phương trình là: $(0;5) \cup (5; + \infty )$
Tập nghiệm của bất phương trình $({2^{{x^2} - 4}} - 1).\ln {x^2} < 0$ là:
Điều kiện: \(x \ne 0\).
\(\begin{array}{l}({2^{{x^2} - 4}} - 1) \ln{x^2} < 0 \Rightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}({2^{{x^2} - 4}} - 1) > 0\\ \ln{x^2} < 0\end{array} \right.\\\left\{ \begin{array}{l}({2^{{x^2} - 4}} - 1) < 0\\ \ln{x^2} > 0\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{2^{{x^2} - 4}} > 1\\{x^2} < 1\end{array} \right.\\\left\{ \begin{array}{l}{2^{{x^2} - 4}} < 1\\{x^2} > 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}{x^2} - 4 > 0\\{x^2} < 1\end{array} \right.\\\left\{ \begin{array}{l}{x^2} - 4 < 0\\{x^2} > 1\end{array} \right.\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}x > 2;x < - 2\\ - 1 < x < 1\end{array} \right.\\\left\{ \begin{array}{l} - 2 < x < 2\\x > 1;x < - 1\end{array} \right.\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 2 < x < - 1\\1 < x < 2\end{array} \right. \Rightarrow x \in \left( { - 2; - 1} \right) \cup \left( {1;2} \right)\end{array}\)
Tập hợp nghiệm của bất phương trình ${\log _{\frac{1}{3}}}\left( {{x^2} - 2x + 1} \right) < {\log _{\frac{1}{3}}}\left( {x - 1} \right)$ là:
Điều kiện: $\left\{ \begin{array}{l}{x^2} - 2x + 1 > 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{\left( {x - 1} \right)^2} > 0\\x - 1 > 0\end{array} \right. \Leftrightarrow x > 1$
${\log _{\dfrac{1}{3}}}({x^2} - 2x + 1) < {\log _{\dfrac{1}{3}}}(x - 1) \Leftrightarrow {x^2} - 2x + 1 > x - 1 > 0$
$ \Leftrightarrow \left\{ \begin{array}{l}{x^2} - 3x + 2 > 0\\x - 1 > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left( {x - 1} \right)(x - 2) > 0\\x - 1 > 0\end{array} \right. \Leftrightarrow x > 2$
Nghiệm của bất phương trình ${\log _2}(x + 1) + {\log _{\frac{1}{2}}}\sqrt {x + 1} \le 0$ là :
Điều kiện $x > -1$.
Khi đó ta có:
$\begin{array}{l}{\log _2}(x + 1) - lo{g_2}\sqrt {x + 1} \le 0 \Leftrightarrow {\log _2}\dfrac{{x + 1}}{{\sqrt {x + 1} }} \le 0 \Leftrightarrow \dfrac{{x + 1}}{{\sqrt {x + 1} }} \le 1\\ \Leftrightarrow \dfrac{{{{(\sqrt {x + 1} )}^2}}}{{\sqrt {x + 1} }} \le 1 \Leftrightarrow \sqrt {x + 1} \le 1 \Leftrightarrow x \le 0\end{array}$
Kết hợp với điều kiện ta được: $ - 1 < x \le 0$
Giải bất phương trình \({\log _{0,7}}\left( {{{\log }_6}\dfrac{{{x^2} + x}}{{x + 4}}} \right) < 0\)
${\log _{0,7}}({\log _6}\dfrac{{{x^2} + x}}{{x + 4}}) < 0$ .
Đkxđ: $\left\{ \begin{array}{l}{\log _6}\dfrac{{{x^2} + x}}{{x + 4}} > 0\\\dfrac{{{x^2} + x}}{{x + 4}} > 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l} - 4 < x < - 2\\x > 2\end{array} \right.(*)$
\(\begin{array}{l}{\log _6}\dfrac{{{x^2} + x}}{{x + 4}} > 0,{7^0} = 1 \Leftrightarrow \dfrac{{{x^2} + x}}{{x + 4}} > 6 \Leftrightarrow \dfrac{{{x^2} + x}}{{x + 4}} - 6 > 0\\ \Leftrightarrow \dfrac{{{x^2} - 5{\rm{x}} - 24}}{{x + 4}} > 0 \Leftrightarrow \dfrac{{(x - 8)(x + 3)}}{{x + 4}} > 0\end{array}\)
Xét dấu \(f\left( x \right) = \dfrac{{(x - 8)(x + 3)}}{{x + 4}}\):
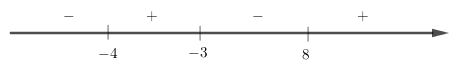
Vậy \( - 4 < x < - 3\) hoặc \(x > 8\).
Kết hợp với điều kiện ta được \( - 4 < x < - 3\) hoặc \(x > 8\).
Tìm tập hợp nghiệm $S$ của bất phương trình: \({\log _{\frac{\pi }{4}}}({x^2} + 1) < {\log _{\frac{\pi }{4}}}(2x + 4)\)
Điều kiện $x>-2$
Bất phương trình \( \Leftrightarrow {x^2} + 1 > 2x + 4\,(do\,\dfrac{\pi }{4} < 1)\) \( \Leftrightarrow {x^2} - 2x - 3 = (x + 1)(x - 3) > 0\)
Nên $x>3$ hoặc $x<-1$.
Kết hợp điều kiện $x>-2$ ta được $x>3$ hoặc $-2<x<-1$.
Giải bất phương trình \({\log _3}({2^x} - 3) < 0\)
Bất phương trình tương đương:
$\left\{ \begin{array}{l}{2^x} - 3 > 0\\{2^x} - 3 < 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x > {\log _2}3\\x < 2\end{array} \right. \Leftrightarrow {\log _2}3 < x < 2$.
Với \(m\) là tham số thực dương khác $1$. Hãy tìm tập nghiệm \(S\) của bất phương trình
\({\log _m}(2{x^2} + x + 3) \le {\log _m}(3{x^2} - x)\). Biết rằng \(x = 1\) là một nghiệm của bất phương trình.
Điều kiện: \(\left\{ \begin{array}{l}2{x^2} + x + 3 > 0\\3{x^2} - x > 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x > \dfrac{1}{3}\\x < 0\end{array} \right.\)
Do \(x=1\) là một nghiệm của bất phương trình nên \({\log _m}(2.{1^2} + 1 + 3) \le {\log _m}(3.{1^2} - 1) \Leftrightarrow {\log _m}6 \le {\log _m}2 \Leftrightarrow 0<m < 1\)
Khi đó, ta có:
\({\log _m}(2{x^2} + x + 3) \le {\log _m}(3{x^2} - x)\)
\(\Leftrightarrow 2{x^2} + x + 3 \ge 3{x^2} - x\)\( \Leftrightarrow {x^2} - 2x - 3 \le 0 \Leftrightarrow - 1 \le x \le 3\)
Kết hợp với điều kiện xác định ta có nghiệm của bpt là : \(S = \left[ { - 1;0} \right) \cup \left( {\dfrac{1}{3};3} \right)\)
Xác định tập nghiệm $S$ của bất phương trình $\ln{x^2} > \ln\left( {4x - 4} \right)$
Điều kiện $x>1$
$\ln{x^2} > \ln\left( {4x - 4} \right)$
\( \Leftrightarrow {x^2} > 4x - 4\, \Leftrightarrow {(x - 2)^2} > 0 \Leftrightarrow x \ne 2\)
\(S = \left( {1; + \infty } \right)\backslash \left\{ 2 \right\}\)
Tập nghiệm của bất phương trình $2017{\log _2}x \le {4^{{{\log }_2}9}}$ là
$2017{\log _2}x \le {9^{{{\log }_2}4}} = 81$
$ \Leftrightarrow {\log _2}x = \dfrac{{81}}{{2017}} = > 0 < x \le \sqrt[{2017}]{{{2^{81}}}}$
Tập nghiệm của phương trình \({\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1\) là
Điều kiện: $x>0$; ${\log _{\frac{1}{2}}}x > 0 \Rightarrow x < {\left( {\dfrac{1}{2}} \right)^0} = 1$
\({\log _3}\left( {{{\log }_{\frac{1}{2}}}x} \right) < 1 = {\log _3}3 \Leftrightarrow {\log _{\frac{1}{2}}}x < 3 = {\log _{\frac{1}{2}}}{\left( {\dfrac{1}{2}} \right)^3}\)
\( \Leftrightarrow x > {\left( {\dfrac{1}{2}} \right)^3} = \dfrac{1}{8}\) vì \(\dfrac{1}{2} < 1\)
Giải bất phương trình: $\log _2^2x - 4033{\log _2}x + 4066272 \le 0$ .
Điều kiện: $x>0$
Đặt $t = {\log _2}x$
BPT $ \Leftrightarrow {t^2} - 4033t + 4066272 \le 0$
$ \Leftrightarrow 2016 \le t \le 2017$
=>$2016 \le {\log _2}x \le 2017$
$ \Leftrightarrow {2^{2016}} \le x \le {2^{2017}}$
Tìm tập nghiệm $S$ của bất phương trình ${\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}(x) > {\log _2}({x^2} - x) - 1$
Thử giá trị $x = 3:{\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}\left( x \right) - {\log _2}\left( {{x^2} - x} \right) + 1 < 0$: Loại đáp án A
Thử giá trị $x = 2:{\log _{\frac{1}{2}}}\left( {x + 2} \right) - {\log _{\frac{1}{{\sqrt 2 }}}}\left( x \right) - {\log _2}\left( {{x^2} - x} \right) + 1 = 0$: Loại đáp án D
Thử giá trị $x = 0,5$: MATH ERROR: Loại đáp án C
Tập nghiệm của bất phương trình ${\log _3}x \le {\log _{\frac{1}{3}}}(2x)$ là nửa khoảng $(a;b{\rm{]}}$. Giá trị của ${a^2} + {b^2}$ bằng
Điều kiện: \(x > 0\).
${\log _3}x \le {\log _{\frac{1}{3}}}(2x) \Leftrightarrow {\log _3}x \le - {\log _3}(2x)$
$ \Leftrightarrow {\log _3}x + {\log _3}(2x) \le 0$
$ \Leftrightarrow {\log _3}(2{x^2}) \le 0$
$ \Leftrightarrow 2{x^2} \le 1$
$ \Leftrightarrow - \dfrac{{\sqrt 2 }}{2} \le x \le \dfrac{{\sqrt 2 }}{2}$.
Kết hợp với \(x > 0\) ta được \(0 < x \le \dfrac{{\sqrt 2 }}{2}\).
Do đó $\left\{ \begin{array}{l}a = 0\\b = \dfrac{{\sqrt 2 }}{2}\end{array} \right. \Rightarrow {a^2} + {b^2} = \dfrac{1}{2}$

