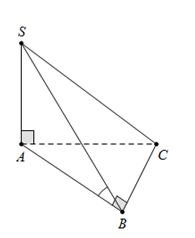
Cho hình chóp $S.ABC$ có đáy \(ABC\). là tam giác vuông tại $B,$ $BC = a$. Cạnh bên $SA = a$ vuông góc với mặt phẳng đáy. Góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$ bằng ${45^0}$. Độ dài $AC$ bằng
Ta có $\left( {SBC} \right) \cap \left( {ABC} \right) = BC \Rightarrow BC$ là giao tuyến.
Mặt khác $SA \bot \left( {ABC} \right)$ và $\Delta ABC$ vuông tại $B \Rightarrow AB \bot BC$.
Nên $\left\{ \begin{array}{l}SA \bot BC\\AB \bot BC\end{array} \right. \Rightarrow $$BC \bot \left( {SAB} \right) \Rightarrow BC \bot SB$
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SB \bot BC\\\left( {ABC} \right) \supset AB \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SB;AB} \right)} = \widehat {SBA} = {45^0}$
Xét $\Delta SAB$ vuông tại $A$, có $\widehat {SBA} = {45^0} \Rightarrow SA = AB = a$.
Mà $A{C^2} = A{B^2} + B{C^2} = 2{a^2} \Rightarrow AC = a\sqrt 2 $.
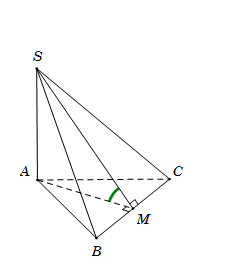
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác đều cạnh $a$. Cạnh bên $SA = a\sqrt 3 $ và vuông góc với mặt đáy $\left( {ABC} \right)$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABC} \right)$. Mệnh đề nào sau đây đúng?
Gọi \(M\) là trung điểm của $BC$, suy ra $AM \bot BC$
Ta có $\left\{ \begin{array}{l}AM \bot BC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM$
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SM \bot BC\\\left( {ABC} \right) \supset AM \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SM;AM} \right)} = \widehat {SMA}.$
Tam giác $ABC$ đều cạnh $a$, suy ra trung tuyến $AM = \dfrac{{a\sqrt 3 }}{2}.$
Tam giác vuông $SAM$, có $\sin \widehat {SMA} = \dfrac{{SA}}{{SM}} = \dfrac{{SA}}{{\sqrt {S{A^2} + A{M^2}} }} = \dfrac{{2\sqrt 5 }}{5}.$
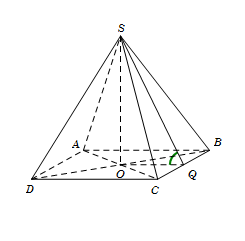
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông tâm $O$, cạnh $a$. Đường thẳng $SO$ vuông góc với mặt phẳng đáy $\left( {ABCD} \right)$ và $SO = \dfrac{{a\sqrt 3 }}{2}$. Tính góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$.
Gọi \(Q\) là trung điểm \(BC\), suy ra \(OQ \bot BC\).
Ta có $\left\{ \begin{array}{l}BC \bot OQ\\BC \bot SO\end{array} \right. \Rightarrow BC \bot \left( {SOQ} \right) \Rightarrow BC \bot SQ.$
Do đó
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SQ \bot BC\\\left( {ABCD} \right) \supset OQ \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SQ;OQ} \right)} = \widehat {SQO}.$
Tam giác vuông $SOQ$, có $\tan \widehat {SQO} = \dfrac{{SO}}{{OQ}} = \sqrt 3 \Rightarrow \widehat {SQO} = {60^0}$
Vậy mặt phẳng $\left( {SBC} \right)$ hợp với mặt đáy $\left( {ABCD} \right)$ một góc ${60^0}.$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi cạnh $a$, các cạnh $SA = SB = a,$ $SD = a\sqrt 2 $. Góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right)$ bằng ${90^0}.$ Độ dài đoạn thẳng $BD$
Gọi $I$ là tâm của hình thoi $ABCD$.
Và $H$ là hình chiếu vuông góc của $S$ lên $BD$.
$\widehat {\left( {\left( {SBD} \right);\left( {ABCD} \right)} \right)} = {90^0} \Rightarrow \left( {SBD} \right) \bot \left( {ABCD} \right) \Rightarrow SH \bot \left( {ABCD} \right)$.
Khi đó $\left\{ \begin{array}{l}SH \bot AC\\BD \bot AC\end{array} \right. \Rightarrow AC \bot \left( {SBD} \right) \Rightarrow AC \bot SI$.
Mà $I$ là trung điểm của \(AC \Rightarrow \Delta SAC\) cân tại S \( \Rightarrow SA = SB = SC=BC=a\).
\(\Delta SAC = \Delta BAC\left( {c.c.c} \right) \Rightarrow BI = SI = \dfrac{1}{2}BD \Rightarrow \Delta SBD\) vuông tại S
$ \Rightarrow B{D^2} = S{B^2} + S{D^2} = {a^2} + {\left( {a\sqrt 2 } \right)^2} = 3{a^2} \Rightarrow BD = a\sqrt 3 $.

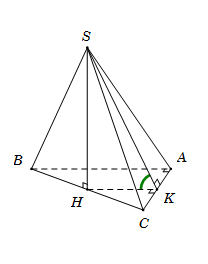
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $\widehat {ABC} = {60^0}$, tam giác $SBC$ là tam giác đều có bằng cạnh $2a$ và nằm trong mặt phẳng vuông với đáy. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {ABC} \right)$. Mệnh đề nào sau đây đúng?
Gọi $H$ là trung điểm của \(BC\), suy ra $SH \bot BC \Rightarrow SH \bot \left( {ABC} \right)$.
Gọi $K$ là trung điểm $AC$, suy ra $HK$//$AB$ nên $HK \bot AC$.
Ta có $\left\{ \begin{array}{l}AC \bot HK\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHK} \right) \Rightarrow AC \bot SK.$
$\left\{ \begin{array}{l}\left( {SAC} \right) \cap \left( {ABC} \right) = AC\\\left( {SAC} \right) \supset SK \bot AC\\\left( {ABC} \right) \supset HK \bot AC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SAC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SK;HK} \right)} = \widehat {SKH}.$
Tam giác vuông $ABC$, có $AB = BC.\cos \widehat {ABC} = a \Rightarrow HK = \dfrac{1}{2}AB = \dfrac{a}{2}.$
Tam giác \(SBC\) đều cạnh \(2a\) có đường cao \(SH = \dfrac{{2a\sqrt 3 }}{2}\)
Tam giác vuông $SHK$, có $\tan \widehat {SKH} = \dfrac{{SH}}{{HK}} = \dfrac{{\dfrac{{2a\sqrt 3 }}{2}}}{{\dfrac{a}{2}}} = 2\sqrt 3 $.
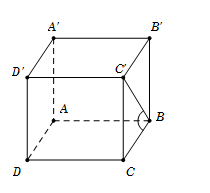
Cho hình lăng trụ tứ giác đều $ABCD.A'B'C'D'$ có đáy cạnh bằng $a,$ góc giữa hai mặt phẳng $\left( {ABCD} \right)$ và $\left( {ABC'} \right)$ có số đo bằng ${60^0}.$ Độ dài cạnh bên của hình lăng trụ bằng
Vì $ABCD.A'B'C'D'$ là lăng trụ tứ giác đều
$ \Rightarrow \left\{ \begin{array}{l}AB \bot BB'\\AB \bot BC\end{array} \right. \Rightarrow AB \bot \left( {BB'C'B} \right) \Rightarrow AB \bot BC'$
$\left\{ \begin{array}{l}\left( {ABC'} \right) \cap \left( {ABCD} \right) = AB\\\left( {ABC'} \right) \supset BC' \bot AB\\\left( {ABCD} \right) \supset BC \bot AB\end{array} \right. \Rightarrow \widehat {\left( {\left( {ABC'} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {BC';BC} \right)} = \widehat {C'BC} = {60^0}.$
Tam giác $BCC'$ vuông tại $C,$ có $\tan \widehat {C'BC} = \dfrac{{CC'}}{{BC}} \Rightarrow CC' = \tan {60^0}.a = a\sqrt 3 .$
Cho hình chóp đều $S.ABCD$ có tất cả các cạnh bằng $a$. Gọi $M$ là trung điểm $SC$. Tính góc $\varphi $ giữa hai mặt phẳng $\left( {MBD} \right)$ và $\left( {ABCD} \right)$.
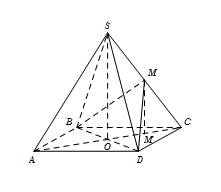
Gọi M’ là trung điểm $OC \Rightarrow MM'\parallel SO \Rightarrow MM' \bot \left( {ABCD} \right).$
Theo công thức diện tích hình chiếu, ta có ${S_{\Delta \,M'BD}} = \cos \varphi .{S_{\Delta \,MBD}}$
$\begin{array}{l} \Rightarrow \cos \varphi = \dfrac{{{S_{\Delta \,M'BD}}}}{{{S_{\Delta \,MBD}}}} = \dfrac{{BD.M'O}}{{BD.MO}} = \dfrac{{M'O}}{{MO}} = \dfrac{{\dfrac{1}{2}OC}}{{\dfrac{1}{2}SA}}\\ = \dfrac{{\sqrt {B{C^2} - O{B^2}} }}{{SA}} = \dfrac{{\sqrt {{a^2} - {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2}} }}{a} = \dfrac{{\sqrt 2 }}{2} \Rightarrow \varphi = {45^0}.\end{array}$
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình thoi tâm $I$, cạnh $a$, góc $\widehat {BAD} = {60^0}$, $SA = SB = SD = \dfrac{{a\sqrt 3 }}{2}$. Gọi \(\varphi \) là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {ABCD} \right).$ Mệnh đề nào sau đây đúng?
Từ giả thiết suy ra tam giác $ABD$ đều cạnh $a$.
Gọi $H$ là hình chiếu của $S$ trên mặt phẳng $\left( {ABCD} \right)$.
Do $SA = SB = SD$ nên suy ra $H$ là tâm của tam gác đều $ABD$.
Suy ra $AH = \dfrac{2}{3}AI = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3},HI = \dfrac{1}{3}AI = \dfrac{1}{3}\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{6}$
và $SH = \sqrt {S{A^2} - A{H^2}} = \dfrac{{a\sqrt {15} }}{6}.$
Vì $ABCD$ là hình thoi nên $HI \bot BD$. Tam giác $SBD$ cân tại $S$ nên $SI \bot BD$. Do đó $\widehat {\left( {SBD} \right);\left( {ABCD} \right)} = \widehat {\left( {SI;AI} \right)} = \widehat {SIH}.$.
Trong tam vuông $SHI$, có $\tan \widehat {SIH} = \dfrac{{SH}}{{HI}} = \sqrt 5 .$

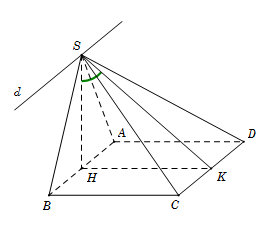
Trong không gian cho tam giác đều $SAB$ và hình vuông $ABCD$ cạnh $a$ nằm trên hai mặt phẳng vuông góc. Gọi $H,$ $K$ lần lượt là trung điểm của $AB$, $CD$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$. Mệnh đề nào sau đây đúng?
Dễ dàng xác định giao tuyến của hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SCD} \right)$ là đường thẳng $d$ đi qua $S$ và song song với AB và CD.
Trong mặt phẳng $\left( {SAB} \right)$ có $SH \bot AB \Rightarrow SH \bot d.$
Ta có $\left\{ \begin{array}{l}CD \bot HK\\CD \bot SH\end{array} \right. \Rightarrow CD \bot \left( {SHK} \right) \Rightarrow CD \bot SK \Rightarrow d \bot SK.$
Từ đó suy ra
$\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SCD} \right) = d\\\left( {SAB} \right) \supset SH \bot d\\\left( {SCD} \right) \supset SK \bot d\end{array} \right. \Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {SH;SK} \right)} = \widehat {HSK}.$
Trong tam giác vuông $SHK$, có $\tan \widehat {HSK} = \dfrac{{HK}}{{SH}} = \dfrac{a}{{\dfrac{{a\sqrt 3 }}{2}}} = \dfrac{{2\sqrt 3 }}{3}.$
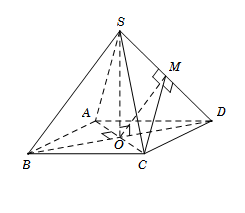
Cho hình chóp đều $S.ABCD$ có tất cả các cạnh đều bằng $a$. Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBD} \right)$ và $\left( {SCD} \right)$. Mệnh đề nào sau đây đúng?
Gọi $O = AC \cap BD$. Do hình chóp $S.ABCD$ đều nên $SO \bot \left( {ABCD} \right)$.
Gọi $M$ là trung điểm của $SD.$ Tam giác $SCD$ đều nên $CM \bot SD$.
Tam giác $SBD$ có $SB = SD = a,$ $BD = a\sqrt 2 $
Suy ra $\Delta \,SBD$ vuông tại $S \Rightarrow SB \bot SD \Rightarrow OM \bot SD.$
Do đó
$\left\{ \begin{array}{l}\left( {SBD} \right) \cap \left( {SCD} \right) = SD\\\left( {SBD} \right) \supset OM \bot SD\\\left( {SCD} \right) \supset CM \bot SD\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBD} \right);\left( {SCD} \right)} \right)} = \widehat {\left( {OM;CM} \right)} = \widehat {OMC}.$
Ta có $\left\{ \begin{array}{l}OC \bot BD\\OC \bot SO\end{array} \right. \Rightarrow OC \bot \left( {SBD} \right) \Rightarrow OC \bot OM$.
Tam giác vuông MOC vuông tại O, có $\tan \widehat {CMO} = \dfrac{{OC}}{{OM}} = \dfrac{{\dfrac{1}{2}a\sqrt 2 }}{{\dfrac{1}{2}a}} = \sqrt 2 $.
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $B,$ cạnh bên $SA$ vuông góc với đáy. Gọi $E,\,\,\,F$ lần lượt là trung điểm của cạnh $AB$ và $AC.$ Góc giữa hai mặt phẳng $\left( {SEF} \right)$ và $\left( {SBC} \right)$ là
Gọi $\left( d \right)$ là đường thẳng đi qua $S$ và song song với EF.
Vì EF là đường trung bình tam giác ABC suy ra EF // BC.
Khi đó d // EF // BC$ \Rightarrow \left( {SEF} \right) \cap \left( {SBC} \right) = \left( d \right)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right).$
Ta có $\left\{ \begin{array}{l}SA \bot BC\,\,\,\,\left( {SA \bot \left( {ABC} \right)} \right)\\AB \bot BC\end{array} \right.$$ \Rightarrow $$BC \bot \left( {SAB} \right) \Rightarrow \left\{ \begin{array}{l}BC \bot SE\\BC \bot SB\end{array} \right.\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right).$
Từ $\left( 1 \right),\,\,\left( 2 \right)$ suy ra $\left\{ \begin{array}{l}\left( d \right) \bot SE\\\left( d \right) \bot SB\end{array} \right. \Rightarrow \widehat {\left( {\left( {SEF} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {SE;SB} \right)} = \widehat {BSE}.$

Cho hình chóp đều $S.ABC$ có cạnh đáy bằng $a,$ góc giữa mặt bên và mặt đáy bằng ${60^0}.$ Tính độ dài đường cao $SH$ của khối chóp.
Gọi $H$ là chân đường cao kẻ từ đỉnh $S$ xuống mặt phẳng (ABC).
Vì S.ABC là hình chóp đều có SA = SB = SC nên suy ra H chính là tâm đường tròn ngoại tiếp tam giác ABC.
Gọi M là trung điểm của BC, ta có
$\left\{ \begin{array}{l}BC \bot AM\\BC \bot SH\end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \bot SM$.
Khi đó
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SM \bot BC\\\left( {ABC} \right) \supset AM \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {SM;AM} \right)} = \widehat {SMA} = {60^0}$.
Tam giác ABC đều cạnh a có $AM = \dfrac{{a\sqrt 3 }}{2} \Rightarrow HM = \dfrac{{AM}}{3} = \dfrac{{a\sqrt 3 }}{6}.$
Tam giác AHM vuông tại H, có $SH = \tan {60^0}.\dfrac{{a\sqrt 3 }}{6} = \dfrac{a}{2}.$
Vậy độ dài đường cao $SH = \dfrac{a}{2}.$
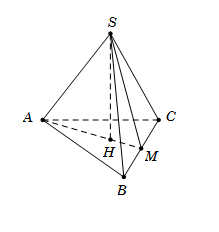
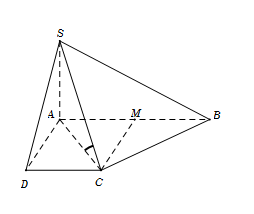
Cho hình chóp $S.ABCD$ có đáy là hình thang vuông $ABCD$ vuông tại $A$ và $D$, $AB = 2a,$ $AD = CD = a$. Cạnh bên $SA = a$ và vuông góc với mặt phẳng $\left( {ABCD} \right).$ Gọi $\varphi $ là góc giữa hai mặt phẳng $\left( {SBC} \right)$ và $\left( {ABCD} \right)$ . Mệnh đề nào sau đây đúng?
Gọi $M$ là trung điểm $AB$ $\, \Rightarrow ADCM$ là hình vuông.
Vì$\,CM = AD = a = \dfrac{{AB}}{2}$. Suy ra tam giác $ACB$ có trung tuyến bằng nửa cạnh đáy nên vuông tại $C$.
Ta có $\left\{ \begin{array}{l}BC \bot SA\\BC \bot AC\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot SC.$
Do đó :
$\left\{ \begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\\\left( {SBC} \right) \supset SC \bot BC\\\left( {ABCD} \right) \supset AC \bot BC\end{array} \right. \Rightarrow \widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA}.$
Tam giác $SAC$ vuông tại $A$$ \Rightarrow \tan \varphi = \dfrac{{SA}}{{AC}} = \dfrac{{SA}}{{\sqrt {A{D^2} + C{D^2}} }} = \dfrac{a}{{a\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}.$
Cho hình lăng trụ đứng $ABC.A'B'C'$, đáy $ABC$ là tam giác đều $a$. Gọi $I$ là trung điểm của $BC$. Góc giữa hai mặt phẳng $\left( {C'AI} \right)$ và $\left( {ABC} \right)$ bằng ${60^0}$. Độ dài $AA'$ bằng
Ta có $I$ là trung điểm của $BC\,\, \Rightarrow AI \bot BC$
$ABC.A'B'C'$ là lăng trụ đứng $ \Rightarrow C'C \bot \left( {ABC} \right).$
$ \Rightarrow C'C \bot AI$ mà $AI \bot BC \Rightarrow AI \bot \left( {BCC'B'} \right) \Rightarrow AI \bot C'I$
Suy ra
$\left\{ \begin{array}{l}\left( {C'AI} \right) \cap \left( {ABC} \right) = AI\\\left( {C'AI} \right) \supset C'I \bot AI\\\left( {ABC} \right) \supset BC \bot AI\end{array} \right. \Rightarrow \widehat {\left( {\left( {C'AI} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {C'I;BC} \right)} = \widehat {C'IC} = {60^0}$
Xét $\Delta \,C'CI$ vuông tại $C$, có : $\tan \widehat {C'IC} = \dfrac{{CC'}}{{IC}} \Rightarrow CC' = \tan {60^0}.\dfrac{a}{2} = \dfrac{{a\sqrt 3 }}{2} \Rightarrow AA' = \dfrac{{a\sqrt 3 }}{2}$

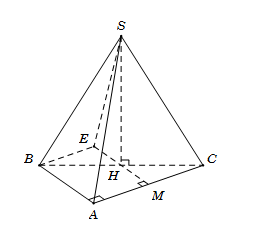
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông tại $A$, $AB = AC = a$. Hình chiếu vuông góc $H$ của $S$ trên mặt đáy $\left( {ABC} \right)$ trùng với tâm đường tròn ngoại tiếp tam giác $ABC$ và $SH = \dfrac{{a\sqrt 6 }}{2}$. Gọi $\varphi $ là góc giữa hai đường thẳng $SB$ và $AC$. Mệnh đề nào sau đây đúng?
Gọi $H$ là trung điểm $BC.$ Tam giác $ABC $ vuông tại $A$ nên $H$ trung điểm của $BC.$
Theo giả thiết, ta có $SH \bot \left( {ABC} \right)$
Qua $B$ kẻ $Bx$//$AC$. Khi đó $\widehat {\left( {SB;AC} \right)} = \widehat {\left( {SB;Bx} \right)}$
Kẻ $HE \bot Bx$ tại $E$, cắt $AC$ tại $M$
Suy ra AMEB là hình chữ nhật nên $\left\{ \begin{array}{l}BE = AM = \dfrac{1}{2}AC = \dfrac{a}{2}\\HE = HM = \dfrac{1}{2}AB = \dfrac{a}{2}\end{array} \right.$
Ta có $\left\{ \begin{array}{l}Bx \bot HE\\Bx \bot SH\end{array} \right. \Rightarrow Bx \bot \left( {SHE} \right) \Rightarrow Bx \bot SE$
Tam giác vuông $SEB$ vuông tại $E,$ có $\cot \widehat {SBE} = \dfrac{{BE}}{{SE}} = \dfrac{{AM}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\dfrac{a}{2}}}{{\sqrt {\dfrac{{6{a^2}}}{4} + \dfrac{{{a^2}}}{4}} }} = \dfrac{{\sqrt 7 }}{7}$
Trong mặt phẳng $\left( P \right)$ cho nửa đường tròn đường kính $AB = 2R$ và điểm $C$ thuộc nửa đường tròn đó sao cho $AC = R$. Trên đường thẳng vuông góc với $\left( P \right)$ tại $A$ lấy điểm $S$ sao cho góc giữa hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SBC} \right)$ bằng ${60^0}$. Gọi $H,\,\,K$ lần lượt là hình chiếu của $A$ lên $SB,\,\,SC$. Độ dài cạnh $SA$ tính theo $R$ là
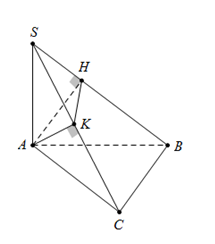
Ta có $\left\{ \begin{array}{l}BC \bot AC\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAC} \right) \Rightarrow BC \bot AK$.
Do đó $AK \bot \left( {SBC} \right) \Rightarrow AK \bot KH$.
\(\begin{array}{l}\left\{ \begin{array}{l}AH \bot SB\\AK \bot SB\end{array} \right. \Rightarrow SB \bot \left( {AHK} \right) \Rightarrow SB \bot HK\\\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {SBC} \right) = SB\\\left( {SAB} \right) \supset AH \bot SB\\\left( {SAC} \right) \supset HK \bot SB\end{array} \right.\Rightarrow \widehat {\left( {\left( {SAB} \right);\left( {SBC} \right)} \right)} = \widehat {\left( {AH;HK} \right)} = \widehat {AHK} = {60^0}\end{array}\)
Xét tam giác AHK vuông tại K có:
$AK = AH.\sin {60^0} \Leftrightarrow A{K^2} = \dfrac{3}{4}A{H^2} \Leftrightarrow \dfrac{3}{4}\dfrac{1}{{A{K^2}}} = \dfrac{1}{{A{H^2}}}$.
Đặt SA = a, áp dụng hệ thức lượng, ta được
- $\dfrac{1}{{A{K^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{C^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{R^2}}}$
- $\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{B^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{R^2}}}$
Suy ra $\dfrac{3}{4}\left( {\dfrac{1}{{{a^2}}} + \dfrac{1}{{{R^2}}}} \right) = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{R^2}}} \Leftrightarrow \dfrac{1}{4}\dfrac{1}{{{a^2}}} = \dfrac{1}{2}\dfrac{1}{{{R^2}}} \Leftrightarrow {a^2} = \dfrac{{{R^2}}}{2} \Leftrightarrow a = \dfrac{R}{{\sqrt 2 }}$.
Trong mặt phẳng $\left( P \right)$ cho tam giác đều $ABC$ cạnh $a$. Trên các đường thẳng vuông góc với mặt phẳng $\left( P \right)$ tại $B$ và $C$ lấy điểm $D,\,\,E$ cùng phía so với $\left( P \right)$ sao cho $BD = \dfrac{{a\sqrt 3 }}{2}$ và $CE = a\sqrt 3 $. Tính góc giữa hai mặt phẳng $\left( {ADE} \right)$ và $\left( {ABC} \right)$.
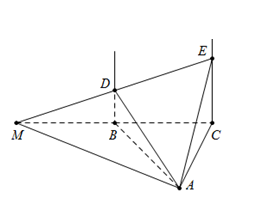
Vẽ $BC \cap DE = M$$ \Rightarrow \left( {ADE} \right) \cap \left( {ABC} \right) = AM$.
Ta có $BD$//$CE \Rightarrow \dfrac{{BD}}{{CE}} = \dfrac{{MB}}{{MC}} = \dfrac{1}{2} $$\Rightarrow BM = BC = BA$.
Suy ra $\Delta AMC$ vuông tại $A$ $ \Rightarrow AM \bot AC$.
$ \Rightarrow \left\{ \begin{array}{l}AM \bot AC\\AM \bot EC\end{array} \right. \Rightarrow AM \bot \left( {ACE} \right) \Rightarrow AM \bot AE \Rightarrow \Delta AME$ vuông tại $A$.
Mặt khác ta có: $\left\{ \begin{array}{l}\left( {ADE} \right) \cap \left( {ABC} \right) = AM\\\left( {ADE} \right) \supset AE \bot AM\\\left( {ABC} \right) \supset AC \bot AM\end{array} \right. $$\Rightarrow \widehat {\left( {\left( {ADE} \right);\left( {ABC} \right)} \right)} = \widehat {\left( {AE;AC} \right)} = \widehat {EAC}$.
Xét $\Delta AEC$ vuông tại C, có $\tan \widehat {EAC} = \dfrac{{EC}}{{AC}} = \dfrac{{a\sqrt 3 }}{a} = \sqrt 3 $$ \Rightarrow \widehat {EAC} = {60^0}$.
Cho hai tam giác $ACD$ và $BCD$ nằm trên hai mặt phẳng vuông góc với nhau và $AC = AD = BC = BD = a,\,\,\,CD = 2x.$ Với giá trị nào của $x$ thì hai mặt phẳng $\left( {ABC} \right)$ và $\left( {ABD} \right)$ vuông góc.
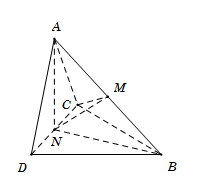
Gọi $M, N$ lần lượt là trung điểm của $AB, CD.$
Ta có $AN \bot CD$ mà $\left( {ACD} \right) \bot \left( {BCD} \right)$
$ \Rightarrow AN \bot \left( {BCD} \right) \Rightarrow AN \bot BN \Rightarrow \Delta ANB$ vuông tại N \( \Rightarrow NM = \dfrac{{AB}}{2}\,\,\left( 1 \right)\)
Tam giác $ABC$ cân tại $C,$ có $M$ là trung điểm của $AB$ $ \Rightarrow CM \bot AB.$
Giả sử $\left( {ABC} \right) \bot \left( {ABD} \right)$ mà $CM \bot AB$$ \Rightarrow CM \bot \left( {ABD} \right) \Rightarrow CM \bot DM.$
Khi đó, $\Delta \,MCD$ vuông tại $M$. Ta có \(\Delta ABC = \Delta ABD\,\,\left( {c.c.c} \right) \Rightarrow CM = DM \Rightarrow \Delta MCD\) vuông cân tại M.
$ \Rightarrow \,\,MN = \dfrac{{CD}}{2}\,\,\,\left( 2 \right)$.
Từ (1) và (2) $ \Rightarrow AB = CD = 2x$
Lại có $\Delta ACD = \Delta BCD\,\,\left( {c.c.c} \right) \Rightarrow AN = BN = \sqrt {A{C^2} - C{N^2}} = \sqrt {{a^2} - {x^2}} ,$ mà $A{B^2} = A{N^2} + B{N^2}.$
Suy ra $2\left( {{a^2} - {x^2}} \right) = 4{x^2} \Leftrightarrow {a^2} = 3{x^2} \Leftrightarrow x = \dfrac{{a\sqrt 3 }}{3}.$
Cho hình chóp $S.ABC$ có đáy $ABC$ là tam giác vuông cân tại $C$. Gọi $H$ là trung điểm $AB$. Biết rằng $SH$ vuông góc với mặt phẳng $\left( {ABC} \right)$ và $AB = SH = a.$ Tính cosin của góc $\alpha $ tọa bởi hai mặt phẳng $\left( {SAB} \right)$ và $\left( {SAC} \right)$.
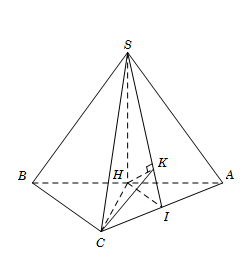
Ta có $SH \bot \left( {ABC} \right) \Rightarrow SH \bot CH$ (1)
Tam giác ABC cân tại C nên $CH \bot AB$ (2)
Từ (1) và (2), suy ra $CH \bot \left( {SAB} \right)$
Gọi I là trung điểm $AC$ $\Rightarrow \,\,HI//BC\xrightarrow{BC\,\bot \,\,AC}HI\bot AC$ (3)
Mặt khác $AC \bot SH$ (do $SH \bot \left( {ABC} \right)$) (4)
Từ (3) và (4), suy ra $AC \bot \left( {SHI} \right)$
Kẻ $HK \bot SI{\rm{ }}\,\left( {K \in SI} \right)$ (5)
Từ $AC \bot \left( {SHI} \right) \Rightarrow AC \bot HK$ (6)
Từ (5) và (6), suy ra $HK \bot \left( {SAC} \right)$
Vì $\left\{ \begin{array}{l}HK \bot \left( {SAC} \right)\\HC \bot \left( {SAB} \right)\end{array} \right.$ nên góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SAB} \right)$ bằng góc giữa hai đường thẳng $HK$ và $HC$
Ta có \(HK \bot \left( {SAC} \right) \Rightarrow HK \bot CK \Rightarrow \Delta CHK\) vuông tại $K.$
Do đó góc giữa hai mặt phẳng $\left( {SAC} \right)$ và $\left( {SAB} \right)$ là \(\widehat {CHK}\)
Có $CH = \dfrac{1}{2}AB = \dfrac{a}{2}$; $\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{I^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{{\left( {\dfrac{1}{2}.\dfrac{a}{{\sqrt 2 }}} \right)}^2}}} \Rightarrow HK = \dfrac{a}{3}$
Do đó $\cos \widehat {CHK} = \dfrac{{HK}}{{CH}} = \dfrac{{\dfrac{a}{3}}}{{\dfrac{a}{2}}} = \dfrac{2}{3}.$
Cho hình chóp S . ABCD có đáy là hình chữ nhật, biết \(AB = 2a,AD\). \(a,SA = 3a\) và SA vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \({CD}\) điểm \(E \in SA\) sao cho \(SE = a,{\mathop{\rm cosin}\nolimits} \) của góc giữa hai mặt phẳng \((SAC)\) và \(\left( {B{ME}} \right)\) bằng
\(\dfrac{1}{{\sqrt {15} }}\).
\(\dfrac{1}{{\sqrt {15} }}\).
\(\dfrac{1}{{\sqrt {15} }}\).
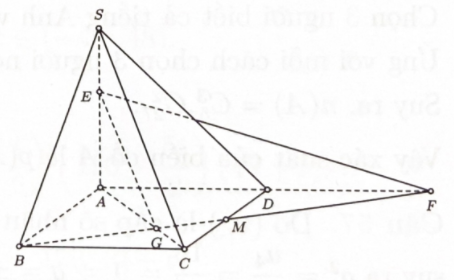
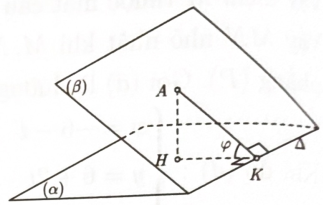
Bước 1: Gọi góc giữa hai mặt phẳng \((\alpha )\) và \((\beta )\) là góc \(\varphi \). \(G\) là trọng tâm \(\Delta BCD\), kéo dài tia BM cắt AD tại \(F\). Chứng minh \(\sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}}\)
Gọi góc giữa hai mặt phẳng \((\alpha )\) và \((\beta )\) là góc \(\varphi \). Khi đó \(\sin \varphi = \dfrac{{d(A,\alpha )}}{{d(A,\Delta )}}.\)
Gọi điểm \(G\) là trọng tâm \(\Delta BCD\), kéo dài tia BM cắt AD tại \(F\).
Ta có \((SAC) \cap (BEF) = EG\).
=> Góc giữa hai mặt phẳng \((SAC)\) và \((BME)\) là góc \(\varphi \) có \(\sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}}\).
Bước 2: Tính \(\sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}}\)
Ta có \(d(A,(BEF)) = \dfrac{{2a\sqrt 3 }}{3}\),
\(d(A,EG) = \dfrac{{AE \cdot AG}}{{\sqrt {A{E^2} + A{G^2}} }} = \dfrac{{a\sqrt {70} }}{7}\)
\( \Rightarrow \sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}} = \dfrac{{\sqrt {14} }}{{\sqrt {15} }}\)
\( \Rightarrow \cos \varphi = \dfrac{1}{{\sqrt {15} }}\)

