Cho hình chóp S . ABCD có đáy là hình chữ nhật, biết \(AB = 2a,AD\). \(a,SA = 3a\) và SA vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \({CD}\) điểm \(E \in SA\) sao cho \(SE = a,{\mathop{\rm cosin}\nolimits} \) của góc giữa hai mặt phẳng \((SAC)\) và \(\left( {B{ME}} \right)\) bằng
Trả lời bởi giáo viên
\(\dfrac{1}{{\sqrt {15} }}\).
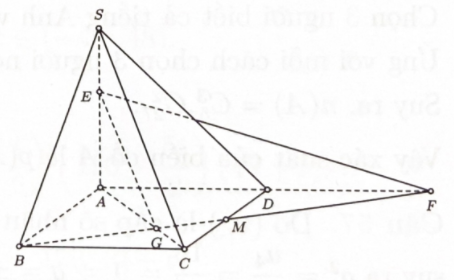
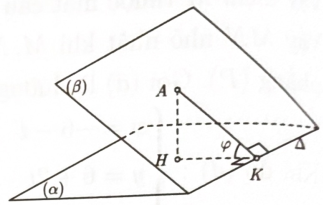
Bước 1: Gọi góc giữa hai mặt phẳng \((\alpha )\) và \((\beta )\) là góc \(\varphi \). \(G\) là trọng tâm \(\Delta BCD\), kéo dài tia BM cắt AD tại \(F\). Chứng minh \(\sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}}\)
Gọi góc giữa hai mặt phẳng \((\alpha )\) và \((\beta )\) là góc \(\varphi \). Khi đó \(\sin \varphi = \dfrac{{d(A,\alpha )}}{{d(A,\Delta )}}.\)
Gọi điểm \(G\) là trọng tâm \(\Delta BCD\), kéo dài tia BM cắt AD tại \(F\).
Ta có \((SAC) \cap (BEF) = EG\).
=> Góc giữa hai mặt phẳng \((SAC)\) và \((BME)\) là góc \(\varphi \) có \(\sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}}\).
Bước 2: Tính \(\sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}}\)
Ta có \(d(A,(BEF)) = \dfrac{{2a\sqrt 3 }}{3}\),
\(d(A,EG) = \dfrac{{AE \cdot AG}}{{\sqrt {A{E^2} + A{G^2}} }} = \dfrac{{a\sqrt {70} }}{7}\)
\( \Rightarrow \sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}} = \dfrac{{\sqrt {14} }}{{\sqrt {15} }}\)
\( \Rightarrow \cos \varphi = \dfrac{1}{{\sqrt {15} }}\)
Hướng dẫn giải:
Bước 1: Gọi góc giữa hai mặt phẳng \((\alpha )\) và \((\beta )\) là góc \(\varphi \). \(G\) là trọng tâm \(\Delta BCD\), kéo dài tia BM cắt AD tại \(F\). Chứng minh \(\sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}}\)
Bước 2: Tính \(\sin \varphi = \dfrac{{d(A,(BEF))}}{{d(A,EG)}}\)

