Một số bài toán về khảo sát hàm bậc ba, bậc bốn trùng phương
Kỳ thi ĐGTD ĐH Bách Khoa
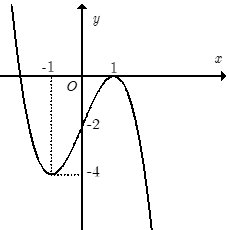
Đường cong trong hình vẽ bên là đồ thị của hàm số nào?
Nhận xét: Đường cong trong hình vẽ là đồ thị của hàm số bậc 3 có hệ số $a > 0$ nên loại đáp án A, C
Xét 2 đáp án B và D
Thay $x = 0;\,y = 2$ thì cả 2 đáp án B, D đều thỏa mãn
Thay $x = 2;\,y = - 2$ chỉ có đáp án B thỏa mãn
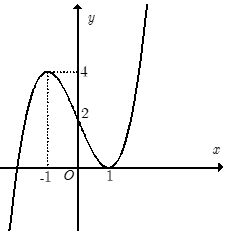
Hàm số nào sau đây có đồ thị như hình vẽ?
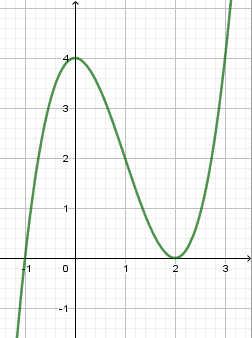
Đồ thị hàm số đi qua điểm $\left( {0;4} \right)$ nên loại A và D
Đồ thị hàm số cắt $Ox$ tại điểm $\left( { - 1;0} \right)$ và tiếp xúc $Ox$ tại $\left( {2;0} \right)$ nên phương trình hoành độ giao điểm $y = 0$ có 1 nghiệm đơn $x=-1$ và 1 nghiệm kép ${x_{2,3}} = 2$
Vậy chỉ có đáp án B thỏa mãn.
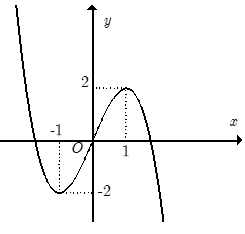
Hàm số nào sau đây có đồ thị như hình vẽ?
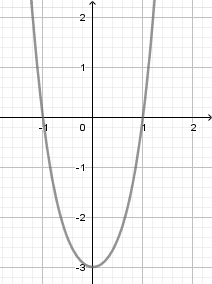
Từ dáng đồ thị ta có $a > 0$ nên loại A, C
Đồ thị hàm số có điểm cực tiểu là $\left( {0; - 3} \right).$
Do hàm số chỉ có một điểm cực trị nên $y' = 0$ phải có duy nhất một nghiệm ${x_0}$ và $y\left( {{x_0}} \right) = - 3.$
Kiểm tra ta chỉ thấy đáp án D là phù hợp.
Ngoài ra, đáp án B bị loại vì phương trình $y'=0$ ở đáp án B có $3$ nghiệm phân biệt.
Đồ thị sau đây là của hàm số nào?
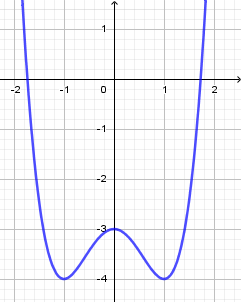
Từ đồ thị của hàm số ta dễ dàng thấy được:
Điểm cực tiểu $\left( { - 1; - 4} \right),\left( {1; - 4} \right)$ và điểm cực đại $\left( {0; - 3} \right)$
Xét Đáp án A: $y' = 4{x^3} - 4x = 4x\left( {{x^2} - 1} \right)$ có các nghiệm $x = 0;x = \pm 1$.
Do đó đồ thị có các điểm cực tiểu là $\left( { - 1; - 4} \right),\left( {1; - 4} \right)$ và điểm cực đại là $\left( {0; - 3} \right)$.
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
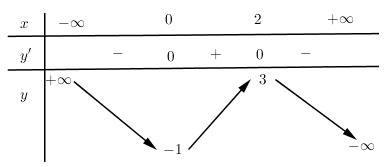
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Nhận xét: Dễ thấy bảng biến thiên của đồ thị hàm số bậc 3 nên loại đáp án B.
Ngoài cùng bên phải của $y< 0 \Rightarrow a < 0$ nên loại đáp án A.
Thay lần lượt hai điểm $\left( {0;\, - 1} \right)$ và $\left( {2;\,3} \right)$ vào 2 hàm số còn lại.
Thay $x = 0$ vào cả hai hàm số $y = - {x^3} + 3{x^2} - 1$ và $y = - {x^3} - 3{x^2} - 1$ ta thu được $y = - 1$ $ \Rightarrow \left( {0;\, - 1} \right)$ đều thuộc vào 2 đồ thị hàm số $y = - {x^3} + 3{x^2} - 1$ và $y = - {x^3} - 3{x^2} - 1$
Thay $x = 2$ vào hàm số $y = - {x^3} + 3{x^2} - 1$ ta được $ y = 3 \Rightarrow \left( {2;\,3} \right)$ thuộc vào đồ thị hàm số $y = - {x^3} + 3{x^2} - 1$.
Thay $x = 2$ vào hàm số $y = - {x^3} - 3{x^2} - 1$ ta được $y = - 21$ $ \Rightarrow \left( {2;\,3} \right)$ không thuộc vào đồ thị hàm số $y = - {x^3} - 3{x^2} - 1$.
Cho hàm số $y = f\left( x \right)$ xác định, liên tục trên $R$ có bảng biến thiên:
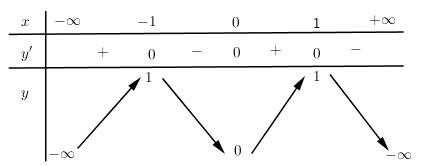
Bảng biến thiên trên là bảng biến thiên của hàm số nào?
Nhận xét: Dễ thấy bảng biến thiên của đồ thị hàm số bậc 4.
Ngoài cùng bên phải của $y' < 0 \Rightarrow a < 0 \Rightarrow $Loại đáp án A
Thay điểm $\left( {0;0} \right)$ vào các hàm số ở đáp án B, C, D
Điểm $\left( {0;0} \right)$ chỉ thuộc vào đồ thị hàm số $y = - {x^4} + 2{x^2}$
Cho hàm số $y = f\left( x \right) = a{x^4} + {b^2}{x^2} + 1\left( {a \ne 0} \right)$ . Trong các khẳng định dưới đây, khẳng định nào là đúng?
Ta có: $y' = 4a{x^3} + 2{b^2}{x}$
Dễ thấy $x = 0$ luôn là nghiệm của $y'$.
Mà hàm bậc 4 luôn có cực trị
$ \Rightarrow $ đáp án D đúng
Cho hàm số $y = f\left( x \right)$ có bảng biến thiên như sau:
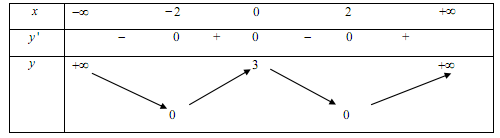
Khẳng định nào sau đây là khẳng định đúng?
A sai vì hàm số chỉ nghịch biến trên các khoảng $\left( { - \infty ; - 2} \right)$ và $\left( {0;2} \right)$
B sai vì hàm số đạt giá trị cực đại là $y = 3$ tại $x = 0$
C đúng vì từ bảng biến thiên ta thấy:
$\mathop {\min }\limits_R f\left( x \right) = 0 \Rightarrow f\left( x \right) \geqslant 0,\forall x \in R$
D sai vì hàm số chỉ đồng biến trên khoảng $\left( { - 2;0} \right)$ và $\left( {2; + \infty } \right)$
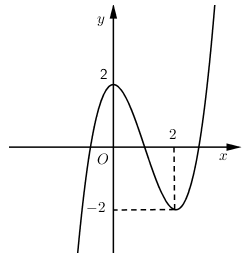
Cho hàm số $y = f\left( x \right)$ có đồ thị như hình vẽ. Khẳng định nào sau đây là đúng?
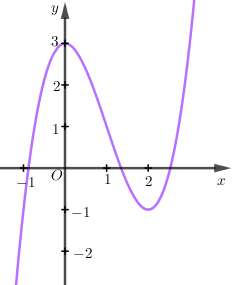
A sai vì $y=3$ là giá trị cực đại của hàm số, không phải giá trị lớn nhất.
B sai vì hàm số đồng biến trên các khoảng $\left( { - \infty ;0} \right),\left( {2; + \infty } \right)$.
C sai vì $x=2$ là điểm cực tiểu của hàm số không phải giá trị cực tiểu.
D đúng vì trên đoạn $\left[ {0;4} \right]$ thì hàm số đạt GTNN (cũng là giá trị cực tiểu) bằng $ - 1$ đạt được tại $x = 2$.
Cho hàm số $y = a{x^3} + b{x^2} + cx + d\,\left( {a \ne 0} \right)$ có đồ thị hàm số như hình vẽ dưới đây. Khẳng định nào sau đây về dấu của $a,b,c,d$ là đúng nhất?
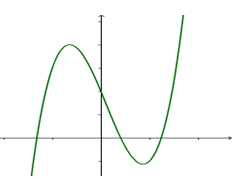
$\mathop {\lim }\limits_{x \to - \infty } x = - \infty $ nên $a > 0$
Dựa vào đồ thị hàm số ta có $y' = 3a{x^2} + 2bx + c = 0$ có hai nghiệm phân biệt trái dấu
$ \Rightarrow ac < 0$ mà $a > 0$ nên suy ra $c < 0$ suy ra loại B, C.
Mặt khác thấy đồ thị cắt trục $Oy$ tại điểm có tung độ dương $ \Rightarrow d > 0$
Hàm số $y = a{x^3} + b{x^2} + cx + d$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây là đúng?
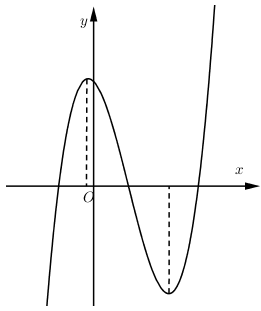
Nhận xét: Hàm số bậc 3 có $2$ cực trị và hệ số $a > 0$
Khi $x = 0 \Leftrightarrow y = d > 0$
$y' = 3a{x^2} + 2bx + c$ có $2$ nghiệm phân biệt trái dấu $\Leftrightarrow 3ac < 0 \Leftrightarrow c < 0$ (Vì $a > 0$)
$\dfrac{{{x_1} + {x_2}}}{2} > 0 \Leftrightarrow \dfrac{{\dfrac{{ - 2b}}{{3a}}}}{2} > 0 \Leftrightarrow \dfrac{{ - b}}{{3a}} > 0 \Rightarrow - b > 0\,(Do\,a > 0) \Rightarrow b < 0$
Vậy khẳng định đúng là: $a > 0, b < 0, c < 0, d > 0$
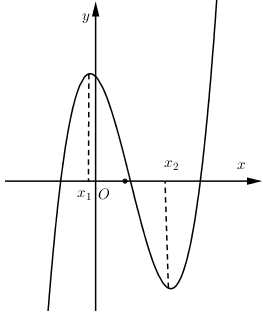
Hàm số $y = a{x^4} + b{x^2} + c$ có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
Nhận xét: Hàm số bậc 4 trùng phương có $3$ cực trị và hệ số $a > 0$
Từ đồ thị ta có: $x = 0 $ thì $y = c < 0$
Hàm số có $3$ cực trị thì $ab < 0$ suy ra $b < 0$ (vì $a > 0$)
Vậy khẳng định đúng là: $ a > 0, b < 0, c < 0$
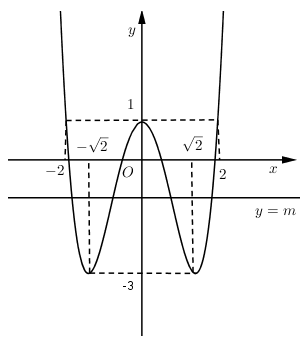
Đồ thị hàm số bên là đồ thị của hàm số $y = {x^4} - 4{x^2} + 1\left( C \right).$ Tìm $m$ để phương trình ${x^4} - 4{x^2} + 1 - m = 0$ có $4$ nghiệm phân biệt
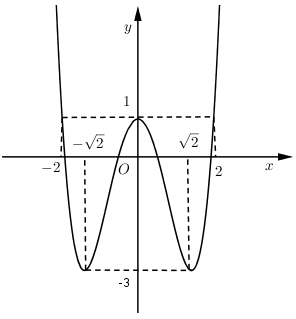
${x^4} - 4{x^2} + 1 - m = 0 \Leftrightarrow {x^4} - 4{x^2} + 1 = m$
Số nghiệm của phương trình ${x^4} - 4{x^2} + 1 - m = 0$ là số giao điểm của đồ thị hàm số $y = {x^4} - 4{x^2} + 1$ và đường thẳng $y = m$.
Þ Để phương trình ${x^4} - 4{x^2} + 1 - m = 0$ có $4$ nghiệm phân biệt $ \Leftrightarrow - 3 < m < 1$
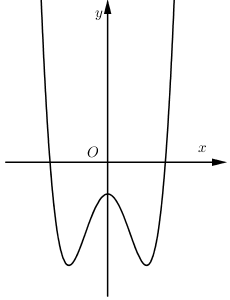
Cho hàm số $y = - {x^4} + 2{{\text{x}}^2} + 1$ có đồ thị như hình dưới. Tìm tất cả các giá trị thực của tham số $m$ để phương trình $ - {x^4} + 2{{\text{x}}^2} + 1 = m$ có bốn nghiệm phân biệt.
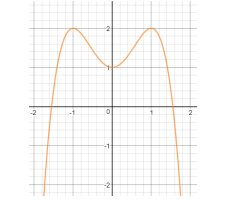
Xét : $ - {x^4} + 2{{\text{x}}^2} + 1 = m$
Số nghiệm của phương trình bằng số giao điểm của đồ thị hai hàm số $y = - {x^4} + 2{{\text{x}}^2} + 1;y = m$
Nhìn đồ thị chọn D.
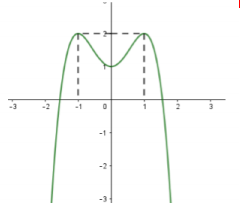
Cho hàm số \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên sau:
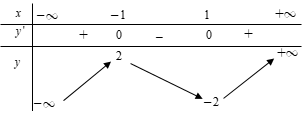
Đồ thị nào trong các phương án A, B, C, D thể hiện hàm số \(y = f\left( x \right)\)?
Dựa vào bảng biến thiên, ta thấy:
- Khi \(x \to + \infty \) thì \(y \to + \infty \). Loại C và D.
- Tọa độ các điểm cực trị là \(\left( { - 1;2} \right)\) và \(\left( {1; - 2} \right)\) nên đáp án A là phù hợp.
Cho các dạng đồ thị (I), (II), (III) như hình dưới đây:
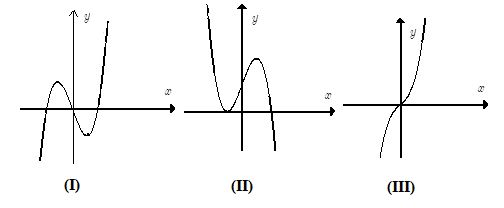
Liệt kê tất cả các dạng có thể biểu diễn đồ thị hàm số \(y = {x^3} + b{x^2} - x + d\).
Chào em, ta quan sát đồ thị 3 sẽ thấy, đồ thị này không có điểm cực trị
=> $b^2-3ac<0$
Mà với hàm số bài cho thì $b^2-3ac=b^2+3>0$ với mọi b
Hàm số \(y = {x^3} + b{x^2} - x + d\) có hệ số của \({x^3}\) dương nên loại (II).
Xét \(y' = 3{x^2} + 2bx - 1\) có \(\Delta ' = {b^2} + 3 > 0,\forall b \in \mathbb{R}\).
Do đó hàm số có hai cực trị.
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có bảng biến thiên như hình bên. Trong các hệ số a, b, c và d có bao nhiêu số âm?
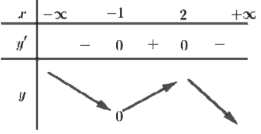
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = - \infty \Rightarrow a < 0\).
\(y' = 3a{x^2} + 2bx + c\).
Dựa vào BBT ta thấy hàm số có hai điểm cực trị \({x_1} = - 1,\,\,{x_2} = 2\) nên phương trình \(y' = 0\) có hai nghiệm phân biệt thỏa mãn \(S = {x_1} + {x_2} = 1 > 0\), \(P = {x_1}{x_2} = - 2 < 0\) \( \Rightarrow \left\{ \begin{array}{l}\Delta ' = {b^2} - 3ac > 0\\S = \dfrac{{ - 2b}}{{3a}} > 0\\P = \dfrac{c}{{3a}} < 0\end{array} \right.\).
Mà \(a < 0\) nên \(b > 0\) và \(c > 0\).
Dựa vào BBT ta thấy tại điểm \(x = 0\) thì \(y > 0\), do đó \(d > 0\).
Vậy trong 4 hệ số a, b, c, d chỉ có 1 số âm.
Cho đồ thị (C) của hàm số \(y = {x^3} - 6{x^2} + 9x - 1\) như hình vẽ. Hãy xác định số điểm cực trị của hàm số \(y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1\).
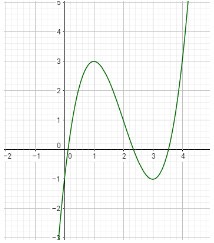
Từ đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x - 1\) ta suy ra được đồ thị hàm số \(y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1\) như sau (phần nét liền):
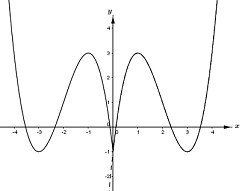
Dựa vào đồ thị hàm số ta thấy hàm số \(y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1\) có 5 điểm cực trị.
Biết rằng hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị là đường cong như hình vẽ bên dưới.
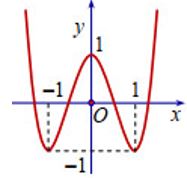
Tính giá trị \(f\left( {3a + 2b + c} \right)\).
Ta có \(f'\left( x \right) = 4a{x^3} + 2bx\).
Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số đi qua các điểm \(\left( {0;1} \right);\,\,\left( {1; - 1} \right)\).
Đồng thời đây cũng là 2 điểm cực trị của hàm số. Do đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}f\left( 0 \right) = 1\\f\left( 1 \right) = - 1\\f'\left( 1 \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a + b + c = - 1\\4a + 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a = 2\\b =- 4\end{array} \right.\).
\( \Rightarrow f\left( x \right) = 2{x^4} - 4{x^2} + 1\) và \(3a + 2b + c = 3.2 + 2.(-4) + 1 = -1\).
Vậy \(f\left( {3a + 2b + c} \right) = f\left( -1 \right) = - 1\).
Cho hàm số \(f\left( x \right) = a{x^4} + b{x^3} + c{x^2} + dx + e,\) với \(a,b,c,d,e \in \mathbb{R}.\) Hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
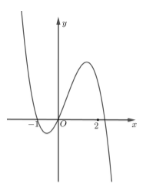
Ta có \(f'\left( x \right) = 4a{x^3} + 3b{x^2} + 2cx + d\)
Từ đồ thị hàm số ta thấy \(f'\left( 0 \right) \Leftrightarrow d = 0\)
Từ đồ thị ta thấy:
+ Khi $x< -1$ thì $f'(x)>0$.
+ Khi $-1<x<0=>f'(x)<0$
+ Khi $0<x<x_0$ (với $x_0$ là nghiệm thứ 3 của phương trình $f'(x)=0$) $=>f'(x)>0$
+ Khi $x>x_0$ thì $f'(x)<0$
Ta có bảng biến thiên:
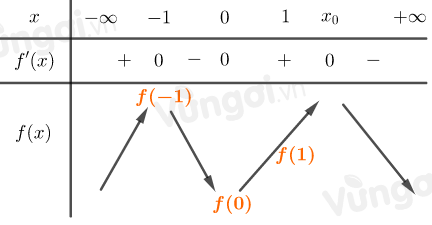
\(\Rightarrow f\left( { - 1} \right) > f\left( 0 \right)\)
\( \Leftrightarrow a - b + c - d + e > e \Leftrightarrow a + c > b + d\) nên B sai, lại có \(d = 0 \Rightarrow a + c > b\) (1)
+) Từ bảng biến thiên \( \Rightarrow f\left( 1 \right) > f\left( 0 \right)\)
\( \Leftrightarrow a + b + c + d + e > e \Leftrightarrow a + b + c + d > 0\) nên A sai.
Mà \(d = 0\) nên \(a + b + c > 0 \Leftrightarrow a + c > - b\) (2)
Từ (1) và (2) suy ra \(2\left( {a + c} \right) > 0 \Leftrightarrow a + c > 0.\)