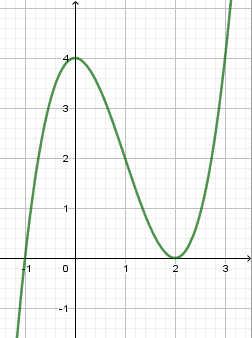
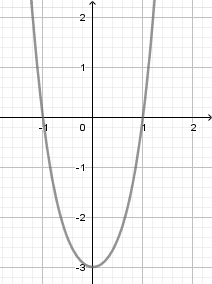
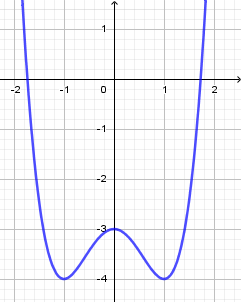
Cho các dạng đồ thị (I), (II), (III) như hình dưới đây:

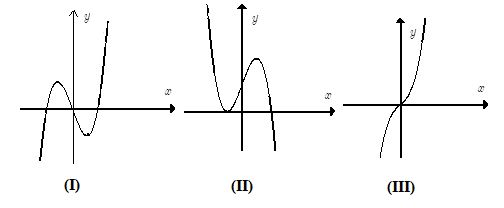
Liệt kê tất cả các dạng có thể biểu diễn đồ thị hàm số \(y = {x^3} + b{x^2} - x + d\).

Chào em, ta quan sát đồ thị 3 sẽ thấy, đồ thị này không có điểm cực trị

=> $b^2-3ac<0$

Mà với hàm số bài cho thì $b^2-3ac=b^2+3>0$ với mọi b

$y =  - {x^3} + x + 2$ 

$y = {x^3} - 3{x^2} + 2$ 

$y = {x^4} - {x^2} + 1$ 

$y = {x^3} - 3x + 2$

$y = {x^3} - 2{x^2} + x - 2$   

$y = \left( {x + 1} \right){\left( {x - 2} \right)^2}$

$y = \left( {x - 1} \right){\left( {x - 2} \right)^2}$      

$y = {x^3} + 3{x^2} - x - 1$

$y =  - {x^4} - 2{x^2} + 3$

$y = {x^4} - 2{x^2} - 3$         

$y =  - {x^4} - 2{x^2} - 3$

$y = {x^4} + 2{x^2} - 3$

$y = {x^4} - 2{x^2} - 3$

$y =  - \dfrac{1}{4}{x^4} + 3{x^2} - 3$

$y = {x^4} - 3{x^2} - 3$

$y = {x^4} + 2{x^2} - 3$

$y = {x^3} + 2{x^2} - 5$        

$y = {x^4} + 2{x^2} - 3$ 

$y =  - {x^3} + 3{x^2} - 1$ 

$y =  - {x^3} - 3{x^2} - 1$

$y = {x^4} - 2{x^2}$ 

$y =  - {x^4} + 2{x^2}$          

$y =  - {x^4} - 2{x^2} - 3$ 

$y =  - {x^4} - 2{x^2} + 1$

Hàm số nhận gốc tọa độ làm tâm đối xứng

Hàm số nhận trục hoành làm trục đối xứng

Với $a > 0$, đồ thị hàm số có ba điểm cực trị luôn tạo thành một tam giác cân

Với mọi giá trị của tham số $a,b\left( {a \ne 0} \right)$ thì hàm số luôn có cực trị