Khoảng cách từ một điểm đến đường thẳng
Kỳ thi ĐGTD ĐH Bách Khoa
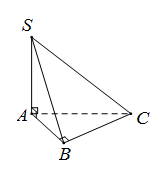
Cho hình chóp $S.ABC$ trong đó $SA,{\rm{ }}AB,{\rm{ }}BC$ đôi một vuông góc và $SA = AB = BC = 1.$ Khoảng cách giữa hai điểm $S$ và $C$ nhận giá trị nào trong các giá trị sau ?
Do $\left\{ \begin{array}{l}SA \bot AB\\SA \bot BC\end{array} \right.$ nên $SA \bot (ABC) \Rightarrow SA \bot AC$
Như vậy \(SC = \sqrt {S{A^2} + A{C^2}} = \sqrt {S{A^2} + A{B^2} + B{C^2}} = \sqrt 3 \)
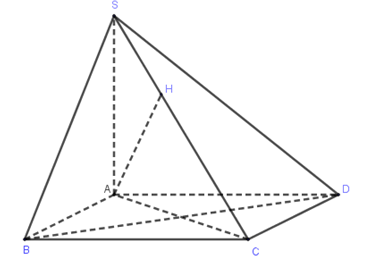
Cho tứ diện $SABC$ trong đó$SA$, $SB$, $SC$ vuông góc với nhau từng đôi một và$SA = 3a$, $SB = a$,$SC = 2a$. Khoảng cách từ $A$ đến đường thẳng $BC$ bằng:
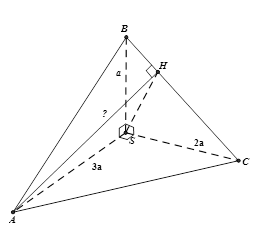
+ Dựng $AH \bot BC$ $ \Rightarrow d\left( {A,BC} \right) = AH$.
+ $\left\{ \begin{array}{l}AS \bot \left( {SBC} \right) \supset BC \Rightarrow AS \bot BC\\AH \bot BC\end{array} \right.$, $AH$cắt $AS$ cùng nằm trong $\left( {SAH} \right)$.
$ \Rightarrow BC \bot \left( {SAH} \right) \supset SH \Rightarrow BC \bot SH$.
Xét trong $\Delta SBC$ vuông tại $S$ có $SH$ là đường cao ta có:
$\dfrac{1}{{S{H^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{S{C^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{4{a^2}}} = \dfrac{5}{{4{a^2}}}$ $ \Rightarrow S{H^2} = \dfrac{{4{a^2}}}{5}$ $ \Rightarrow SH = \dfrac{{2a\sqrt 5 }}{5}$.
+ Ta dễ chứng minh được $AS \bot \left( {SBC} \right) \supset SH \Rightarrow AS \bot SH$ $ \Rightarrow \Delta ASH$ vuông tại $S$.
Áp dụng định lý Pi-ta-go cho $\Delta ASH$ vuông tại $S$ta có:
$A{H^2} = S{A^2} + S{H^2} = 9{a^2} + \dfrac{{4{a^2}}}{5} = \dfrac{{49{a^2}}}{5}$ $ \Rightarrow AH = \dfrac{{7a\sqrt 5 }}{5}$.
Cho hình chóp $A.BCD$ có cạnh $AC \bot \left( {BCD} \right)$ và $BCD$ là tam giác đều cạnh bằng $a$. Biết $AC = a\sqrt 2 $ và $M$ là trung điểm của $BD$. Khoảng cách từ $C$ đến đường thẳng $AM$ bằng
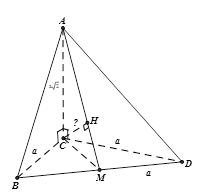
Dựng $CH \bot AM \Rightarrow d\left( {C,AM} \right) = CH$ .
Vì $\Delta BCD$ là tam giác đều cạnh $a$ và $M$ là trung điểm của $BD$ nên dễ tính được $CM = \dfrac{{a\sqrt 3 }}{2}$.
Xét $\Delta ACM$ vuông tại $C$ có $CH$ là đường cao, ta có:
$\begin{array}{l}\dfrac{1}{{C{H^2}}} = \dfrac{1}{{C{A^2}}} + \dfrac{1}{{C{M^2}}} = \dfrac{1}{{2{a^2}}} + \dfrac{1}{{\dfrac{{3{a^2}}}{4}}} = \dfrac{{11}}{{6{a^2}}}\\ \Rightarrow C{H^2} = \dfrac{{6{a^2}}}{{11}} \Rightarrow CH = a\sqrt {\dfrac{6}{{11}}} \end{array}$
Hình chóp đều $S.ABC$ có cạnh đáy bằng $3a,$ cạnh bên bằng $2a$. Gọi \(H\) là trung điểm của \(BC\), khoảng cách từ $S$ đến \(AH\) bằng:
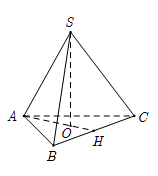
Gọi \(O\) là chân đường cao của hình chóp nên \(O\) là tâm tam giác đáy.
Do đó \(O\) là trọng tâm tam giác \(ABC\) hay \(O \in AH\)
Ta có \(AO = \dfrac{2}{3}AH = \dfrac{2}{3}.3a.\dfrac{{\sqrt 3 }}{2} = a\sqrt 3 \)
${\rm{d}}\left( {S,AH} \right) = SO = \sqrt {S{A^2} - A{O^2}} = a$
Cho hình chóp $A.BCD$có cạnh $AC \bot \left( {BCD} \right)$và $BCD$ là tam giác đều cạnh bằng $a$. Biết $AC = a\sqrt 2 $, khoảng cách từ $A$ đến đường thẳng $BD$ bằng:
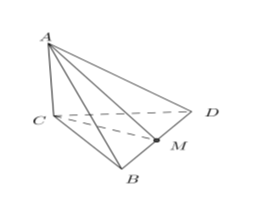
Gọi \(M\) là trung điểm của \(BD\).
Ta có: $\left\{ \begin{array}{l}AC \bot BD\\CM \bot BD\end{array} \right. \Rightarrow BD \bot AM$ (Định lý 3 đường vuông góc) $ \Rightarrow d\left( {A;BD} \right) = AM$.
$CM = \dfrac{{a\sqrt 3 }}{2}$ (vì tam giác $BCD$ đều).
Ta có: $AM = \sqrt {A{C^2} + M{C^2}} = \sqrt {2{a^2} + \dfrac{{3{a^2}}}{4}} = \dfrac{{a\sqrt {11} }}{2}$.
Cho hình chóp $S.ABCD$có $SA \bot \left( {ABCD} \right)$, đáy $ABCD$ là hình thoi cạnh bằng $a$ và $\hat B = 60^\circ $. Biết $SA = 2a$. Tính khoảng cách từ $A$ đến $SC$.
Kẻ $AH \bot SC$, khi đó $d\left( {A,SC} \right) = AH$.
$ABCD$ là hình thoi cạnh bằng $a$ và $\hat B = 60^\circ \Rightarrow \Delta ABC$ đều nên $AC = a$.
Trong tam giác vuông $SAC$ta có:
$\dfrac{1}{{A{H^2}}} = \dfrac{1}{{S{A^2}}} + \dfrac{1}{{A{C^2}}}$
$ \Rightarrow AH = \dfrac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{2a.a}}{{\sqrt {4{a^2} + {a^2}} }} = \dfrac{{2\sqrt 5 a}}{5}$.
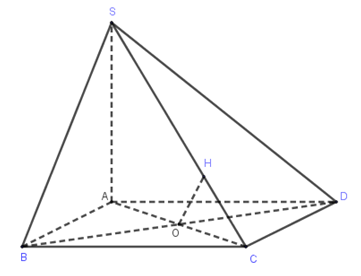
Cho hình chóp $S.ABCD$ có $SA \bot \left( {ABCD} \right)$, $SA = 2a$, $ABCD$ là hình vuông cạnh bằng $a$. Gọi $O$ là tâm của $ABCD$, tính khoảng cách từ $O$ đến $SC$.
Kẻ $OH \bot SC$, khi đó $d\left( {O,SC} \right) = OH$. Ta có: $\Delta SAC \sim \Delta OHC(g-g)$ nên $\dfrac{{OH}}{{SA}} = \dfrac{{OC}}{{SC}} \Rightarrow OH = \dfrac{{OC}}{{SC}}.SA$.
Mà: $OC = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2},SC = \sqrt {S{A^2} + A{C^2}} = a\sqrt 6 $
Vậy $OH = \dfrac{{OC}}{{SC}}.SA = \dfrac{a}{{\sqrt 3 }} = \dfrac{{a\sqrt 3 }}{3}$
Cho hình chóp tứ giác đều có cạnh đáy bằng $a$ và góc hợp bởi một cạnh bên và mặt đáy bằng $\alpha $. Khoảng cách từ tâm của đáy đến một cạnh bên bằng
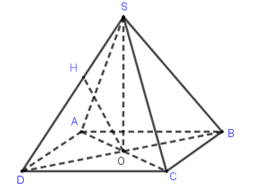
$SO \bot \left( {ABCD} \right)$, $O$ là tâm của hình vuông $ABCD$.
Kẻ $OH \bot SD$, khi đó $d\left( {O;SD} \right) = OH,\alpha = \widehat {SDO}$
$OD = \dfrac{1}{2}BD = \dfrac{{a\sqrt 2 }}{2}$ $ \Rightarrow OH = OD\sin \alpha = \dfrac{{a\sqrt 2 \sin \alpha }}{2}$.
Cho hình chóp $S.ABC$ trong đó $SA$, $AB$, $BC$ vuông góc với nhau từng đôi một. Biết $SA = 3a$, $AB = a\sqrt 3 $, $BC = a\sqrt 6 $. Khoảng cách từ $B$ đến $SC$ bằng
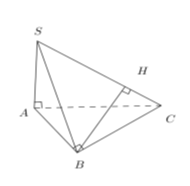
Vì $SA,AB,BC$ vuông góc với nhau từng đôi một nên $CB \bot SB$.
Kẻ $BH \bot SC$, khi đó $d\left( {B;SC} \right) = BH$.
Ta có: $SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {9{a^2} + 3{a^2}} = 2\sqrt 3 a$.
Trong tam giác vuông $SBC$ ta có:
$\dfrac{1}{{B{H^2}}} = \dfrac{1}{{S{B^2}}} + \dfrac{1}{{B{C^2}}} \Rightarrow BH = \dfrac{{SB.BC}}{{\sqrt {S{B^2} + B{C^2}} }} = 2a$.
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Khoảng cách từ đỉnh \(A\) của hình lập phương đó đến đường thẳng \(CD'\) bằng
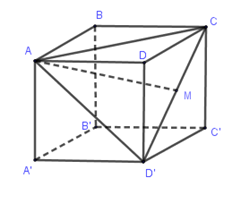
Gọi $M$ là trung điểm của $CD'$. Do \(ABCD.A'B'C'D'\)là hình lập phương nên tam giác $ACD'$là tam giác đều cạnh \(a\sqrt 2 \).
$AM \bot CD' \Rightarrow d\left( {A,CD'} \right) = AM = \dfrac{{a\sqrt 6 }}{2}$
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a.\) Khoảng cách từ đỉnh \(A\) của hình lập phương đó đến đường thẳng \(DB'\) bằng
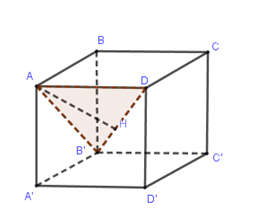
Gọi $H$là chân đường vuông góc hạ từ $A$ xuống $DB'$.
Dễ thấy $AD \bot \left( {ABB'A'} \right) \Rightarrow \Delta ADB'$vuông đỉnh $A$.
Lại có $AD = a;AB' = a\sqrt 2 \Rightarrow \dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{D^2}}} + \dfrac{1}{{AB{'^2}}} \Rightarrow AH = \dfrac{{a\sqrt 6 }}{3}$
Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng \(a\). Khoảng cách từ ba điểm nào sau đây đến đường chéo \(AC'\) bằng nhau ?
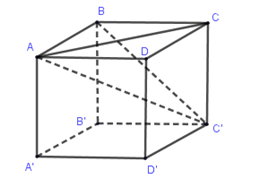
Dễ thấy các tam giác $ABC',C'CA,ADC'$ là các tam giác vuông bằng nhau nên các đường cao hạ từ đỉnh góc vuông xuống cạnh huyền cũng bằng nhau.
Vậy: $d\left( {B,AC'} \right) = d\left( {C,AC'} \right) = d\left( {D,AC'} \right)$

