Người ta thả một viên billiards snooker có dạng hình cầu với bán kính nhỏ hơn 4,5cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5cm. Bán kính của viên billiards đó bằng
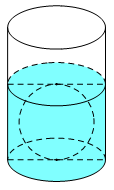
Thể tích mực nước ban đầu là: V1=πr21h1=π.5,42.4,5
Gọi R là bán kính của viên bi ta có sau khi thả viên bi vào cốc, chiều cao của mực nước bằng 2R, do đó tổng thể tích của nước và bi sau khi thả viên bi vào trong cốc là: V=πr21.(2R)=π.5,42.2R
Thể tích của quả cầu là: V(C)=43πR3
Ta có: V=V1+V2⇔5,42.4,5+43R3=5,42.2R
Giải phương trình trên với điều kiện R<4,5⇒R=2,7cm.
Có 4 viên bi hình cầu bán kính bằng 1cm. Người ta đặt 3 viên bi tiếp xúc nhau và cùng tiếp xúc với mặt bàn. Sau đó đai 3 viên bi đó lại và đặt 1 viên bi thứ 4 tiếp xúc vởi cả 3 viên bi trên như hình vẽ bên dưới. Gọi O là điểm thuộc bề mặt của viên bi thứ 4 có khoảng cách đến mặt bàn là lớn nhất. Khoảng cách từ O đến mặt bàn bằng
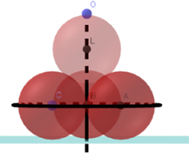
Tứ diện đều ABCD có cạnh đều bằng 2 (do BC=BM+MC=1+1=2).
Tam giác ACD đều, cạnh bằng 2 => Chiều cao AN=2.√32=√3
Tam giác BCD đều, cạnh bằng 2, I là trọng tâm
=> IN=13BN=13.√3=√33
Tam giác AIN vuông tại I, theo Pytago ta có: AI=√AN2−IN2=√(√3)2−(√33)2=√83=√243=2√63
Vậy, khoảng cách từ O đến mặt bàn bằng OJ=OA+AI+IJ=1+ 2√63 +1= 6+2√63
Một hộp đựng phấn hình hộp chữ nhật có chiều dài 30cm, chiều rộng 5cm và chiều cao 6cm. Người ta xếp thẳng đứng vào đó các viên phấn giống nhau, mỗi viên phấn là khối trụ có chiều cao h=6cm và bán kính đáy r=12cm. Hỏi có thể xếp được tối đa bao nhiêu viên phấn.
Đường kính đường tròn đáy của một viên phấn là d=2r=2.12=1(cm) .
Chiều rộng của hộp là 5cm ⇒ Xếp được tối đa 5 viên phấn theo chiều rộng.
Chiều dài của hộp là 30cm ⇒ Xếp được tối đa 30 viên phấn theo chiều dài.
Như vây, có thể xếp được tối đa 5×30=150 viên phấn vào hộp.
Cho hình chóp tam giác S.ABC có ^SAC=^SBC=900. Khi đó tâm mặt cầu ngoại tiếp hình chóp nằm trên đường thẳng nào?
Ta thấy: ^SAC=^SBC=900 nên các đỉnh A,B luôn nhìn cạnh SC một góc 900. Do đó tâm mặt cầu ngoại tiếp hình chóp là trung điểm SC.
Cho hình chóp đều S.ABCD có cạnh đáy bằng a, cạnh bên b. Công thức tính bán kính mặt cầu ngoại tiếp khối chóp là:
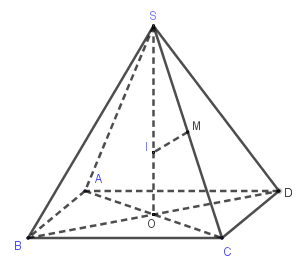
Ta có: ABCD là hình vuông cạnh a nên AC=a√2⇒OA=AC2=a√22
Tam giác SOC vuông tại O nên SC2=SO2+OC2⇒h=SO=√SC2−OC2=√b2−a22
Vậy R=b22h=b22√b2−a22
Công thức tính bán kính mặt cầu ngoại tiếp hình chóp có cạnh bên vuông góc với đáy là:
Hình chóp có cạnh bên vuông góc với đáy nội tiếp mặt cầu có bán kính R=√r2+h24, với r là bán kính đường tròn đáy, h là chiều cao hình chóp (độ dài cạnh bên vuông góc với đáy).
Công thức tính diện tích mặt cầu là:
Công thức tính diện tích mặt cầu S=4πR2
Hai quả bóng hình cầu có kích thước khác nhau được đặt ở hai góc của một căn nhà hình hộp chữ nhật sao cho mỗi quả bóng đều tiếp xúc với hai bức tường và nền của nhà đó. Biết rằng trên bề mặt của quả bóng đều tồn tại một điểm có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng 1,2,4. Tổng độ dài đường kính của hai quả bóng đó.
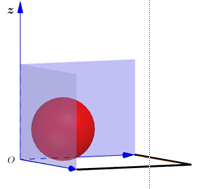
Xét quả bóng tiếp xúc với các bức tường và chọn hệ trục Oxyz như hình vẽ bên (tương tự với góc tường còn lại).
Gọi I(a;a;a) là tâm của mặt cầu (tâm quả bóng) và R=a.
⇒ phương trình mặt cầu của quả bóng là
(S):(x−a)2+(y−a)2+(z−a)2=a2(1).
Giả sử M(x;y;z) nằm trên mặt cầu (bề mặt của quả bóng) sao cho d(M;(Oxy))=1,d(M;(Oyz))=2,d(M;(Oxz))=3
Khi đó z=1;x=2;y=3⇒M(2;3;1)∈(S)(2).
Từ (1),(2) suy ra (1−a)2+(2−a)2+(4−a)2=a2
⇒{R1=a1=7−√72R2=a2=7+√72⇒d1+d2=2(R1+R2)=14.
Khối cầu thể tích V thì bán kính là:
Ta có: thể tích khối cầu V=43πR3⇒R=3√3V4π
Ba đoạn thẳng SA,SB,SC đôi một vuông góc tạo với nhau thành một tứ diện SABC với SA=a,SB=2a,SC=3a . Tính bán kính mặt cầu ngoại tiếp hình tứ diện đó là
Bán kính mặt cầu ngoại tiếp tứ diện vuông S.ABC được tính theo công thức
R=√SA2+SB2+SC24=√a2+(2a)2+(3a)22=a√142
Hình chóp S.ABC có đáy ABC là tam giác vuông tại A có SA vuông góc với mặt phẳng (ABC) và có SA=a,AB=b,AC=c. Mặt cầu đi qua các đỉnh A,B,C,S có bán kính r bằng :
Vì SA⊥(ABC)⇒{SA⊥ABSA⊥AC.
Mà AB⊥AC nên hình chóp S.ABC là tứ diện vuông.
Áp dụng công thức tính bán kính mặt cầu ngoại tiếp tứ diện vuông ta được R=√a2+b2+c24=√a2+b2+c22
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 1, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp đã cho.
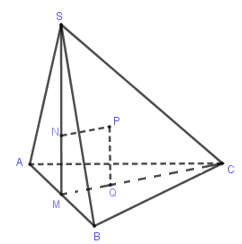
Gọi M,N,P,Q lần lượt là trung điểm AB, tâm đường tròn ngoại tiếp ΔSAB, tâm mặt cầu ngoại tiếp hình chóp và tâm đường tròn ngoại tiếp ΔABC⇒MNPQ là hình vuông suy ra
PN=MQ=13.√32=√36;NB=23.√32=√33
Bán kính mặt cầu ngoại tiếp chóp là R=PB=√PN2+NB2=√156
Thể tích V=43πR3=5√15π54
Cho hình chóp tam giác đều S.ABC có đáy ABC là tam giác đều cạnh a, cạnh SA=2a√33 . Gọi D là điểm đối xứng của B qua C. Tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABD
Do D đối xứng với C qua B nên có BC=DC=AC suy ra tam giác ABD là tam giác vuông tại A.
Kẻ đường thẳng d qua C vuông góc với đáy, đường thẳng này là trục đường tròn ngoại tiếp tam giác đáy ABD .
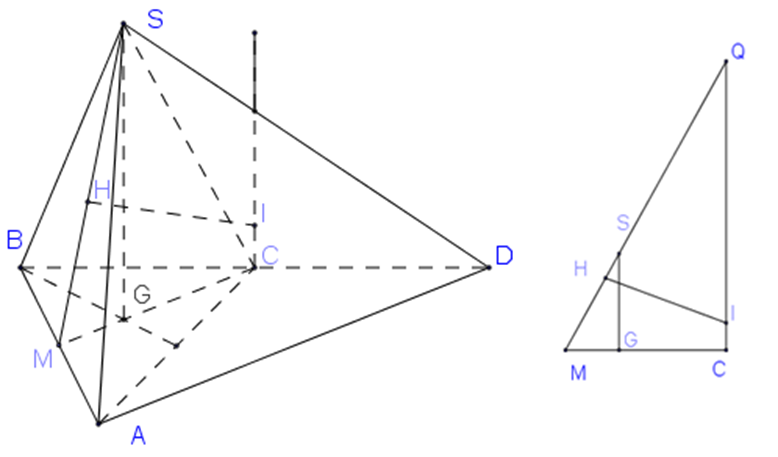
Tam giác SAB cân tại S , gọi M là trung điểm AB,H là tâm đường tròn ngoại tiếp tam giác SAB
⇒H∈SM;SM=√SA2−AM2=a√132√3
SH=AB.SA.SB4.SSAB=(2a√3)2.a4.12.a.AM=4a√39
Trong (SAC) dựngHI⊥SM(I∈d)(1).
Mà {AB⊥SMAB⊥MC⇒AB⊥(SMC)⇒AB⊥HI(2)
Từ (1), (2) suy ra HI⊥(SAB) , suy ra I là tâm đường tròn ngoại tiếp hình chóp S.ABD
Gọi Q=MS∩CI, xét tam giác SCM có
SMQM=MGMC=13 ⇒QM=3SM=3.a√132√3=a√392
⇒QH=QM−MS+HS =a√392−a√132√3+4a√39=17a√39
QC=√QM2−MC2=3a
Xét: ΔQHI∼ΔQCM⇒HICM=HQQC ⇒HI=HQ.CMQC=17a6√13
⇒R=SI=√HI2+HS2=√(a√176√13)2+(4a√39)2=a√376
Cho tứ diện đều ABCD có cạnh a. Một mặt cầu tiếp xúc với các mặt của tứ diện có bán kính là:
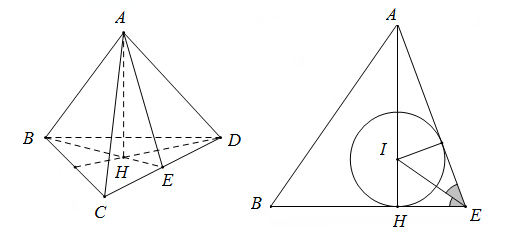
Gọi H là tâm tam giác đều BCD,E là trung điểm CD
Ta có AH \bot \left( {BCD} \right)
Gọi I,r là tâm và bán kính mặt cầu tiếp xúc với các mặt của tứ diện ABCD thì I là giao của AH và phân giác góc AEB của \Delta AEB. Ta có
\begin{array}{l}AE = BE = \dfrac{{a\sqrt 3 }}{2};HE = \dfrac{{BE}}{3} = \dfrac{{a\sqrt 3 }}{6}\\AH = \sqrt {A{E^2} - H{E^2}} = \dfrac{{a\sqrt 6 }}{3}\end{array}
Áp dụng tính chất đường phân giác:
\begin{array}{l}\dfrac{{IH}}{{IA}} = \dfrac{{EH}}{{EA}} \Rightarrow \dfrac{{IH}}{{IH + IA}} = \dfrac{{EH}}{{EH + EA}}\\ \Rightarrow r = IH = \dfrac{{EH.AH}}{{EH + EA}} = \dfrac{{a\sqrt 6 }}{{12}}\end{array}
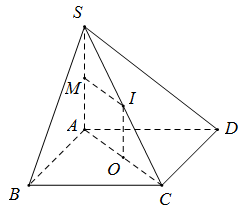
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a,\,AD = 2a, SA \bot \left( {ABCD} \right) và SA = 2a. Tính thể tích khối cầu ngoại tiếp hình chóp S.ABCD.
Gọi O là tâm hình chữ nhật ABCD,M và I lần lượt là trung điểm SA,SC \Rightarrow AOIM là hình chữ nhật.
Ta có O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD,OI \bot \left( {ABCD} \right) nên OI là trục đường tròn ngoại tiếp hình chữ nhật ABCD
IM \bot SA \Rightarrow IM là trung trực SA trong mặt phẳng \left( {SAC} \right)
\Rightarrow I là tâm mặt cầu ngoại tiếp hình chóp.
Có OI = AM = \dfrac{{SA}}{2} = a;OC = \dfrac{{AC}}{2} = \dfrac{1}{2}\sqrt {A{B^2} + A{D^2}} = \dfrac{{a\sqrt 5 }}{2}
Bán kính và thể tích mặt cầu lần lượt là
\begin{array}{l}R = IC = \sqrt {I{O^2} + O{C^2}} = \dfrac{{3a}}{2}\\V = \dfrac{4}{3}\pi {R^3} = \dfrac{{9\pi {a^3}}}{2}\end{array}
Cho lăng trụ đứng ABC.A'B'C' có đáy là tam giác vuông cân đỉnh A,AB = AC = a,AA' = a\sqrt 2 . Diện tích mặt cầu ngoại tiếp tứ diện CA'B'C' là:
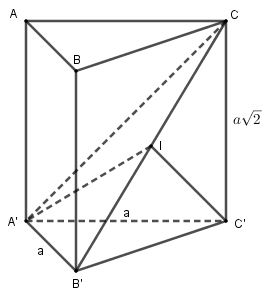
Ta có:
\begin{array}{l}A'B' = AB = a\\B'C' = \sqrt {A'B{'^2} + A'C{'^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \\B'C = \sqrt {B'C{'^2} + C'{C^2}} = \sqrt {2{a^2} + 2{a^2}} = 2a\\A'C = \sqrt {A'C{'^2} + C'{C^2}} = \sqrt {{a^2} + 2{a^2}} = a\sqrt 3 \\ \Rightarrow A'B{'^2} + A'{C^2} = {a^2} + 3{a^2} = 4{a^2} = B'{C^2}\end{array}
\Rightarrow \Delta A'B'C vuông tại A'.
Gọi I là trung điểm của B'C thì IB' = IC = IA'
Mà \Delta CC'B' vuông tại C' nên IB' = IC = IC'
Vậy I là tâm mặt cầu ngoại tiếp tứ diện CA'B'C' và bán kính R = \frac{1}{2}B'C = a.
\Rightarrow S = 4\pi {R^2} = 4\pi {a^2}.
Cho hình chóp S.ABC có SA \bot (ABC);AC = b,AB = c,\widehat {BAC} = \alpha . Gọi B',C' lần lượt là hình chiếu vuông góc của A lên SB,SC. Tính bán kính mặt cầu ngoại tiếp khối chóp A.{\rm{ }}BCC'B' theo b,c,\alpha
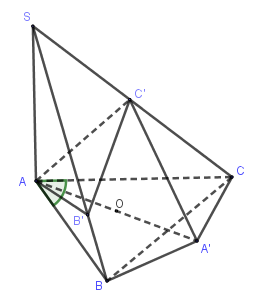
Gọi AA' là đường kính của đường tròn ngoại tiếp tam giác ABC
AC \bot A'C;\,AB \bot A'B
Ta chứng minh AC' \bot A'C'
SA \bot A'C;\,AC \bot A'C \Rightarrow A'C \bot AC'
Mà AC' \bot SC \Rightarrow AC' \bot A'C'
Tương tự AB' \bot A'B'
Như vậy B,C,C',B' cùng nhìn AA' bằng 1 góc vuông nên A,B,C,B',C' cùng thuộc 1 mặt cầu có đường kính là AA' và cũng đồng thời là đường kính của đường tròn ngoại tiếp tam giác ABC.
Tính BC = \sqrt {{b^2} + {c^2} - 2b\cos \alpha }
Trong tam giác ABC:\dfrac{{BC}}{{\sin A}} = 2R \Rightarrow R = \dfrac{{\sqrt {{b^2} + {c^2} - 2bc\cos \alpha } }}{{2\sin \alpha }}
Một hình hộp chữ nhật có độ dài ba cạnh lần lượt là 2;2;1. Tìm bán kính R của mặt cầu ngoại tiếp hình hộp chữ nhật trên.
Áp dụng công thức trên có R = \dfrac{3}{2}
Cho một mặt cầu bán kính bằng 1. Xét các hình chóp tam giác đều ngoại tiếp mặt cầu trên. Hỏi thể tích nhỏ nhất của chúng bằng bao nhiêu?
Áp dụng các công thức trong tứ diện đều cạnh a
Bán kính mặt cầu nội tiếp r = \dfrac{{a\sqrt 6 }}{{12}} = 1 \Rightarrow a = 2\sqrt 6
Thể tích tứ diện đều đó là V = \dfrac{{{a^3}\sqrt 2 }}{{12}} = 8\sqrt 3
Cho một lập phương có cạnh bằng a. Tính diện tích mặt cầu nội tiếp hình lập phương đó
Mặt cầu nội tiếp hình lập phương cạnh a có bán kính bằng \dfrac{a}{2}
Diện tích mặt cầu đó là S = 4\pi {R^2} = 4\pi {\left( {\dfrac{a}{2}} \right)^2} = \pi {a^2}

