Các hàm số lượng giác

Hàm $y = \sin x$ có TXĐ $D = R$.

Hàm số $y = \sin x$ có tập giá trị $\left[ { - 1;1} \right]$.

Hàm số $y = \cos x$ nghịch biến trên mỗi khoảng $\left( {k2\pi ;\pi  + k2\pi } \right)$

Nếu $x = 0$ thì $y = \tan 0 = 0$ nên điểm $O$ nằm trên đồ thị hàm số $y = \tan x$

B sai vì khi thay hoành độ của điểm M vào ta được $y=\tan x=\tan 0=0\ne 1$

C sai vì với $x=\dfrac{\pi}{2}$, không tồn tại $\tan \dfrac{\pi}{2}$

D sai vì với $x=1$ thì ta được $y=\tan 1 \ne 0$

Ta có: $-1 \le \sin \left( {2x - \dfrac{\pi }{4}} \right) \le 1$

$\begin{array}{l} \Rightarrow \sin \left( {2x - \dfrac{\pi }{4}} \right) \le 1 \\\Leftrightarrow 3.\sin \left( {2x - \dfrac{\pi }{4}} \right) \le 3.1\\ \Rightarrow y=1 + 3\sin \left( {2x - \dfrac{\pi }{4}} \right) \le 1 + 3 = 4\end{array}$

$\max y = 4$. Dấu "=" xảy ra khi $\sin \left( {2x - \dfrac{\pi }{4}} \right)=1$.

Ta có:

$\sin \left( {2x - \dfrac{\pi }{4}} \right) \ge  - 1$

$\Leftrightarrow 3.\sin \left( {2x - \dfrac{\pi }{4}} \right) \ge 3.\left( { - 1} \right)$

$\Rightarrow y = 1 + 3\sin \left( {2x - \dfrac{\pi }{4}} \right) \ge 1 + 3.(-1) =  - 2$

$\min y =  - 2$. Dấu "=" xảy ra khi $\sin \left( {2x - \dfrac{\pi }{4}} \right)=-1$.

Vậy $\max y = 4,\min y =  - 2$

Hàm số $y = \sin x$ và $y = \cos x$ có chu kì $T = 2\pi$.

Hàm số $y = \cot x$ và hàm số $y = \tan x$ có chu kì $T = \pi$.

Vậy chỉ có đáp án C đúng.

+) Tìm GTLN

$\begin{array}{l}{\sin ^2}x \ge 0 \Rightarrow 2{\sin ^2}x \ge 0\end{array}$$\Rightarrow 1 + 2{\sin ^2}x \ge 1$

Lấy nghịch đảo 2 vế bất đẳng thức ta được:

$\dfrac{1}{{1 + 2{{\sin }^2}x}} \le \dfrac{1}{1}=1$

Nhân 2 vế với 4 ta được:

$\Rightarrow \dfrac{4}{{1 + 2{{\sin }^2}x}} \le 4.1 = 4\\\Rightarrow y \le 4$

Dấu “=” xảy ra khi ${\sin ^2}x = 0 \Leftrightarrow\sin x = 0$.

+) Tìm GTNN

$\begin{array}{l}{\sin ^2}x \le 1 \Rightarrow 2{\sin ^2}x \le 2\\\Rightarrow 1 + 2{\sin ^2}x \le 1 + 2 = 3\end{array}$

Lấy nghịch đảo 2 vế bất đẳng thức ta được:

$\dfrac{1}{{1 + 2{{\sin }^2}x}} \ge \dfrac{1}{3}$

Nhân 2 vế với 4 ta được:

$\Rightarrow \dfrac{4}{{1 + 2{{\sin }^2}x}} \ge \dfrac{4}{3}\\\Rightarrow y \ge \dfrac{4}{3}$

Dấu “=” xảy ra khi ${\sin ^2}x= 1\Leftrightarrow\sin x =  \pm 1$.

Vậy GTLN là 4, GTNN là $\dfrac{4}{3}$.

Bước 1:

Theo công thức hạ bậc ta có: $2{\sin ^2}x=1 - \cos 2x$

=>$y = 2{\sin ^2}x + {\cos ^2}2x$$= 1 - \cos 2x + {\cos ^2}2x$

$=(\cos 2x)^2- \cos 2x +1$

Bước 2:

Đặt $t = \cos 2x;t \in \left[ { - 1;1} \right]$ ta được $y = f\left( t \right) = {t^2} - t + 1;t \in \left[ { - 1;1} \right]$.

Bước 3:

Ta cần tìm GTLN và GTNN của hàm số $f\left( t \right) = {t^2} - t + 1$ trên đoạn $\in \left[ { - 1;1} \right]$.

$\Rightarrow f\left( 1 \right) = 1;f\left( {\dfrac{1}{2}} \right) = \dfrac{3}{4};f\left( { - 1} \right) = 3$

Số lớn nhất là $3$, số nhỏ nhất là $\dfrac{3}{4}$.

$\Rightarrow \max y = 3;\min y = \dfrac{3}{4}$.

Điều kiện: $\cos \left( {2x - \dfrac{\pi }{4}} \right) \ne 0 \Leftrightarrow 2x - \dfrac{\pi }{4} \ne \dfrac{\pi }{2} + k\pi \Leftrightarrow 2x \ne \dfrac{{3\pi }}{4} + k\pi \Leftrightarrow x \ne \dfrac{{3\pi }}{8} + \dfrac{k\pi }{2}$

Điều kiện: $\cos 3x - 1 \ne 0 \Leftrightarrow \cos 3x \ne 1 \Leftrightarrow 3x \ne k2\pi  \Leftrightarrow x \ne \dfrac{{k2\pi }}{3}$

Điều kiện: $\dfrac{{1 - \cos 3x}}{{1 + \sin 4x}} \ge 0$

Nhận thấy $\left\{ \begin{array}{l}\cos 3x \le 1,\forall x \Rightarrow 1 - \cos 3x \ge 0\\\sin 4x \ge  - 1,\forall x \Rightarrow 1 + \sin 4x \ge 0\end{array} \right. \Rightarrow \dfrac{{1 - \cos 3x}}{{1 + \sin 4x}} \ge 0,\forall x$

Do đó hàm số xác định nếu:

$1 + \sin 4x \ne 0 \Leftrightarrow \sin 4x \ne  - 1 \Leftrightarrow 4x \ne  - \dfrac{\pi }{2} + k2\pi  \Leftrightarrow x \ne  - \dfrac{\pi }{8} + k\dfrac{\pi }{2}$

Do $- 1 \le \sin x \le 1 \Rightarrow -2 \le 2\sin x \le 2$$\Rightarrow -2+3 \le2\sin x + 3 \le 2+3$$\Rightarrow1 \le \sqrt {2\sin x + 3}  \le \sqrt 5$.

Dấu “=” xảy ra khi lần lượt $\sin x =  - 1$ và $\sin x = 1$

Bước 1:

Ta có: $y = 3\sin x + 4\cos x - 1$ $\Leftrightarrow y + 1 = 3\sin x + 4\cos x$

$\Rightarrow{\left( {y + 1} \right)^2}= {\left( {3\sin x + 4\cos x} \right)^2}$

Bước 2:

Sử dụng bất đẳng thức Bu – nhi – a Cốp – xki: ${\left( {ac + bd} \right)^2}\le\left( {{a^2} + {b^2}} \right)\left( {{c^2} + {d^2}} \right)$ . Với $a=3, c=\sin x, b=4, d=\cos x$

Khi đó ${\left( {3.\sin x + 4.\cos x} \right)^2} \le \left( {{3^2} + {4^2}} \right)\left( {{{\sin }^2}x + {{\cos }^2}x} \right)$$= \left( {{3^2} + {4^2}} \right).1 = 25$ $\Rightarrow  - 5 \le y + 1 \le 5 \Leftrightarrow  - 6 \le y \le 4$

Bước 3:

Dấu “=” xảy ra $\Leftrightarrow \dfrac{{\sin x}}{3} = \dfrac{{\cos x}}{4}$$\Leftrightarrow \tan x = \dfrac{3}{4}$ $\Leftrightarrow x = \arctan \dfrac{3}{4} + k\pi$

Bước 1:

Ta có

$y = {\sin ^2}x + 3\sin 2x + 3{\cos ^2}x$ $={\sin ^2}x +{\cos ^2}x + 3\sin 2x + 2{\cos ^2}x$ $= 1 + 3\sin 2x + 2{\cos ^2}x$ $= 1 + 3\sin 2x + 1 + \cos 2x$ $= 2 + 3\sin 2x + \cos 2x$

Bước 2:

$\Rightarrow y - 2 = 3\sin 2x + \cos 2x$$\Rightarrow {\left( {y - 2} \right)^2} = {\left( {3\sin 2x + \cos 2x} \right)^2}$ 

Bước 3:

${\left( {3\sin 2x + \cos 2x} \right)^2} = {\left( {3.\sin 2x +1. \cos 2x} \right)^2}$

Áp dụng BĐT Bu-nhi-a Cốp-xki  với $a=3;b=1;c=\sin 2x;d=\cos 2x$${\left( {3.\sin 2x +1. \cos 2x} \right)^2}$ $\le \left( {{3^2} + {1^2}} \right)\left( {{{\sin }^2}2x + {{\cos }^2}2x} \right) = 10.1=10$

$\Rightarrow {\left( {y - 2} \right)^2} \le 10$

$\Rightarrow  - \sqrt {10}  \le y - 2 \le \sqrt {10}$ $\Rightarrow 2 - \sqrt {10}  \le y \le 2 + \sqrt {10}$

Bước 4:

Dấu “=” xảy ra

$\Leftrightarrow \dfrac{{\sin 2x}}{3} = \dfrac{{\cos 2x}}{1}$$\Leftrightarrow \dfrac{{\sin 2x}}{\cos 2x}=3\Leftrightarrow  \tan 2x = 3$ $\Leftrightarrow 2x = \arctan 3 + k\pi$ $\Leftrightarrow x = \dfrac{{\arctan 3}}{2} + \dfrac{{k\pi }}{2}$.

ĐKXĐ: $5\sin 4x - 6\cos 4x + 2m - 1 \ge 0,\forall x$$\Leftrightarrow 2m \ge  - 5\sin 4x + 6\cos 4x + 1,\forall x$

$\Rightarrow 2m \ge \max f\left( x \right)$ với $f\left( x \right) = 6\cos 4x - 5\sin 4x + 1$

$f\left( x \right) = \sqrt {{6^2} + {5^2}} .\left( {\dfrac{6}{{\sqrt {{6^2} + {5^2}} }}.\cos 4x - \dfrac{5}{{\sqrt {{6^2} + {5^2}} }}.\sin 4x} \right)$

$f(x) = \sqrt {61} \left( {\dfrac{6}{{\sqrt {61} }}\cos 4x - \dfrac{5}{{\sqrt {61} }}\sin 4x} \right) + 1 = \sqrt {61} \sin \left( {\alpha  - 4x} \right) + 1$ với $\sin \alpha  = \dfrac{6}{{\sqrt {61} }},\cos \alpha  = \dfrac{5}{{\sqrt {61} }}$.

$\Rightarrow f(x) \le \sqrt {61}  + 1 \Rightarrow \max f(x) = \sqrt {61}  + 1 \Rightarrow m \ge \dfrac{{\sqrt {61}  + 1}}{2}$

Ta có:

$\begin{array}{l}{\left( {2\sin 2x - \cos 2x} \right)^2} \ge \left[ {{2^2} + {{\left( { - 1} \right)}^2}} \right]\left( {{{\sin }^2}2x + {{\cos }^2}2x} \right) = 5\\ \Rightarrow  - \sqrt 5  \le 2\sin 2x - \cos 2x \le \sqrt 5 \\ \Rightarrow 2\sin 2x - \cos 2x + 4 \ge 4 - \sqrt 5  > 0\end{array}$

=> Hàm số luôn xác định trên $\mathbb{R}$

Bước 1:

Ta có $y = \dfrac{{\sin 2x + 2\cos 2x + 3}}{{2\sin 2x - \cos 2x + 4}}$$\Leftrightarrow 2y.\sin 2x - y.\cos 2x + 4y$$= \sin 2x + 2\cos 2x + 3$

$\Leftrightarrow \left( {2y - 1} \right).\sin 2x - \left( {y + 2} \right).\cos 2x = 3 - 4y$

$\Rightarrow [\left( {2y - 1} \right).\sin 2x - \left( {y + 2} \right).\cos 2x]^2 = (3 - 4y)^2$  (*)

Bước 2:

Theo bất đẳng thức Bunhiacopxki, ta có ${\left[ {\left( {2y - 1} \right).\sin 2x - \left( {y + 2} \right).\cos 2x} \right]^2}$

$\le \left[ {{{\left( {2y - 1} \right)}^2} + {{\left( {y + 2} \right)}^2}} \right]\left( {{{\sin }^2}2x + {{\cos }^2}2x} \right)$$= {\left( {2y - 1} \right)^2} + {\left( {y + 2} \right)^2}$

Bước 3:

Kết hợp với (*), ta được ${\left( {3 - 4y} \right)^2} \le {\left( {2y - 1} \right)^2} + {\left( {y + 2} \right)^2}$

$\Leftrightarrow 9 - 24y + 16{y^2}$$\le \left( {4{y^2} - 4y + 1} \right) + \left( {{y^2} + 4y + 4} \right)$

$\Leftrightarrow 16{y^2} - 24y + 9 \le 5{y^2} + 5$

$\Leftrightarrow 11{y^2} - 24y + 4 \le 0$$\Leftrightarrow \dfrac{2}{11} \le y \le 2$

$\Rightarrow\min y = \dfrac{2}{{11}};\max y = 2$

Đặt $t = 3.\sin x + 4.\cos x$, theo bất đẳng thức Bunhiacopxki, ta có:

$\begin{array}{l} {t^2} = {\left( {3\sin x + 4\cos x} \right)^2}\\ \le \left( {{3^2} + {4^2}} \right)\left( {{{\sin }^2}x + {{\cos }^2}x} \right)\\ = 25.1 = 25\\ \Rightarrow {t^2} \le 25 \Rightarrow - 5 \le t \le 5 \end{array}$

Xét hàm số $y = 3{t^2} + 4t + 1$ trên $[-5;5]$.

Hàm số $y = 3{t^2} + 4t + 1$ là hàm bậc hai có:

$\begin{array}{l} - \frac{b}{{2a}} = - \frac{2}{3} \in \left[ { - 5;5} \right]\\ y\left( { - \frac{2}{3}} \right) = - \frac{1}{3}\\ y\left( { - 5} \right) = 56\\ y\left( 5 \right) = 96 \end{array}$

Ta có bảng biến thiên:

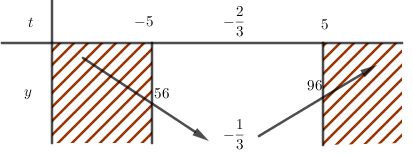
$\Rightarrow \min y =  - \dfrac{1}{3}$ khi $t=- \dfrac{1}{3}$

$\max y = 96$ khi $t=5$.

Đặt $y = \dfrac{{3\sin 2x + \cos 2x}}{{\sin 2x + 4{{\cos }^2}x + 1}}$$= \dfrac{{3\sin 2x + \cos 2x}}{{\sin 2x + 2\left( {1 + \cos 2x} \right) + 1}}$$= \dfrac{{3\sin 2x + \cos 2x}}{{\sin 2x + 2\cos 2x + 3}}$

$\Leftrightarrow y.\sin 2x + 2y.\cos 2x + 3y = 3.\sin 2x + \cos 2x$$\Leftrightarrow \left( {y - 3} \right).\sin 2x + \left( {2y - 1} \right).\cos 2x =  - 3y$  (*)

Theo bất đẳng thức Bunhiacopxki, ta có ${\left[ {\left( {y - 3} \right).\sin 2x + \left( {2y - 1} \right).\cos 2x} \right]^2} \le {\left( {y - 3} \right)^2} + {\left( {2y - 1} \right)^2}$

Kết hợp với (*), ta được $9{y^2} \le \left( {y - 3} \right){\,^2} + {\left( {2y - 1} \right)^2} \Leftrightarrow y \le \dfrac{{ - 5 + \sqrt {65} }}{4}$$\Rightarrow \max y = \dfrac{{ - 5 + \sqrt {65} }}{4}$

Để bất phương trình $y \le m + 1;x \in \mathbb{R}$$\Leftrightarrow m + 1 \ge \max y = \dfrac{{ - 5 + \sqrt {65} }}{4}$$\Leftrightarrow m \ge \dfrac{{\sqrt {65}  - 9}}{4}$

Ta có: $y = \cos 2x + \cos x = 2{\cos ^2}x + \cos x - 1$.

Đặt $\cos {\mkern 1mu} x = t,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} t \in \left[ { - 1;1} \right]$. Hàm số trở thành $y = 2{t^2} + t - 1$. Đây là 1 parabol có bề lõm hướng lên, có hoành độ đỉnh $x =  - \dfrac{b}{{2a}} =  - \dfrac{1}{4}$.

BBT:

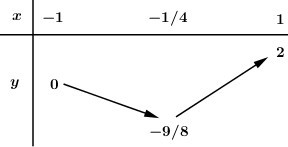
Dựa vào BBT ta có: $M = 2,\,\,m =  - \dfrac{9}{8}$,

Vậy $M + m = 2 - \dfrac{9}{8} = \dfrac{7}{8}$.

Ta vẽ đồ thị hàm số $y = \tan x$ trên đoạn $\left[ {0;5\pi } \right]$.

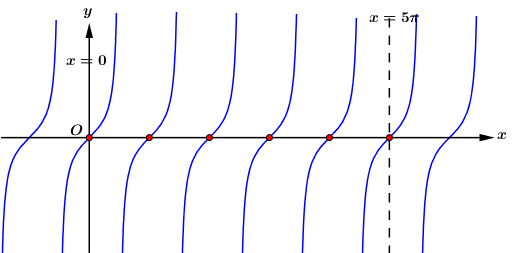
Dựa vào đồ thị hàm số ta thấy trên đoạn $\left[ {0;5\pi } \right]$, đồ thị hàm số cắt trục hoành tại 6 điểm phân biệt (điểm màu đỏ), do đó có 6 giá trị $x \in \left[ {0;5\pi } \right]$ để hàm số $y = \tan x$ nhận giá trị bằng 0.