Câu hỏi:
2 năm trước
Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \cos 2x + \cos x\). Khi đó \(M + m\) bằng bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: d
Ta có: \(y = \cos 2x + \cos x = 2{\cos ^2}x + \cos x - 1\).
Đặt \(\cos {\mkern 1mu} x = t,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} t \in \left[ { - 1;1} \right]\). Hàm số trở thành \(y = 2{t^2} + t - 1\). Đây là 1 parabol có bề lõm hướng lên, có hoành độ đỉnh \(x = - \dfrac{b}{{2a}} = - \dfrac{1}{4}\).
BBT:
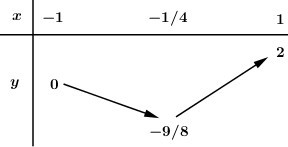
Dựa vào BBT ta có: \(M = 2,\,\,m = - \dfrac{9}{8}\),
Vậy \(M + m = 2 - \dfrac{9}{8} = \dfrac{7}{8}\).
Hướng dẫn giải:
Đặt \(\cos \,x = t,\,\,\,t \in \left[ { - 1;1} \right]\). Tìm GTLN, GTNN của hàm số \(y = f\left( t \right) = 2{t^2} + t - 1\) trên đoạn \(\left[ { - 1;1} \right]\) bằng cách lập BBT.

