Khẳng định nào sau đây là đúng?
Ta có đồ thị hàm số \(y = \left| {\tan x} \right|\) như sau:
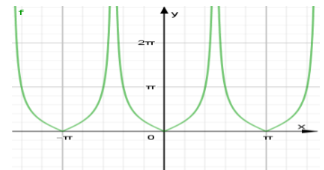
TXĐ: \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
Dựa vào đồ thị hàm số ta thấy:
- Hàm số \(y = \left| {\tan x} \right|\) nghịch biến trên \(\left( { - \dfrac{\pi }{2};0} \right)\) và đồng biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\), do đó đáp án A và D sai.
- Đặt \(f\left( x \right) = \left| {\tan x} \right|\), \(\forall x \in D \Rightarrow - x \in D\).
\(f\left( { - x} \right) = \left| {\tan \left( { - x} \right)} \right| = \left| { - \tan x} \right| = \left| {\tan x} \right| = f\left( x \right)\), do đó hàm số đã cho là hàm chẵn trên tập xác định. Do đó đáp án B đúng.
- Do là hàm chẵn nên đồ thị hàm số đối xứng qua trục Oy chứ không đối xứng qua tâm O, do đó đáp án C sai.
Xét sự biến thiên của hàm số \(y = \sin x - \cos x\). Trong các kết luận sau, kết luận nào đúng?
Ta có: \(\sin x - \cos x = \sqrt 2 \sin \left( {x - \frac{\pi }{4}} \right)\) nên tập giá trị của hàm số là \(\left[ { - \sqrt 2 ;\sqrt 2 } \right]\), do đó loại đáp án C.
Hàm số đã cho tuần hoàn với chu kì \(2\pi \), ta xét sự biến thiên của hàm số trên đoạn \(\left[ { - \dfrac{\pi }{4};\dfrac{{7\pi }}{4}} \right]\).
- Hàm số \(y = \sin x\) đồng biến trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\) nên hàm số \(y = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\) nghịch biến trên \(\left( { - \dfrac{\pi }{4};\dfrac{{3\pi }}{4}} \right)\).
- Hàm số \(y = \sin x\) nghịch biến trên \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\) nên hàm số \(y = \sqrt 2 \sin \left( {x - \dfrac{\pi }{4}} \right)\) nghịch biến trên \(\left( {\dfrac{{3\pi }}{4};\dfrac{{7\pi }}{4}} \right)\).
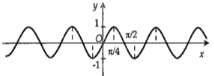
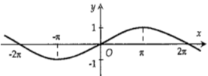
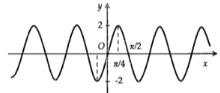
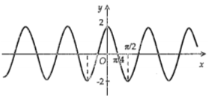
Hình nào dưới đây biểu diễn đồ thị hàm số \(y = f\left( x \right) = 2\sin 2x\).
Ta có: \( - 2 \le 2\sin 2x \le 2\) nên loại đáp án A và B.
Cho \(x = 0 \Rightarrow y = 2\sin 0 = 0\), do đó đồ thị hàm số \(y = f\left( x \right) = 2\sin 2x\) đi qua điểm (0;0). Loại đáp án D.
Xét sự biến thiên của hàm số \(y = 1 - \sin x\) trên một chu kì tuần hoàn của nó. Trong các kết luận sau, kết luận nào sai?
Hàm số đã cho tuần hoàn với chu kì \(2\pi \) và kết hợp với các đáp án ta xét sự biến thiên của hàm số trên đoạn \(\left[ { - \dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right]\).
- Hàm số \(y = \sin x\) đồng biến trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\) nên hàm số \(y = 1 - \sin x\) nghịch biến trên \(\left( { - \dfrac{\pi }{2};\dfrac{\pi }{2}} \right)\).
- Hàm số \(y = \sin x\) nghịch biến trên \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\) nên hàm số \(y = 1 - \sin x\) đồng biến trên \(\left( {\dfrac{\pi }{2};\dfrac{{3\pi }}{2}} \right)\).
Do đó chỉ có đáp án D là sai.
Hàm số nào trong các hàm số sau có đồ thị nhận \(Oy\) làm trục đối xứng ?
Xét đáp án A:
TXĐ: \(D = \mathbb{R}\)\( \Rightarrow \forall x \in D \Rightarrow - x \in D\)
\(\begin{array}{l}y\left( { - x} \right) = \left| { - x} \right|.\sin \left( { - x} \right) = x.\left( { - \sin x} \right)\\ = - x.\sin x = - y\left( x \right)\end{array}\)
=> Đây là hàm số lẻ nên không nhận Oy làm trục đối xứng.
Xét đáp án B:
\(\tan x = \dfrac{{\sin x}}{{\cos x}}\) => ĐKXĐ: \(\cos x \ne 0 \Leftrightarrow x \ne \dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}\)
=> TXĐ: \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,k \in \mathbb{Z}} \right\}\)\( \Rightarrow \forall x \in D \Rightarrow - x \in D\)
\(\begin{array}{l}y\left( { - x} \right) = \sin \left( { - x} \right){\cos ^2}\left( { - x} \right) + \tan \left( { - x} \right)\\ = \left( { - \sin x} \right){\left[ {\cos \left( { - x} \right)} \right]^2} + \left( { - \tan x} \right)\\ = - \sin x.{\left( {\cos x} \right)^2} - \tan x\\= - \sin x{\cos ^2}x - \tan x\\ = - \left( {\sin x.{{\cos }^2}x + \tan x} \right) = - y\left( x \right)\end{array}\)
=> Đây là hàm số lẻ nên không nhận Oy làm trục đối xứng.
Xét đáp án C:
TXĐ: \(D = \mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi ,\,\,k \in \mathbb{Z}} \right\}\)\( \Rightarrow \forall x \in D \Rightarrow - x \in D\).
\(y\left( { - x} \right) = \dfrac{{{{\sin }^{2020}}\left( { - x} \right) + 2019}}{{\cos \left( { - x} \right)}}\)\( = \dfrac{{{{\sin }^{2020}}x + 2019}}{{\cos x}} = y\left( { - x} \right).\)
Do đó hàm số \(y = \dfrac{{{{\sin }^{2020}}x + 2019}}{{\cos x}}\) là hàm số chẵn và nhận trục \(Oy\) làm trục đối xứng.
Xét đáp án D:
Theo lý thuyết về hàm số \(y = \tan x\) thì đây là hàm số lẻ nên không nhận Oy làm trục đối xứng.
Cho các mệnh đề sau :
(I): Hàm số \(y = \sin x\) có chu kì là \(\dfrac{\pi }{2}\).
(II): Hàm số \(y = \tan x\) có tập giá trị là \(\mathbb{R}\backslash \left\{ {\dfrac{\pi }{2} + k\pi |k \in {\rm Z}} \right\}\)
(III): Đồ thị hàm số \(y = \cos x\) đối xứng qua trục tung.
(IV): Hàm số \(y = \cot x\) nghịch biến trên \(\left( { - \pi ;0} \right)\)
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên ?
(I): Hàm số \(y = \sin x\) có chu kỳ là \(2\pi \) nên I sai.
(II): Hàm số \(y = \tan x\) có tập giá trị là \(\mathbb{R}\) nên II sai.
Tập hợp bài đưa ra là tập xác định của hàm số.
(III): Ta có hàm số \(y = \cos x\) có
$y(-x)=\cos (-x)=\cos x=y(x)$
=> \(y\left( x \right) = y\left( { - x} \right)\) nên đồ thị hàm số đối xứng với nhau qua trục tung nên III đúng.
(IV): Hàm số \(y = \cot x\) luôn nghịch biến trên \(\left( {k\pi ;\pi + k\pi } \right)\)
Với $k=-1$ thì hàm số nghịch biến trên \(\left( {-\pi;0 } \right)\) nên IV đúng.
Giá trị nhỏ nhất của hàm số \(y = 2{\cos ^2}x + \sin 2x\) là
Bước 1:
Ta có \(y = 2{\cos ^2}x + \sin 2x = 2.\dfrac{{1 + \cos 2x}}{2} + \sin 2x\)\( = 1 + \cos 2x + \sin 2x\)
Bước 2:
\( \Rightarrow \dfrac{y}{{\sqrt 2 }} = \dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }}\cos 2x + \dfrac{1}{{\sqrt 2 }}\sin 2x\) \( = \dfrac{1}{{\sqrt 2 }} + \cos 2x\cos \dfrac{\pi }{4} + \sin 2x.\sin \dfrac{\pi }{4}\) \( = \dfrac{1}{{\sqrt 2 }} + \cos \left( {2x - \dfrac{\pi }{4}} \right)\)
Bước 3:
Ta có \(\cos \left( {2x - \dfrac{\pi }{4}} \right) \ge - 1 \Leftrightarrow \dfrac{1}{{\sqrt 2 }} + \cos \left( {2x - \dfrac{\pi }{4}} \right) \ge - 1 + \dfrac{1}{{\sqrt 2 }}\)
Hay \(\dfrac{y}{{\sqrt 2 }} \ge - 1 + \dfrac{1}{{\sqrt 2 }} \Leftrightarrow y \ge 1 - \sqrt 2 \)
Bước 4:
Dấu = xảy ra khi \(\cos \left( {2x - \dfrac{\pi }{4}} \right) = - 1 \Leftrightarrow 2x - \dfrac{\pi }{4} = - \pi + k2\pi \Leftrightarrow x = \dfrac{{ - 3\pi }}{8} + k\pi \,\,\left( {k \in \mathbb{Z}} \right)\)
Bước 5:
Vậy giá trị nhỏ nhất của \(y\) là \(1 - \sqrt 2 \).
Tìm m để hàm số \(y = \sqrt {8\cos x - 6\sin x - {{\left( {3\sin x - 4\cos x} \right)}^2} - 2m} \) có tập xác định là R.
Bước 1:
Ta có \(y = \sqrt {8\cos x - 6\sin x - {{\left( {3\sin x - 4\cos x} \right)}^2} - 2m} \)
Hàm số trên có tập xác định R khi
\(\begin{array}{l}8\cos x - 6\sin x - {\left( {3\sin x - 4\cos x} \right)^2} - 2m \ge 0\\ \Leftrightarrow 2\left( {4\cos x - 3\sin x} \right) - {\left( {3\sin x - 4\cos x} \right)^2} - 2m \ge 0\end{array}\)
Bước 2:
Đặt \(t = 4\cos x - 3\sin x\)
Theo BĐT Bu-nhi-a-cốp-xki ta có:
\({t^2} = {\left( {4\cos x - 3\sin x} \right)^2}\)\( \le \left( {{4^2} + {3^2}} \right)\left( {{{\sin }^2}x + {{\cos }^2}x} \right) = 25\)\( \Leftrightarrow - 5 \le t \le 5\)
Bước 3:
Ta có bất phương trình \(2t - {t^2} - 2m \ge 0\forall t \in \left[ { - 5;5} \right]\)
\( \Leftrightarrow - 2m \ge {t^2} - 2t\forall t \in \left[ { - 5;5} \right]\)(1)
Bước 4:
Xét hàm số \(f\left( t \right) = {t^2} - 2t\) trên \(\left[ { - 5;5} \right]\)
Ta có $-\dfrac{b}{2a}=1 \in \left[ { - 5;5} \right]$
Vì $a=1>0$ nên hàm số nghịch biến trên $(-\infty;1)$ và đồng biến trên $(1;+\infty)$
Mà $(-5;1) \subset (-\infty;1)$ và $(1;5) \subset (1;+\infty)$ nên hàm số nghịch biến trên $(-5;1)$ và đồng biến trên $(1;5)$.
Bảng biến thiên:
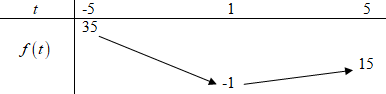
Bước 5:
Dựa vào bảng biến thiên ta thấy bất đẳng thức (1) xảy ra khi \( - 2m \ge 35 \Leftrightarrow m \le - \dfrac{{35}}{2}\)
Cho hàm số lượng giác \(f(x) = \tan x - \dfrac{1}{{\sin x}}\).
Xét tính tuần hoàn và tìm chu kì (nếu có) của hàm số trên.
Bước 1: Tìm điều kiện xác định của hàm số \(f(x) = \tan x - \dfrac{1}{{\sin x}}\)
Điều kiện xác định \(\left\{ {\begin{array}{*{20}{l}}{\cos x \ne 0}\\{\sin x \ne 0}\end{array} \Leftrightarrow x \ne k\dfrac{\pi }{2} \Rightarrow D = \mathbb{R}\backslash \left\{ {k\dfrac{\pi }{2}} \right\}} \right.\).
Bước 2: Chu kì của hàm số \(y = \tan x\) và \(g(x) = \dfrac{1}{{\sin x}}\)
Xét hàm số \(y = \tan x\) là hàm tuần hoàn có chu kì \({T_1} = \pi \).
Xét hàm số \(g(x) = \dfrac{1}{{\sin x}}\).
Ta có \(g\left( {x + {T_2}} \right) = g(x) \Leftrightarrow \dfrac{1}{{\sin \left( {x + {T_2}} \right)}} = \dfrac{1}{{\sin x}} \Leftrightarrow \sin \left( {x + {T_2}} \right) = \sin x\).
Chọn \(x = \dfrac{\pi }{2} \Rightarrow \sin x = 1\)
\( \Rightarrow \sin \left( {\dfrac{\pi }{2} + {T_2}} \right) = 1 \Leftrightarrow \dfrac{\pi }{2} + {T_2} = \dfrac{\pi }{2} + k2\pi (k \in \mathbb{Z}) \Leftrightarrow {T_2} = k2\pi (k \in \mathbb{Z}).\)
Giá trị nhỏ nhất của \({T_2}\) là \(2\pi \).
Ta thấy \(\forall x \in D;x + k2\pi \in D\) thì \(g(x + k2\pi ) = g(x)\).
Vậy hàm số \(g(x) = \dfrac{1}{{\sin x}}\) là hàm số tuần hoàn với chu kì \({T_2} = 2\pi \).
Bước 3: Chu kì của hàm số \(f(x) = \tan x - \dfrac{1}{{\sin x}}\)
Khi đó, hàm số \(y = \tan x - \dfrac{1}{{\sin x}}\) là hàm tuần hoàn với chu kì \(T = 2\pi \).
Cho hàm số lượng giác \(f(x) = \tan x - \dfrac{1}{{\sin x}}\).
Xét tính chẵn, lẻ của hàm số trên.
Bước 1: Chứng tỏ \(\forall x \in D \Rightarrow - x \in D\)
Ta thấy \(\forall x \in D \Rightarrow - x \in D\).
Bước 2: Tính \(f( - x)\) và kết luận
Mặt khác, \(f( - x) = \tan ( - x) - \dfrac{1}{{\sin ( - x)}}\)\( = - \tan x + \dfrac{1}{{\sin x}} = - f(x)\)
\( \Rightarrow \) Hàm số \(f(x) = \tan x - \dfrac{1}{{\sin x}}\) là hàm lẻ.