Câu hỏi:
1 năm trước
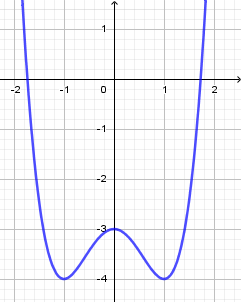
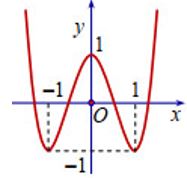
Biết rằng hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị là đường cong như hình vẽ bên dưới.
Tính giá trị \(f\left( {3a + 2b + c} \right)\).
Trả lời bởi giáo viên
Đáp án đúng: a
Ta có \(f'\left( x \right) = 4a{x^3} + 2bx\).
Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số đi qua các điểm \(\left( {0;1} \right);\,\,\left( {1; - 1} \right)\).
Đồng thời đây cũng là 2 điểm cực trị của hàm số. Do đó ta có hệ phương trình:
\(\left\{ \begin{array}{l}f\left( 0 \right) = 1\\f\left( 1 \right) = - 1\\f'\left( 1 \right) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a + b + c = - 1\\4a + 2b = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 1\\a = 2\\b =- 4\end{array} \right.\).
\( \Rightarrow f\left( x \right) = 2{x^4} - 4{x^2} + 1\) và \(3a + 2b + c = 3.2 + 2.(-4) + 1 = -1\).
Vậy \(f\left( {3a + 2b + c} \right) = f\left( -1 \right) = - 1\).
Hướng dẫn giải:
- Dựa vào các điểm mà đồ thị hàm số đi qua và các điểm cực trị của đồ thị hàm số, tìm giá trị của \(a,\,\,b,\,\,c\).
- Suy ra hàm số. Tính \(3a + 2b + c\), từ đó tính \(f\left( {3a + 2b + c} \right)\).
Câu hỏi khác
- Bài tập phần giá trị lớn nhất và giá trị nhỏ nhất của hàm số thi ĐGTD Bách khoa
- Bài tập phần sự đồng biến, nghịch biến của hàm số thi ĐGTD Bách khoa
- Bài tập phần đường tiệm cận của đồ thị hàm số thi ĐGTD Bách khoa
- Bài tập phần bài toán cực trị có tham số đối với một số hàm số cơ bản thi ĐGTD Bách khoa
- Bài tập phần cực trị của hàm số thi ĐGTD Bách khoa
